《機械》〈自動制御〉[H23:問7]フィードバック制御系の設計仕様を与える尺度に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，フィードバック制御系の設計仕様を与える尺度に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

フィードバック制御系の設計仕様には，周波数領域及び時間領域における尺度がある。前者の周波数領域における設計においては，$ \ \fbox {　（１）　} \ $の仕様を与える尺度としてゲイン余裕や位相余裕があり，また，$ \ \fbox {　（２）　} \ $の仕様を与える尺度としてゲイン交差角周波数や位相交差角周波数がある。これらは開ループ周波数特性に着目した尺度として利用されている。

例えば，開ループ（一巡）伝達関数が$ \ \displaystyle G\left( s\right) = \frac {K}{s\left( Ts+1\right) } \ $で与えられる場合，ゲイン交差角周波数を$ \ 1 \ \mathrm {[rad / s]} \ $に，位相余裕を$ \ 45 \ \mathrm {[°]} \ $に設定するには，$ \ K= \ \fbox {　（３）　} \ $，$ \ T= \ \fbox {　（４）　} \ \mathrm {[s]} \ $に選べばよい。

一方，閉ループ周波数特性に着目した場合には，$ \ \fbox {　（１）　} \ $の尺度としてピーク値（共振値），$ \ \fbox {　（２）　} \ $の尺度として$ \ \fbox {　（５）　} \ $などが利用されている。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　帯域幅　　　　　&（ロ）&　\frac {1}{2}　　　　　&（ハ）&　\sqrt {2} \\[ 5pt ] &（ニ）&　定常特性　　　　　&（ホ）&　\frac {1}{4}　　　　　&（ヘ）&　1 \\[ 5pt ] &（ト）&　外乱抑制特性　　　　　　　&（チ）&　速応性　　　　　&（リ）&　低感度特性 \\[ 5pt ] &（ヌ）&　最適性　　　　　&（ル）&　\frac {1}{\sqrt {2}}　　　　　&（ヲ）&　2 \\[ 5pt ] &（ワ）&　安定性　　　　　&（カ）&　整定時間　　　　　&（ヨ）&　オーバーシュート量 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

自動制御の設計に関する問題です。
電験で出題されるのは主に安定性で，速応性に関する問題は稀かと思います。
したがって，本問においては(1)，(3)，(4)をしっかり理解しておきたい問題となります。

1.システムの安定性と速応性
システムの安定性と速応性は，読んで字のごとくどれだけシステムが安定しているか，どれだけ速く応答するかの指標です。ゲイン余裕や位相余裕，ゲイン交差角周波数や位相交差角周波数は，開ループ周波数伝達関数を用いたボード線図とナイキスト線図により理解することができます。
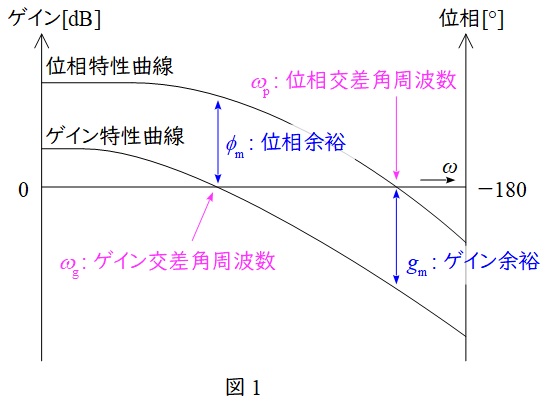
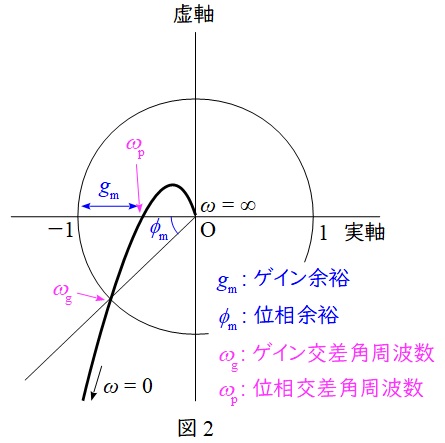
ボード線図は，横軸に角周波数，縦軸にゲインと位相の二軸としたグラフで図1のように描くことができ，ナイキスト線図は実軸と虚軸の平面において，角周波数を$ \ 0 \ $から$ \ \infty \ $まで変化させたときのベクトル軌跡で図2のように描くことができます。
安定性の仕様を与える尺度としてはゲイン余裕$ \ g_{\mathrm {m}} \ $と位相余裕$ \ \phi _{\mathrm {m}} \ $があり，ゲイン余裕は位相が$ \ -180 \ [°] \ $のときの$ \ 0 \ \mathrm {[dB]} \ $との差で，位相余裕はゲインが$ \ 0 \ \mathrm {[dB]} \ $のときの$ \ -180 \ [°] \ $との位相差となります。ボード線図とナイキスト線図においては図1及び図2に示すような相互関係になります。
速応性の仕様を与える尺度としてはゲイン交差角周波数$ \ \omega _{\mathrm {g}} \ $と位相交差角周波数$ \ \omega _{\mathrm {p}} \ $があり，ゲイン交差角周波数はゲインが$ \ 0 \ \mathrm {[dB]} \ $のときの角周波数，位相交差角周波数は位相が$ \ -180 \ [°] \ $のときの角周波数となります。ボード線図とナイキスト線図においては図1及び図2に示すような相互関係になります。

【解答】

(1)解答：ワ
題意より解答候補は，（ニ）定常特性，（ト）外乱抑制特性，（チ）速応性，（リ）低感度特性，（ヌ）最適性，（ワ）安定性，等になると思います。
ワンポイント解説「1.システムの安定性と速応性」の通り，ゲイン余裕や位相余裕は安定性の仕様を与える尺度となります。ナイキストの安定判別法は1種令和2年機械制御問4に具体的に出題されているので，理解しておいた方が良いかと思います。

(2)解答：チ
題意より解答候補は，（ニ）定常特性，（ト）外乱抑制特性，（チ）速応性，（リ）低感度特性，（ヌ）最適性，（ワ）安定性，等になると思います。
ワンポイント解説「1.システムの安定性と速応性」の通り，ゲイン交差角周波数や位相交差角周波数は速応性の仕様を与える尺度となります。例えば，ゲイン交差角周波数が大きければ，速応性が高い制御ということになります。

(3)解答：ハ
(4)解答：ヘ
開ループ（一巡）伝達関数が$ \ \displaystyle G\left( s\right) = \frac {K}{s\left( Ts+1\right) } \ $であるとき，周波数伝達関数$ \ G \left( \mathrm {j}\omega \right) \ $は，
\[
\begin{eqnarray}
G \left( \mathrm {j}\omega \right) &=&\frac {K}{\mathrm {j}\omega \left( \mathrm {j}\omega T+1\right) } \\[ 5pt ] &=&\frac {K}{\omega \left( -\omega T+\mathrm {j}\right) } \\[ 5pt ] &=&\frac {K}{\omega \left\{ \left( \omega T\right) ^{2}-1\right\} }\left( -\omega T-\mathrm {j}\right) \\[ 5pt ] &=&\frac {K}{\omega \left\{ 1-\left( \omega T\right) ^{2}\right\} }\left( \omega T+\mathrm {j}\right) \\[ 5pt ] \end{eqnarray}
\] となり，これよりゲイン$ \ g=20\log _{10} \left| G \left( \mathrm {j}\omega \right) \right| \ $と位相余裕$ \ \phi _{\mathrm {m}} \ $は，
\[
\begin{eqnarray}
g &=&20\log _{10}\left| G \left( \mathrm {j}\omega \right) \right| \\[ 5pt ] &=&20\log _{10}\left| \frac {K}{\omega \left( -\omega T+\mathrm {j}\right) } \right| \\[ 5pt ] &=&20\log _{10}\frac {K}{\omega \sqrt {1+\left( \omega T\right) ^{2}} } \\[ 5pt ] \phi _{\mathrm {m}} &=&\tan ^{-1}\frac {1}{\omega T} \\[ 5pt ] \end{eqnarray}
\] となる。ゲイン交差角周波数を$ \ 1 \ \mathrm {[rad / s]} \ $，位相余裕を$ \ 45 \ \mathrm {[°]} \ $に設定するための$ \ T \ $は，
\[
\begin{eqnarray}
\phi _{\mathrm {m}} &=&\tan ^{-1}\frac {1}{\omega T} \\[ 5pt ] 45\mathrm {°} &=&\tan ^{-1}\frac {1}{T} \\[ 5pt ] \frac {1}{T}&=&\tan 45\mathrm {°} \\[ 5pt ] \frac {1}{T}&=&1 \\[ 5pt ] T&=&1 \\[ 5pt ] \end{eqnarray}
\] と求められる。また，ゲイン交差角周波数を$ \ 1 \ \mathrm {[rad / s]} \ $，位相余裕を$ \ 45 \ \mathrm {[°]} \ $に設定するための$ \ K \ $は，
\[
\begin{eqnarray}
g &=&20\log _{10}\frac {K}{\omega \sqrt {1+\left( \omega T\right) ^{2}} } \\[ 5pt ] 0 &=&20\log _{10}\frac {K}{1\times \sqrt {1+\left( 1\times 1\right) ^{2}} } \\[ 5pt ] 0 &=&20\log _{10}\frac {K}{ \sqrt {2} } \\[ 5pt ] \frac {K}{ \sqrt {2} } &=&1 \\[ 5pt ] K &=&\sqrt {2} \\[ 5pt ] \end{eqnarray}
\] と求められる。