Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,論理演算をする論理回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
論理回路を論理的な機能の点から分類すると,現在の入力だけで出力が決まる\( \ \fbox { (1) } \ \)と,現在の入力及び過去の入力系列で出力が決まる順序回路に大別できる。
前者には,論理和\( \ \left( \mathrm {OR}\right) \ \),論理積\( \ \left( \mathrm {AND}\right) \ \),否定\( \ \left( \mathrm {NOT}\right) \ \)などの基本論理回路や,切換回路(マルチプレクサー)などがある。
後者には,双安定マルチバイブレータとも呼ばれ,二つの安定状態を記憶する順序回路であって,入力が与えられると他の安定状態に遷移できる機能をもつ各種の\( \ \fbox { (2) } \ \)や,それを使用したレジスタ回路,カウンタ回路などがある。
また,このような論理回路が搭載される集積回路\( \ \left( \mathrm {IC}\right) \ \)は,汎用論理\( \ \mathrm {IC} \ \)と特定用途向け\( \ \mathrm {IC} \ \)に分類される。
汎用論理\( \ \mathrm {IC} \ \)の一つである\( \ \mathrm {MPU\left( Micro \ Processor \ Unit\right) } \ \)は,記述されたプログラムをシーケンシャルに命令実行処理を必要とする\( \ \fbox { (3) } \ \)に用いられている。
一方,後者の\( \ \mathrm {IC} \ \)として,ある特定用途の論理回路演算を実行処理する複数の回路で構成した集積回路である\( \ \fbox { (4) } \ \)は,最近,多くのディジタル電子機器に用いられている。この特定用途向け\( \ \mathrm {IC} \ \)の設計では,複雑な論理式を簡略化する圧縮が重要である。圧縮法としては,計算機による機械的なアルゴリズム処理が容易な\( \ \fbox { (5) } \ \)が著名であり,複数入力・複数出力のブール関数を簡単化することができる。
〔問8の解答群〕
\[
\begin{eqnarray}
&(イ)& 量子コンピュータ &(ロ)& \mathrm {ASIC\left( Application \ Specific \ Integrated \ Circuit\right) } \\[ 5pt ]
&(ハ)& ニューロコンピュータ &(ニ)& コレスキー法 \\[ 5pt ]
&(ホ)& フリップフロップ &(ヘ)& クワイン・マクラスキー法 \\[ 5pt ]
&(ト)& 論理和否定 &(チ)& 計算回路 \\[ 5pt ]
&(リ)& 解析回路 &(ヌ)& ノイマン形コンピュータ \\[ 5pt ]
&(ル)& カルノー図法 &(ヲ)& \mathrm {DSIC\left( Dedicated \ Specific \ Integrated \ Circuit\right) } \\[ 5pt ]
&(ワ)& 排他的論理和 &(カ)& \mathrm {PSIC\left( Preset \ Specific \ Integrated \ Circuit\right) } \\[ 5pt ]
&(ヨ)& 組合せ回路 && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
情報分野における論理演算の発展的な内容の問題です。
大学等ではフリップフロップや順序回路等を勉強することはありますが,電験ではその回路の詳細や真理値表等は出題されません。
出題されても選択問題なので,本問の内容を知らない方は飛ばしても良いかと思います。
1.組合せ回路と順序回路
組合せ回路は\( \ \mathrm {AND} \ \)や\( \ \mathrm {OR} \ \)といった現在の入力により出力が決まる回路,順序回路はフリップフロップ等のように現在の入力と過去の入力により出力が決まる回路をいいます。
2.フリップフロップ
図1に示すような\( \ \mathrm {RS} \ \)型フリップフロップをはじめとする出力を一時的に保持することができる記憶回路のことをいい,順序回路に分類されます。
真理値表は表1のようになります。
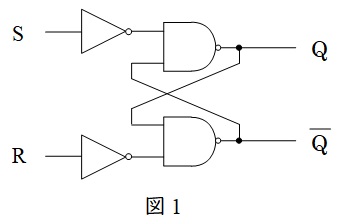
表 1
\[
\begin{array}{|c|c|c|c|}
\hline
\mathrm {S} & \mathrm {R} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 0 & 保持 & 保持 \\
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0 \\
1 & 1 & 禁止 & 禁止 \\
\hline
\end{array}
\]
【解答】
(1)解答:ヨ
題意より解答候補は,(チ)計算回路,(リ)解析回路,(ヨ)組合せ回路,になると思います。
ワンポイント解説「1.組合せ回路と順序回路」の通り,論理回路を論理的な機能の点から分類したとき,現在の入力だけで出力が決まる回路を組合せ回路といいます。
(2)解答:ホ
題意より解答候補は,(ホ)フリップフロップ,(ト)論理和否定,(ワ)排他的論理和,になると思います。
ワンポイント解説「2.フリップフロップ」の通り,順序回路に分類されるのはフリップフロップのみで論理和否定(否定論理和)\( \ \left( \mathrm {NOR}\right) \ \)や排他的論理和\( \ \left( \mathrm {XOR}\right) \ \)は組合せ回路に分類されます。
(3)解答:ヌ
題意より解答候補は,(イ)量子コンピュータ,(ハ)ニューロコンピュータ,(ヌ)ノイマン形コンピュータ,になると思います。
\( \ \mathrm {MPU\left( Micro \ Processor \ Unit\right) } \ \)は\( \ \mathrm {CPU\left( Central \ Processor \ Unit\right) } \ \)と一般的に呼ばれ,現在のコンピュータの前身となっているノイマン形コンピュータに用いられています。
(4)解答:ロ
題意より解答候補は,(ロ)\( \ \mathrm {ASIC\left( Application \ Specific \ Integrated \ Circuit\right) } \ \),(ヲ)\( \ \mathrm {DSIC\left( Dedicated \ Specific \ Integrated \ Circuit\right) } \ \),(カ)\( \ \mathrm {PSIC\left( Preset \ Specific \ Integrated \ Circuit\right) } \ \),になると思います。
ある特定用途の論理回路演算を実行する複数機能の回路を1つにまとめた集積回路は\( \ \mathrm {ASIC\left( Application \ Specific \ Integrated \ Circuit\right) } \ \)と呼ばれます。\( \ \mathrm {DSIC\left( Dedicated \ Specific \ Integrated \ Circuit\right) } \ \)と\( \ \mathrm {PSIC\left( Preset \ Specific \ Integrated \ Circuit\right) } \ \)は聞いたことがありませんので,恐らく知識として不要かと思います。
(5)解答:ヘ
題意より解答候補は,(ニ)コレスキー法,(ヘ)クワイン・マクラスキー法,(ル)カルノー図法,になると思います。
ブール代数を簡略化する方法としてはクワイン・マクラスキー法とカルノー図法がありますが,計算機による処理が向いているのはクワイン・マクラスキー法です。コレスキー法は数学の線形代数で用いる手法の一つですが,電験では不要です。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは