《機械》〈回転機〉[H24:問1]三相誘導電動機の滑りに関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，三相誘導電動機の滑りを$ \ s \ $とするとき，三つの領域$ \ s＜0 \ $，$ \ 0＜s＜1 \ $，$ \ s＞1 \ $における電動機の動作に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

$ \ 0＜s＜1 \ $の領域は通常の誘導電動機動作で，回転子は回転磁界と同方向に同期速度以下で回転し，発生トルクは正である。

$ \ s＜0 \ $の領域では，回転子は回転磁界と同方向に同期速度以上で回転する。したがって，入力は$ \ \fbox {　（１）　} \ $であり，トルクは回転方向と反対方向となるので，電動機運転では制動トルクとなる。このため回転体の運動エネルギーを吸収して電源に電力として返還されるので，効率よく制動できる。これを回生制動という。巻上機，クレーンなどで重量物を降下させる場合に使用される。また，この領域では誘導発電機として動作するが，$ \ \fbox {　（２）　} \ $を必要とするため単独では発電できない。系統と連系する場合，機械的入力が変動しても商用周波数の電力が得られる。構造が簡単で低コストであるかご形誘導発電機が風力発電に広く用いられてきた。かご形誘導発電機は一次端子電圧が一定ならば，その$ \ \fbox {　（３）　} \ $だけで出力が決まるため，風速の変動によって出力が変動する。

$ \ s＞1 \ $の領域では，回転子が回転磁界と反対方向に回転する。発生トルクは正であるが回転子の回転方向と反対であるため，機械的出力は負となる。これを$ \ \fbox {　（４）　} \ $といい，重量物の低速度巻下ろしなどに利用される。機械的出力は負であるから，動力は外部から供給され，この動力及び一次側から供給される入力は主として$ \ \fbox {　（５）　} \ $で熱として消費される。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　鉄損抵抗　　　　　&（ロ）&　滑　り　　　　　&（ハ）&　発電ブレーキ \\[ 5pt ] &（ニ）&　零　　　　　&（ホ）&　始動電流　　　　　&（ヘ）&　標準抵抗 \\[ 5pt ] &（ト）&　励磁電流　　　　　&（チ）&　単相ブレーキ　　　　　　&（リ）&　誘導ブレーキ \\[ 5pt ] &（ヌ）&　定格速度　　　　　&（ル）&　同期速度　　　　　&（ヲ）&　負 \\[ 5pt ] &（ワ）&　定格電流　　　　　&（カ）&　二次抵抗　　　　　&（ヨ）&　正 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘導電動機の滑りの変化に対する動作に違いを問う問題です。出力と滑りの関係や制動なのか運転なのか等よく理解しておくようにしましょう。

1.誘導機の滑り$ \ s \ $
誘導機の同期速度が$ \ N_{\mathrm {s}} \ $，回転数が$ \ N \ $である時，誘導機の滑り$ \ s \ $は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となるので$ \ N \ $について整理すると，
\[
\begin{eqnarray}
s N_{\mathrm {s}}&=&N_{\mathrm {s}}-N \\[ 5pt ] N&=&\left( 1-s\right) N_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.滑りの違いよる電動機の動作の違い
①$ \ s＜0 \ $のとき
$ \ N＞N_{\mathrm {s}} \ $となるので，同期速度$ \ N_{\mathrm {s}} \ $よりも回転数$ \ N \ $が高い状態で，どちらも同方向に回転している状態です。このとき，誘導機は誘導発電機として働き，回生制動となり電源側に電力が返還されます。

②$ \ 0＜s＜1 \ $のとき
$ \ N＜N_{\mathrm {s}} \ $となるので，同期速度$ \ N_{\mathrm {s}} \ $よりも回転数$ \ N \ $が低い状態で，どちらも同方向に回転している状態です。このとき，誘導機は誘導電動機として働き，電源から電力が供給されます。

③$ \ s＞1 \ $のとき
回転数$ \ N \ $に対し同期速度$ \ N_{\mathrm {s}} \ $が逆向きに回転している状態で，このとき逆向きに大きなトルクがかかります。このとき，誘導機は誘導ブレーキとして働き，入力は熱として消費されます。回生制動より大きなトルクがかかるので，急ブレーキとして使用します。

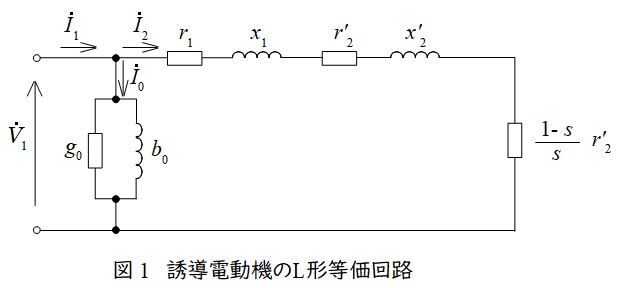
3.誘導電動機のL形等価回路とその特性
誘導電動機のL形等価回路は図1のようになります。図1において，$ \ {\dot V}_{1} \ $は一次側端子電圧，$ \ {\dot I}_{1} \ $は一次電流，$ \ {\dot I}_{2} \ $は二次電流，$ \ {\dot I}_{0} \ $は励磁電流，$ \ r_{1} \ $は一次巻線抵抗，$ \ r_{2}^{\prime } \ $は二次巻線抵抗の一次換算，$ \ x_{1} \ $は一次漏れリアクタンス，$ \ x_{2}^{\prime } \ $は二次漏れリアクタンスの一次換算，$ \ s \ $は滑りとなります。
図1より，出力$ \ P_{\mathrm {o}} \ $，二次銅損$ \ P_{\mathrm {c2}} \ $，二次入力$ \ P_{2} \ $は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& 3r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機に発生するトルク$ \ T \ $は，
\[
\begin{eqnarray}
T &=& \frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=& \frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ] &=& 3\frac {r_{2}^{\prime }}{\omega _{\mathrm {s}}s}I_{2}^{2} \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

【解答】

(1)解答：ヲ
題意より解答候補は，（ニ）零，（ヲ）負，（ヨ）正，になると思います。ワンポイント解説「2.滑りの違いよる電動機の動作の違い」の通り，$ \ s＜0 \ $のとき誘導機は誘導発電機として働くので，電力は電源側に返還されます。すなわち，入力としては負の値となります。

(2)解答：ト
題意より解答候補は，（ホ）始動電流，（ト）励磁電流，（ワ）定格電流，になると思います。
図１の等価回路からもわかる通り，誘導機は負荷電流を流す巻線が励磁電流を流す巻線を兼用しているため，単独で界磁を発生させることができません。したがって，励磁電流は電力系統から供給を受ける必要があり，単独で発電することはできません。

(3)解答：ロ
題意より解答候補は，（イ）鉄損抵抗，（ロ）滑り，（ヘ）標準抵抗，（カ）二次抵抗，になると思います。ワンポイント解説「3.誘導電動機のL形等価回路とその特性」より，出力$ \ P_{\mathrm {o}} \ $は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] \end{eqnarray}
\] となります。ここで，かご形誘導発電機は二次抵抗を変化させることができない（巻線形は可能）ので，二次抵抗$ \ r_{2} \ $は一定であり，等価回路より一次電圧が一定であれば，二次電流も一定となる。したがって，出力は滑り$ \ s \ $だけで決まることになる。

(4)解答：リ
題意より解答候補は，（ハ）発電ブレーキ，（チ）単相ブレーキ，（リ）誘導ブレーキ，になると思います。$ \ s＞1 \ $の領域におけるブレーキの名称は誘導ブレーキとなります。発電ブレーキは$ \ s＜0 \ $の領域となります。

(5)解答：カ
題意より解答候補は，（イ）鉄損抵抗，（ヘ）標準抵抗，（カ）二次抵抗，になると思います。入力が熱として消費されるのは主に二次抵抗となります。