《機械》〈自動制御〉[H25:問6]フィードバック制御系に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，図のフィードバック制御系に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

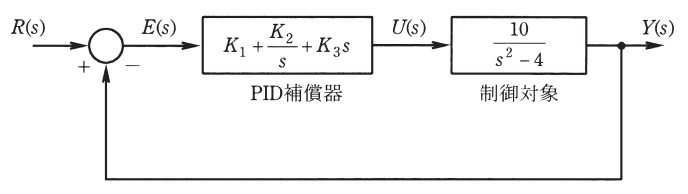
図において，$ \ R(s) \ $は目標値，$ \ E(s) \ $は偏差，$ \ U(s) \ $は操作量，$ \ Y(s) \ $は出力を表し，時間信号$ \ r(t) \ $，$ \ e(t) \ $，$ \ u(t) \ $，$ \ y(t) \ $をそれぞれラプラス変換したものである。この制御対象は，$ \ \fbox {　（１）　} \ $な特性をもつ。この制御対象に対して，パラメータ$ \ K_{1} \ $，$ \ K_{2} \ $，$ \ K_{3} \ $をもつ図の$ \ \mathrm {PID} \ $補償器によってフィードバック制御を行う。このとき，$ \ \mathrm {PID} \ $補償器の積分時間は$ \ \fbox {　（２）　} \ $で与えられる。

$ \ R(s) \ $から$ \ Y(s) \ $までの閉ループ伝達関数の望ましい極が，$ \ -30 \ $，$ \ -3±\mathrm {j}4 \ $になるように補償器のパラメータを求めると，$ \ K_{1}=\fbox {　（３）　} \ $，$ \ K_{2}=75 \ $，$ \ K_{3}=\fbox {　（４）　} \ $となる。このとき，閉ループ伝達関数は三次系となるが，$ \ R(s) \ $から$ \ Y(s) \ $までの応答は，$ \ -3±\mathrm {j}4 \ $を$ \ \fbox {　（５）　} \ $とする二次系の応答に近似できる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　閉ループ極　　　　　&（ロ）&　代表根　　　　　&（ハ）&　14.9 \\[ 5pt ] &（ニ）&　不安定　　　　　&（ホ）&　\frac {K_{2}}{K_{1}}　　　　　&（ヘ）&　1.5 \\[ 5pt ] &（ト）&　漸近安定　　　　　&（チ）&　K_{2}　　　　　&（リ）&　25.9 \\[ 5pt ] &（ヌ）&　2.6　　　　　&（ル）&　20.9　　　　　&（ヲ）&　3.6 \\[ 5pt ] &（ワ）&　\frac {K_{1}}{K_{2}}　　　　　&（カ）&　安　定　　　　　&（ヨ）&　補償極 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

自動制御は二次試験で出題されやすいので，一次試験では出題されにくい分野です。８月時点で二次試験対策をしていた受験生には易しい問題であったかもしれません。

1.$ \ \mathrm {PID} \ $制御
比例動作($ \ \mathrm {P} \ $制御)，積分動作($ \ \mathrm {I} \ $制御)，微分動作($ \ \mathrm {D} \ $制御)を用いた制御を言い，伝達関数$ \ G(s) \ $は，比例ゲイン$ \ K_{\mathrm {p}} \ $，積分時間$ \ T_{\mathrm {I}} \ $，微分時間$ \ T_{\mathrm {D}} \ $を用いて，
\[
\begin{eqnarray}
G(s)&=&K_{\mathrm {p}}\left( 1+\frac {1}{T_{\mathrm {I}}s}+T_{\mathrm {D}}s\right) \\[ 5pt ] \end{eqnarray}
\] で与えられます。

2.特性方程式による安定判別
$ \ \displaystyle W(s)=\frac {G(s)}{1+G(s)H(s)} \ $で与えられる伝達関数において，分母の$ \ 1+G(s)H(s)=0 \ $で与えられる式を特性方程式と言い，特性方程式の根において，
　①根の実数部がすべて負であれば，安定
　②根の実数部が一つでも正であれば，不安定
　③根の実数部が$ \ 0 \ $，すなわち純虚数であれば，安定限界（漸近安定）
となります。

【解答】

(1)解答：ニ
ワンポイント解説「2.特性方程式による安定判別」より，制御対象の特性方程式は，
\[
\begin{eqnarray}
s^{2}-4&=&0 \\[ 5pt ] \end{eqnarray}
\] で与えられ，その根は，
\[
\begin{eqnarray}
s^{2}&=&4 \\[ 5pt ] s&=&±2 \\[ 5pt ] \end{eqnarray}
\] となる。根に$ \ 2 \ $を含むので，制御対象は不安定となる。

(2)解答：ワ
ワンポイント解説「1.$ \ \mathrm {PID} \ $制御」の通り，$ \ \mathrm {PID} \ $補償器の式は，
\[
\begin{eqnarray}
G(s)&=&K_{\mathrm {p}}\left( 1+\frac {1}{T_{\mathrm {I}}s}+T_{\mathrm {D}}s\right) 　　・・・・・・・・・・・①　\\[ 5pt ] \end{eqnarray}
\] となるので，問題図の$ \ \mathrm {PID} \ $補償器の式を変形すると，
\[
\begin{eqnarray}
\frac {U(s)}{E(s)}&=&K_{1}+\frac {K_{2}}{s}+K_{3}s \\[ 5pt ] &=&K_{1}\left( 1+\frac {K_{2}}{K_{1}s}+\frac {K_{3}}{K_{1}}s\right)　・・・・・・・・・・・②　\\[ 5pt ] \end{eqnarray}
\] となる。したがって，①及び②を比較すると，積分時間$ \ T_{\mathrm {I}} \ $は，
\[
\begin{eqnarray}
T_{\mathrm {I}}&=&\frac {K_{1}}{K_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
(4)解答：ヲ
$ \ R(s) \ $から$ \ Y(s) \ $までの伝達関数は，
\[
\begin{eqnarray}
\frac {Y(s)}{R(s)}&=&\frac {\displaystyle \left( K_{1}+\frac {K_{2}}{s}+K_{3}s\right) \cdot \frac {10}{s^{2}-4}}{\displaystyle 1+\left( K_{1}+\frac {K_{2}}{s}+K_{3}s\right) \cdot \frac {10}{s^{2}-4}} \\[ 5pt ] &=&\frac {\displaystyle \left( K_{1}+\frac {K_{2}}{s}+K_{3}s\right) \cdot 10}{\displaystyle s^{2}-4+\left( K_{1}+\frac {K_{2}}{s}+K_{3}s\right) \cdot 10} \\[ 5pt ] &=&\frac {\displaystyle \left( K_{1}s+K_{2}+K_{3}s^{2}\right) \cdot 10}{\displaystyle s^{3}-4s+\left( K_{1}s+K_{2}+K_{3}s^{2}\right) \cdot 10} \\[ 5pt ] &=&\frac {10K_{3}s^{2}+10 K_{1}s+10K_{2}}{s^{3}+10K_{3}s^{2}+\left( 10K_{1}-4\right) s+10K_{2}}　・・・・・・・・・・・③　 \\[ 5pt ] \end{eqnarray}
\] となる。ここで，閉ループ伝達関数の望ましい極が，$ \ -30 \ $，$ \ -3±\mathrm {j}4 \ $になる，すなわち特性方程式の解が，$ \ -30 \ $，$ \ -3±\mathrm {j}4 \ $になるとあたえられているので，特性方程式は，
\[
\begin{eqnarray}
\left( s+30\right) \left( s+3+\mathrm {j}4\right) \left( s+3-\mathrm {j}4\right) &=&0 \\[ 5pt ] \left( s+30\right) \left[ \left( s+3\right) ^{2}+16\right] &=&0 \\[ 5pt ] \left( s+30\right) \left( s^{2}+6s+25\right) &=&0 \\[ 5pt ] s^{3}+36s^{2}+205s+750 &=&0 \\[ 5pt ] \end{eqnarray}
\] となる。この特性方程式が，③の特性方程式$ \ s^{3}+10K_{3}s^{2}+\left( 10K_{1}-4\right) s+10K_{2}=0 \ $と等しくなるためには，係数比較すると，
\[
\begin{eqnarray}
10K_{3} &=&36 \\[ 5pt ] 10K_{1}-4 &=&205 \\[ 5pt ] 10K_{2} &=&750 \\[ 5pt ] \end{eqnarray}
\] となる必要があるので，それぞれ解くと，
\[
\begin{eqnarray}
K_{3} &=&3.6 \\[ 5pt ] K_{1}&=&20.9 \\[ 5pt ] K_{2} &=&75 \\[ 5pt ] \end{eqnarray}
\] と求められる。