《機械》〈パワーエレクトロニクス〉[H28:問3] チョッパに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，チョッパに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

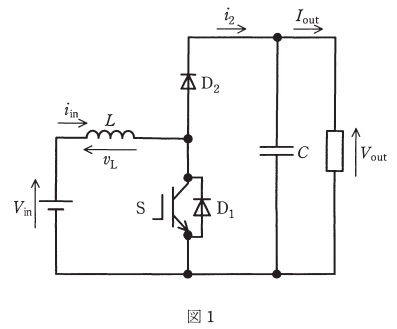
図1の$ \ \fbox {　（１）　} \ $チョッパの動作を考える。入力電圧は一定値$ \ V_{\mathrm{in}} \ \left[ \mathrm {V}\right] \ $とし，コンデンサの静電容量$ \ C \ \left[ \mathrm {F}\right] \ $は十分に大きく，出力の電圧及び電流を一定値$ \ V_{\mathrm{out}} \ \left[ \mathrm {V}\right] \ $及び$ \ I_{\mathrm{out}} \ \left[ \mathrm {A}\right] \ $と仮定する。バルブデバイス$ \ \mathrm {S} \ $及びダイオード$ \ \mathrm {D_{1}} \ $，$ \ \mathrm {D_{2}} \ $は理想スイッチ，理想ダイオードとする。バルブデバイス$ \ \mathrm {S} \ $は，周期的にオンとオフを繰り返し，$ \ 1 \ $周期中のオンしている時間を$ \ T_{\mathrm{on}} \ \left[ \mathrm {s}\right] \ $，オフしている時間を$ \ T_{\mathrm{off}} \ \left[ \mathrm {s}\right] \ $とすると，周期は$ \ T_{\mathrm{on}}+T_{\mathrm{off}} \ $となる。また，直流リアクトルのインダクタンスを$ \ L \ \left[ \mathrm {H}\right] \ $とし，入力電流は常に$ \ i_{\mathrm{in}} > 0 \ $とする。
ここで，$ \ \mathrm {S} \ $がオンしている$ \ T_{\mathrm{on}} \ $の期間中は，直流リアクトルには入力電圧$ \ V_{\mathrm{in}} \ $が印加して$ \ v_{L}=V_{\mathrm{in}} \ $となり，入力電流$ \ i_{\mathrm{in}} \ \left[ \mathrm {A}\right] \ $の単位時間当たりの変化は，$ \ \displaystyle \frac {\mathrm {d}i_{\mathrm{in}}}{\mathrm {d}t}=\frac {V_{\mathrm{in}}}{L} \ \left[ \mathrm {A/s}\right] \ $となる。一方，$ \ \mathrm {S} \ $がオフしている$ \ T_{\mathrm{off}} \ $の期間中は，$ \ \displaystyle \frac {\mathrm {d}i_{\mathrm{in}}}{\mathrm {d}t}= \ \fbox {　（２）　} \ $となる。
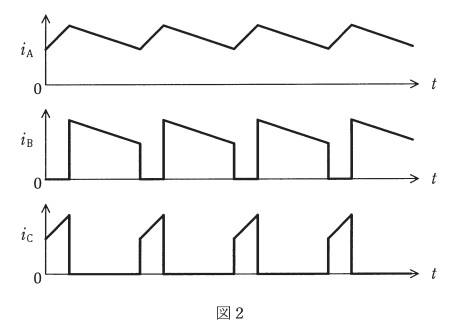
チョッパが動作してから十分に時間が経つと，入力電流$ \ i_{\mathrm{in}} \ $は周期的な繰り返し波形となる。入力電流$ \ i_{\mathrm{in}} \ $が周期的な繰り返し波形となるためには，$ \ \fbox {　（３）　} \ =0 \ $でなければならないので，出力電圧は，$ \ V_{\mathrm{out}}= \ \fbox {　（４）　} \ V_{\mathrm{in}} \ $となる。このとき，ダイオード$ \ \mathrm {D_{2}} \ $を通る電流$ \ i_{2} \ \left[ \mathrm {A}\right] \ $は図2の$ \ \fbox {　（５）　} \ $の波形となる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　i_{\mathrm {C}}　　　&（ロ）&　\frac {T_{\mathrm{on}}}{T_{\mathrm{off}}}　　　&（ハ）&　-\frac {V_{\mathrm{out}}}{L} \\[ 5pt ] &（ニ）&　V_{\mathrm{in}}T_{\mathrm{on}}+V_{\mathrm{out}}T_{\mathrm{off}}　　　&（ホ）&　-\frac {V_{\mathrm{in}}}{L}　　　&（ヘ）&　i_{\mathrm {B}} \\[ 5pt ] &（ト）&　降　圧　　　&（チ）&　\frac {T_{\mathrm{on}}+T_{\mathrm{off}}}{T_{\mathrm{off}}}　　　&（リ）&　\frac {T_{\mathrm{on}}}{T_{\mathrm{on}}+T_{\mathrm{off}}} \\[ 5pt ] &（ヌ）&　昇　圧　　　&（ル）&　V_{\mathrm{in}}T_{\mathrm{on}}+\left( V_{\mathrm{in}}-V_{\mathrm {out}}\right) T_{\mathrm{off}}　　　&（ヲ）&　\frac {V_{\mathrm{in}}-V_{\mathrm{out}}}{L} \\[ 5pt ] &（ワ）&　V_{\mathrm{in}}T_{\mathrm{on}}-V_{\mathrm{out}}T_{\mathrm{off}}　　　&（カ）&　i_{\mathrm {A}}　　　&（ヨ）&　昇降圧
\end{eqnarray}
\]

【ワンポイント解説】

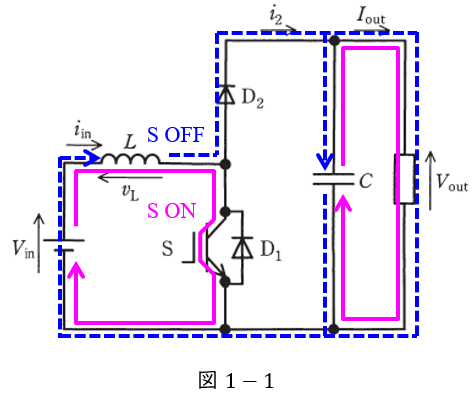
難易度は普通としましたが，慣れている人には易しい問題であるかもしれません。昇圧チョッパのメカニズムに関しては三種では結果を覚えるのみで対応できたかもしれませんが，二種以上ではその中身が問われます。本問で直流チョッパの考え方をきちんと理解しておきましょう。本問では図1-1のように，バルブデバイス$ \ \mathrm {S} \ $が$ \ \mathrm {ON} \ $の時赤線部に電流が流れ，バルブデバイス$ \ \mathrm {S} \ $が$ \ \mathrm {OFF} \ $の時青線部に電流が流れます。

【関連する「電気の神髄」記事】

　　2象限チョッパ回路（可逆チョッパ回路）

【解答】

(1)解答：ヌ
$ \ T_{\mathrm{off}} \ $の時，電源電圧に加えてリアクトル$ \ L \ $に蓄えられた電磁エネルギーが$ \ V_{\mathrm{out}} \ $にかかるので，この回路は昇圧チョッパとなる。

(2)解答：ヲ
$ \ \mathrm {S} \ $が$ \ \mathrm {OFF} \ $の時の回路方程式は，
\[
V_{\mathrm{in}}=L\frac {\mathrm {d}i_{\mathrm{in}}}{\mathrm {d}t}+V_{\mathrm{out}}
\] であるから，これを整理すると，
\[
\frac {\mathrm {d}i_{\mathrm{in}}}{\mathrm {d}t}=\frac {V_{\mathrm{in}}-V_{\mathrm{out}}}{L}
\] と求められる。

(3)解答：ル
題意より，$ \ i_{\mathrm{in}} \ $が繰り返し波形となるためには，$ \ \mathrm {S} \ $が$ \ \mathrm {ON} \ $の時と$ \ \mathrm {OFF} \ $の時の$ \ i_{\mathrm{in}} \ $の変化量が等しくなければならないので，
\[
\begin{eqnarray}
\frac {V_{\mathrm{in}}}{L}T_{\mathrm{on}}+\frac {V_{\mathrm{in}}-V_{\mathrm{out}}}{L}T_{\mathrm{off}}=0 \\[ 5pt ] V_{\mathrm{in}}T_{\mathrm{on}}+\left( V_{\mathrm{in}}-V_{\mathrm{out}}\right) T_{\mathrm{off}}=0
\end{eqnarray}
\] となる。

(4)解答：チ
(3)の解答の式を$ \ V_{\mathrm{out}} \ $について整理すると，
\[
V_{\mathrm{out}}=\frac {T_{\mathrm{on}}+T_{\mathrm{off}}}{T_{\mathrm{off}}}V_{\mathrm{in}}
\] となる。

(5)解答：ヘ
図1-1の通り，$ \ \mathrm {S} \ $が$ \ \mathrm {ON} \ $の時，$ \ D_{2} \ $には電流が流れないので，$ \ i_{2}=0 \ $となる。
また，$ \ \mathrm {S} \ $が$ \ \mathrm {OFF} \ $の時，$ \ D_{2} \ $には$ \ i_{\mathrm{in}} \ $と同じ大きさの電流が流れる。$ \ i_{\mathrm{in}} \ $は最初，リアクトルに蓄えられたエネルギーで大きな電流が流れるがその後リアクトルのエネルギーの減少とともに電流値も小さくなっていく。
よって，$ \ \mathrm {D_{2}} \ $を通る電流$ \ i_{2} \ \left[ \mathrm {A}\right] \ $は図2の$ \ i_{\mathrm {B}} \ $となる。