《機械》〈パワーエレクトロニクス〉[R01:問3]単相交流電力調整装置に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，単相交流電力調整装置に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

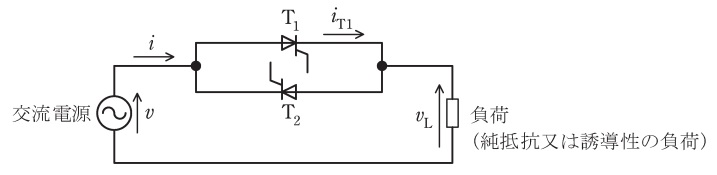
同じ制御遅れ角で点弧されるサイリスタが逆並列接続された単相交流電力調整装置を図に示す。まず負荷が純抵抗$ \ R \ $の場合の運転について考える。

電源電圧を$ \ v=\sqrt {2}V\sin \omega t \ $とすると，サイリスタ$ \ \mathrm {T}_{1} \ $，$ \ \mathrm {T}_{2} \ $に印加される可能性がある電圧の最大値は$ \ \fbox {　（１）　} \ $である。制御遅れ角$ \ \alpha \ $で運転したとき，二つあるサイリスタのうち一方のサイリスタ$ \ \mathrm {T}_{1} \ $に流れる電流$ \ i_{\mathrm {T1}} \ $の平均値$ \ I_{\mathrm {0\left( av\right) }} \ $を求めるためには，$ \ \omega t \ $が$ \ \alpha \ $から$ \ \pi \ $までの負荷電圧波形から$ \ 1 \ $サイクル$ \ ( 0 \ $から$ \ 2\pi ) \ $の平均値を計算して$ \ R \ $で除すればよい。したがって，$ \ I_{\mathrm {0\left( av\right) }}=\fbox {　（２）　} \ \times \left( 1+\cos \alpha \right) \ $となる。使用するサイリスタはこれらの電圧，電流値を参考にして選択される。

負荷で消費される交流電力は，制御遅れ角$ \ \alpha \ $によって調整する。$ \ \alpha \ $が$ \ \displaystyle \frac {\pi }{2} \ $のときに負荷で消費される電力は，$ \ \alpha \ $が$ \ 0 \ $のときに消費される電力に対して$ \ \fbox {　（３）　} \ $となる。

次に，負荷が力率角$ \ \theta \ $の誘導性負荷の場合の運転について考える。

この交流電力調整装置で出力の交流電圧すなわち交流電力を調整することができるのは，制御遅れ角$ \ \alpha \ $を$ \ \fbox {　（４）　} \ $の範囲で運転したときである。負荷が純インダクタンスであったときに，出力の交流電圧を調整できるある制御遅れ角$ \ \alpha _{1} \ $で運転したとすると，入力の交流電流$ \ i \ $は，$ \ v \ $に対して基本波ベースで位相が$ \ \fbox {　（５）　} \ $となり，無効電力の大きさを調整する手段に使われる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　同相　　　　　&（ロ）&　90° \ 進み　　　　　&（ハ）&　順方向に \ \sqrt {2}V \ ，逆方向に \ \sqrt {2}V \\[ 5pt ] &（ニ）&　\frac {1}{\sqrt {2}} 　　　　　&（ホ）&　0 \ ＜ \ \alpha \ ＜ \ \theta　　　　　&（ヘ）&　\frac {\sqrt {2}V}{\pi R} \\[ 5pt ] &（ト）&　\theta \ ＜ \ \alpha \ ＜ \ \pi　　　　　&（チ）&　\frac {1}{4}　　　　　&（リ）&　順方向に \ 0 \ ，逆方向に \ \sqrt {2}V \\[ 5pt ] &（ヌ）&　90° \ 遅れ　　　　　&（ル）&　\frac {V}{\sqrt {2} R}　　　　　&（ヲ）&　\frac {V}{\sqrt {2}\pi R} \\[ 5pt ] &（ワ）&　\frac {\pi }{2} \ ＜ \ \alpha \ ＜ \ \theta　　　　　　　&（カ）&　\frac {1}{2}　　　　　&（ヨ）&　順方向に \ \sqrt {2}V \ ，逆方向に \ 0 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

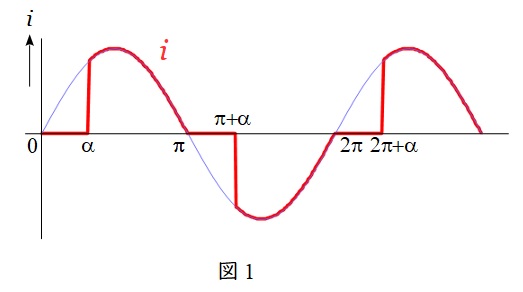
パワーエレクトロニクスは電流がどのようになるかを把握することが最も正解に近くなる方法となります。本問では制御遅れ角$ \ \alpha \ $において，電源電流が図1のようになることを理解していることが前提となります。パワーエレクトロニクスを苦手としている受験生は多いので，正答率はあまり高くないかもしれませんが，パワーエレクトロニクスの問題としては易しめの問題となります。

1.サイリスタ
アノード―カソード間に順電圧をかけた状態で，ゲートにパルス電流を流すとターンオンする素子です。
一旦順方向に電流が流れるとゲート信号がなくなってもオン状態を維持します。
順方向の電流を保持電流以下にする，もしくは逆方向に電圧をかけるとサイリスタをオフにすることができます。

2.平均値と実効値の定義
$ \ f( \theta ) \ $を周期$ \ 2 \pi \ $の周期関数であるとしたとき，平均値と実効値は以下の通りとなります。
①平均値$ \ F_{\mathrm {av}} \ $
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{2\pi }\int _{0}^{2\pi }f( \theta ) \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] ②実効値$ \ F \ $　
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{2\pi} \int _{0}^{2\pi} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ハ
電源電圧が$ \ v=\sqrt {2}V\sin \omega t \ $となるので，サイリスタに印加される可能性がある電圧値は制御遅れ角が$ \ \displaystyle \frac {\pi }{2} \ ＜ \ \alpha \ ＜ \ \pi \ $である時，順方向には電圧位相が$ \ \displaystyle \omega t =\frac {\pi }{2} \ $になるとサイリスタに印加される電圧が$ \ \sqrt {2}V \ $，逆方向には電圧位相が$ \ \displaystyle \omega t =\frac {3\pi }{2} \ $になるとサイリスタに印加される電圧が$ \ \sqrt {2}V \ $となります。

(2)解答：ヲ
題意より，制御遅れ角$ \ \alpha \ $で運転したときの平均値$ \ I_{\mathrm {0\left( av\right) }} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {0\left( av\right) }}&=&\frac {1}{R}\times \frac {1}{2\pi }\int _{\alpha }^{\pi } \sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=&\frac {V}{\sqrt {2}\pi R}\int _{\alpha }^{\pi } \sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=&\frac {V}{\sqrt {2}\pi R}\left[ -\cos \omega t\right] _{\alpha }^{\pi } \\[ 5pt ] &=&\frac {V}{\sqrt {2}\pi R}\left( 1+\cos \alpha \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：カ
制御遅れ角$ \ \alpha \ $が$ \ 0 \ $のとき，$ \ \omega t =0 \ $から$ \ \displaystyle \omega t =\frac {\pi }{2} \ $及び$ \ \displaystyle \omega t =\frac {\pi }{2} \ $から$ \ \omega t =\pi \ $までに消費される電力は等しい。したがって，$ \ \alpha \ $が$ \ \displaystyle \frac {\pi }{2} \ $のときに負荷で消費される電力は，$ \ \alpha \ $が$ \ 0 \ $のときに消費される電力に対して$ \ \displaystyle \frac {1}{2} \ $となる。

(4)解答：ト
任意の電流に対して，負荷が力率角$ \ \theta \ $の誘導性負荷の電流は，$ \ i=\sqrt {2}I\sin \left( \omega t-\theta \right) \ $と表すことができるので，交流電力を調整できるのは電圧電流が正となる位相すなわち$ \ \theta \ ＜ \ \alpha \ ＜ \ \pi \ $となる。

(5)解答：ヌ
負荷が純インダクタンスであるので，交流電流$ \ i \ $は，$ \ v \ $に対して基本波ベースで位相が$ \ 90° \ $遅れとなります。