《機械》〈回転機〉[R02:問3]誘導電動機の速度制御に関する計算・空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘導電動機の速度制御に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

誘導電動機の速度を自由に，かつ広範囲に制御できれば，回転機の可変速制御を必要とする分野で広く応用できる。ここに誘導電動機の同期角速度を$ \ \omega _{\mathrm {s}} \ $，極数を$ \ 2p \ $，滑りを$ \ s \ $，電源周波数を$ \ f \ $とすると，回転角速度$ \ \omega _{\mathrm {m}} \ $は，次式のように表現される。
\[
\begin{eqnarray}
\omega _{\mathrm {m}}&=&\omega _{\mathrm {s}}\left( 1-s \right) = \ \fbox {　（１）　} \ \left( 1-s \right) 　・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] $ \ ① \ $式より，極数，滑りあるいは周波数のいずれかを変化できれば，誘導電動機の速度は制御できることになる。

極数を変化させる方法はあらかじめ極数が変更できるように巻線の接続法を工夫しておき，必要に応じてスイッチを切り換えることにより変える方法であるが，段階的な制御であり連続した可変速を必要とする用途には不向きである。

滑りを変化させる方式では，誘導電動機の発生トルクが入力電圧の$ \ \fbox {　（２）　} \ $ことを利用する$ \ \fbox {　（３）　} \ $法がある。

本方式は滑りの増加とともに電動機の効率が悪化するので，電動機の効率を重視する用途には不向きである。

周波数を連続的に制御する方式は，近年の自励式インバータ電源（電力変換器）による駆動が可能となったことにより広く採用されるようになった。例えばオープンループ制御のインバータ電源による駆動では$ \ \fbox {　（４）　} \ $が行われ，電動機の$ \ \fbox {　（５）　} \ $が飽和しないようにしている。さらに精密な回転機の制御が求められる時には，ベクトル制御による高精度制御が行われる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　二次電力制御　　　　　&（ロ）&　V／f \ 一定制御　　　　　&（ハ）&　2 \ 乗に比例する \\[ 5pt ] &（ニ）&　抵抗制御　　　　　&（ホ）&　定電力制御　　　　　&（ヘ）&　\frac {\pi f}{2p} \\[ 5pt ] &（ト）&　磁束　　　　　&（チ）&　比例推移制御　　　　　&（リ）&　2 \ 乗に反比例する \\[ 5pt ] &（ヌ）&　\frac {p}{2\pi f}　　　　　&（ル）&　一次電圧制御　　　　　&（ヲ）&　銅損 \\[ 5pt ] &（ワ）&　\frac {2\pi f}{p}　　　　　&（カ）&　同期速度　　　　　&（ヨ）&　大きさに関係なく一定である \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘導電動機の速度制御に関する問題です。
基本的な等価回路，トルクの知識を有しているかを問う問題となっています。等価回路からトルクを導出する計算過程等は二次試験でも必須の知識となるので，確実に理解しておきましょう。

1.三相誘導電動機の同期速度$ \ N_{\mathrm {s}} \ $
三相誘導電動機の極数が$ \ p \ $，電源の周波数が$ \ f \ \mathrm {[Hz]} \ $の時，同期速度$ \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ $は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

2.三相誘導電動機の回転数$ \ N \ $と角速度$ \ \omega \ $の関係
三相誘導電動機の回転数$ \ N \ \mathrm {[{min}^{-1}]} \ $とすると，角速度$ \ \omega \ \mathrm {[rad/s]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {2\pi N}{60} \\[ 5pt ] \end{eqnarray}
\] となります。したがって，同期角速度$ \ \omega _{\mathrm {s}} \ \mathrm {[rad/s]} \ $は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}}&=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] で求めることができます。

3.誘導機の滑り$ \ s \ $
誘導機の同期速度が$ \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ $，回転数が$ \ N \ \mathrm {[{min}^{-1}]} \ $である時，誘導機の滑り$ \ s \ $は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となり，上式を変形すると，
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ] N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ] &=&N_{\mathrm {s}}\left( 1-s\right) \\[ 5pt ] \end{eqnarray}
\] となります。さらに上式を変形すると，$ \ \omega \ \mathrm {[rad/s]} \ $及び同期角速度$ \ \omega _{\mathrm {s}} \ \mathrm {[rad/s]} \ $においても，
\[
\begin{eqnarray}
N&=&N_{\mathrm {s}}\left( 1-s\right) \\[ 5pt ] \frac {2\pi N}{60}&=&\frac {2\pi N_{\mathrm {s}}}{60}\left( 1-s\right) \\[ 5pt ] \omega &=&\omega _{\mathrm {s}}\left( 1-s\right) \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。

4.二次入力$ \ P_{2} \ $と出力$ \ P_{\mathrm {o}} \ $と二次銅損$ \ P_{\mathrm {c2}} \ $の関係
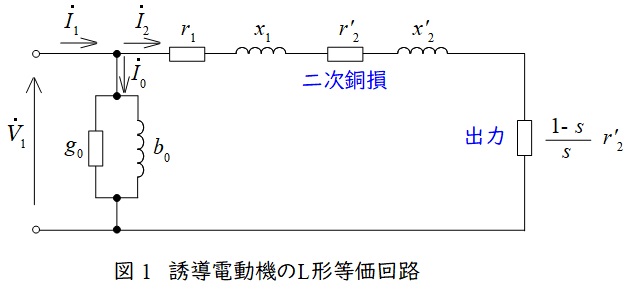
誘導電動機の$ \ \mathrm {L} \ $形等価回路は図1のようになります。図1において，$ \ {\dot V}_{1} \ $は一次側端子電圧，$ \ {\dot I}_{1} \ $は一次電流，$ \ {\dot I}_{2} \ $は二次電流，$ \ {\dot I}_{0} \ $は励磁電流，$ \ r_{1} \ $は一次巻線抵抗，$ \ r_{2}^{\prime } \ $は二次巻線抵抗の一次換算，$ \ x_{1} \ $は一次漏れリアクタンス，$ \ x_{2}^{\prime } \ $は二次漏れリアクタンスの一次換算，$ \ s \ $は滑りとなります。
図1より，出力$ \ P_{\mathrm {o}} \ $，二次銅損$ \ P_{\mathrm {c2}} \ $，二次入力$ \ P_{2} \ $は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& \frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力$ \ P_{2} \ $，出力$ \ P_{\mathrm {o}} \ $，二次銅損$ \ P_{\mathrm {c2}} \ $には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

5.出力$ \ P_{\mathrm {o}} \ $とトルク$ \ T \ $の関係
誘導電動機の出力$ \ P_{\mathrm {o}} \ \mathrm {[W]} \ $とトルク$ \ T \ \mathrm {[N/m]} \ $には，角速度を$ \ \omega \ \mathrm {[rad/s]} \ $とすると，
\[
\begin{eqnarray}
T &=& \frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ワ
ワンポイント解説「1.三相誘導電動機の同期速度$ \ N_{\mathrm {s}} \ $」及び「2.三相誘導電動機の回転数$ \ N \ $と角速度$ \ \omega \ $の関係」の通り，回転角速度$ \ \omega _{\mathrm {m}} \ $は，極数が$ \ 2p \ $であることに注意すると，
\[
\begin{eqnarray}
\omega _{\mathrm {m}}&=&\omega _{\mathrm {s}}\left( 1-s \right) \\[ 5pt ] &=&\frac {4\pi f}{2p}\left( 1-s \right) \\[ 5pt ] &=&\frac {2\pi f}{p}\left( 1-s \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ハ
ワンポイント解説「4.二次入力$ \ P_{2} \ $と出力$ \ P_{\mathrm {o}} \ $と二次銅損$ \ P_{\mathrm {c2}} \ $の関係」の図1より，二次電流$ \ I_{2} \ $は，
\[
\begin{eqnarray}
I_{2}&=&\frac {V_{1}}{\displaystyle \sqrt {\left( r_{1} +\frac {{r_{2}}^{\prime }}{s}\right) ^{2}+\left( x_{1} +{x_{2}}^{\prime }\right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] であり，出力$ \ P_{\mathrm {o}} \ $は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& \frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] &=& \frac {1-s}{s}r_{2}^{\prime }\left\{ \frac {V_{1}}{\displaystyle \sqrt {\left( r_{1} +\frac {{r_{2}}^{\prime }}{s}\right) ^{2}+\left( x_{1} +{x_{2}}^{\prime }\right) ^{2}}}\right\} ^{2} \\[ 5pt ] &=& \frac {1-s}{s}\frac {r_{2}^{\prime }{V_{1}}^{2}}{\displaystyle \left( r_{1} +\frac {{r_{2}}^{\prime }}{s}\right) ^{2}+\left( x_{1} +{x_{2}}^{\prime }\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「5.出力$ \ P_{\mathrm {o}} \ $とトルク$ \ T \ $の関係」の通り，トルク$ \ T \ $は，
\[
\begin{eqnarray}
T &=& \frac {P_{\mathrm {o}}}{\omega _{\mathrm {m}}} \\[ 5pt ] &=& \frac {\displaystyle \frac {1-s}{s}\frac {r_{2}^{\prime }{V_{1}}^{2}}{\displaystyle \left( r_{1} +\frac {{r_{2}}^{\prime }}{s}\right) ^{2}+\left( x_{1} +{x_{2}}^{\prime }\right) ^{2}}}{\displaystyle \frac {2\pi f}{p}\left( 1-s \right) } \\[ 5pt ] &=& \frac {p}{2\pi fs}\frac {r_{2}^{\prime }{V_{1}}^{2}}{\displaystyle \left( r_{1} +\frac {{r_{2}}^{\prime }}{s}\right) ^{2}+\left( x_{1} +{x_{2}}^{\prime }\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められるので，発生トルクは入力電圧の$ \ 2 \ $乗に比例することがわかる。

※　試験本番では，ここまで導出せずに，等価回路から出力が入力電圧の$ \ 2 \ $乗に比例し，そこからトルクも$ \ 2 \ $乗に比例すると類推できると良いです。

(3)解答：ル
題意より解答候補は，（イ）二次電力制御，（ロ）$ V／f \ $一定制御，（ニ）抵抗制御，（ホ）定電力制御，（チ）比例推移制御，（ル）一次電圧制御，等になると思います。
入力電圧は一次電圧なので，誘導電動機のトルクを入力電圧で制御する方法を，一次電圧制御法といいます。

(4)解答：ロ
題意より解答候補は，（イ）二次電力制御，（ロ）$ V／f \ $一定制御，（ニ）抵抗制御，（ホ）定電力制御，（チ）比例推移制御，（ル）一次電圧制御，等になると思います。
磁束$ \ \mathit {\Phi } \ $は励磁電流$ \ I_{0} \ $に比例し，励磁電流$ \ I_{0} \ $は$ \ g_{0} \ $が小さいとすると$ \ b_{0} \ $にほぼ比例します。
$ \ \displaystyle b_{0}=\frac {1}{2\pi fL} \ $であり，$ \ b_{0} \ $は周波数$ \ f \ $に反比例するので，磁束$ \ \mathit {\Phi } \ $は周波数$ \ f \ $にほぼ反比例することがわかります。
また，図1の等価回路において，オームの法則より励磁電流$ \ I_{0} \ $は$ \ V_{1} $に比例するので，磁束$ \ \mathit {\Phi } \ $は$ \ \displaystyle \frac {V}{f} \ $にほぼ比例することが分かります。
したがって，電動機の磁束が飽和しないように，インバータ電源による駆動では$ \ \displaystyle \frac {V}{f} \ $一定制御が行われます。

(5)解答：ト
題意より解答候補は，（ト）磁束，（ヲ）銅損，（カ）同期速度，等になると思います。
(4)の解答の通り，$ \ \displaystyle \frac {V}{f} \ $一定制御は磁束が飽和しないようにする制御です。