《機械》〈変圧器〉[R07:問3]単相変圧器の短絡試験に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，単相変圧器の試験に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

単相変圧器の短絡試験では，変圧器の二次側を短絡し，一次側に定格周波数の電圧を加えて，一次電圧$ \ \mathrm {[V]} \ $，一次電流$ \ \mathrm {[A]} \ $，及び消費電力$ \ \mathrm {[W]} \ $を測定する。この時の一次電圧は，定格電圧よりも十分に低く，励磁電流による電圧降下を無視することができ，$ \ \fbox {　（１）　} \ $に等しい。この短絡試験の結果から，一次巻線抵抗$ \ r_{1} \ $と二次巻線抵抗$ \ r_{2} \ $の一次換算値の和$ \ r \ $と，一次漏れリアクタンスと二次漏れリアクタンスの一次換算値の和$ \ x \ $を求めることができる。抵抗$ \ r \ $は変圧器の巻数比$ \ a \ $（一次側の巻数を二次側の巻数で除したもの）を用いると$ \ \fbox {　（２）　} \ $として表すことができる。この試験で得られる抵抗$ \ r \ $は直流を用いて測定した一次側及び二次側の巻線抵抗から求めた値に比べて大きくなる。その要因の一つとして，電流密度が$ \ \fbox {　（３）　} \ $で高まる表皮効果があげられる。

変圧器の短絡試験により，一次電圧$ \ 230 \ \mathrm {V} \ $，一次電流$ \ 25 \ \mathrm {A} \ $，及び消費電力$ \ 1 \ 875 \ \mathrm {W} \ $が得られたとき，$ \ r= \ \fbox {　（４）　} \ \mathrm {\Omega } \ $，$ \ x= \ \fbox {　（５）　} \ \mathrm {\Omega } \ $となる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　2.49　　　　&（ロ）&　3.00　　　　　&（ハ）&　75.6 \\[ 5pt ] &（ニ）&　8.70　　　　　&（ホ）&　9.20　　　　　&（ヘ）&　9.68 \\[ 5pt ] &（ト）&　導体の端部　　　　　&（チ）&　導体の中心　　　　　&（リ）&　インピーダンス電圧 \\[ 5pt ] &（ヌ）&　短絡電圧　　　　　&（ル）&　開放電圧　　　　　&（ヲ）&　導体の表面 \\[ 5pt ] &（ワ）&　r_{1}+ar_{2}　　　　　&（カ）&　r_{1}+a^{2}r_{2}　　　　　&（ヨ）&　r_{1}+\frac {1}{a^{2}}r_{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

単相変圧器の短絡試験に関する問題です。
電験では無負荷試験と合わせ二次試験においても出題される可能性がある内容です。
どのような試験か，説明できるレベルまで引き上げておくようにしましょう。

1.変圧器の$ \ \mathrm {L} \ $形等価回路（一次換算）
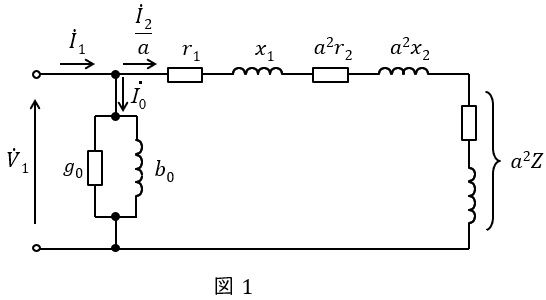
変圧器の一次換算等価回路を図1に示します。ただし，$ \ {\dot V}_{1} \ \mathrm {[V]} \ $は一次側端子電圧，$ \ {\dot I}_{1} \ \mathrm {[A]} \ $は一次電流，$ \ {\dot I}_{2} \ \mathrm {[A]} \ $は二次電流，$ \ {\dot I}_{0} \ \mathrm {[A]} \ $は励磁電流，$ \ r_{1} \ \mathrm {[\Omega ]} \ $は一次巻線抵抗，$ \ r_{2} \ \mathrm {[\Omega ]} \ $は二次巻線抵抗，$ \ x_{1} \ \mathrm {[\Omega ]} \ $は一次漏れリアクタンス，$ \ x_{2} \ \mathrm {[\Omega ]} \ $は二次漏れリアクタンス，$ \ a \ $は変圧比（巻数比）となります。

2.無負荷試験の等価回路
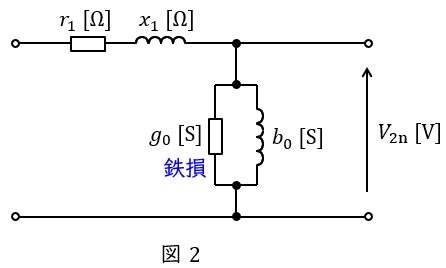
変圧器の無負荷試験は一次側を開放して，二次側に定格電圧を加える試験です。測定される電力は鉄損となり，測定される電力と電流から，励磁コンダクタンス$ \ g_{0} \ \mathrm {[S]} \ $及び励磁サセプタンス$ \ b_{0} \ \mathrm {[S]} \ $を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが，二次側開放で一次側に定格電圧を加えても同様に求められます。

3.短絡試験の等価回路
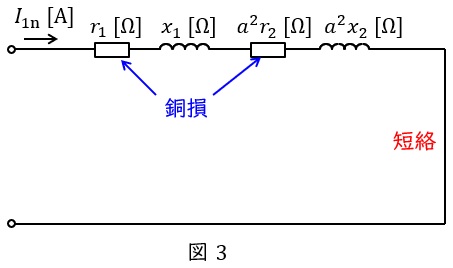
変圧器の短絡試験は二次側を短絡して，一次側にインピーダンス電圧を加えて，定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると，測定される電力は銅損となります。測定される電力と電流から，高圧側換算の巻線抵抗$ \ R=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ $及び漏れリアクタンス$ \ X=x_{1}+a^{2}x_{2} \ \mathrm {[\Omega ]} \ $を求めることが可能となります。

4.表皮効果
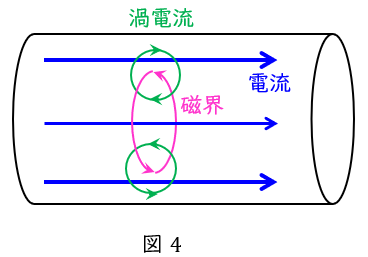
交流電流において，導体内を流れる電流によりアンペールの法則に沿った磁界が発生し，その発生した磁界の変化によりファラデーの電磁誘導の法則に沿った渦電流が発生することで，導体内の電流分布が外側に集中する現象です。
電線の断面積が大きい電線では無視できなくなり，角周波数と透磁率，導電率が大きくなるほど顕著となります。

【解答】

(1)解答：リ
題意より解答候補は，（リ）インピーダンス電圧，（ヌ）短絡電圧，（ル）開放電圧，になると思います。
ワンポイント解説「3.短絡試験の等価回路」の通り，短絡試験時の一次電圧は，インピーダンス電圧に等しいです。

(2)解答：カ
題意より解答候補は，（ワ）$ \ r_{1}+ar_{2} \ $，（カ）$ \ r_{1}+a^{2}r_{2} \ $，（ヨ）$ \ r_{1}+\frac {1}{a^{2}}r_{2} \ $，になると思います。
ワンポイント解説「3.短絡試験の等価回路」の通り，抵抗$ \ r \ $は変圧器の巻数比$ \ a \ $を用いて$ \ r_{1}+a^{2}r_{2} \ $として表すことができます。

(3)解答：ヲ
題意より解答候補は，（ト）導体の端部，（チ）導体の中心，（ヲ）導体の表面，になると思います。
ワンポイント解説「4.表皮効果」の通り，表皮効果は電流密度が導体の表面で高まる現象です。

(4)解答：ロ
一次電流$ \ I_{1}= 25 \ \mathrm {[A]} \ $，消費電力$ \ P=1 \ 875 \ \mathrm {[W]} \ $なので，一次二次巻線抵抗の一次換算$ \ r \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
P&=&r{I_{1}}^{2} \\[ 5pt ] r&=&\frac {P}{{I_{1}}^{2}} \\[ 5pt ] &=&\frac {1 \ 875}{25^{2}} \\[ 5pt ] &=&3 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
一次電圧$ \ V_{1}= 230 \ \mathrm {[V]} \ $，一次電流$ \ I_{1}= 25 \ \mathrm {[A]} \ $より，変圧器の一次換算のインピーダンス$ \ Z \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
Z&=&\frac {V_{1}}{I_{1}} \\[ 5pt ] &=&\frac {230}{25} \\[ 5pt ] &=&9.2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，一次二次漏れリアクタンスの一次換算$ \ x \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
x&=&\sqrt {Z^{2}-r^{2}} \\[ 5pt ] &=&\sqrt {9.2^{2}-3^{2}} \\[ 5pt ] &≒&8.70 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。