【問題】
【難易度】★★★★☆(やや難しい)
変圧器の特性に関して,次の問に答えよ。
(1) 定格容量\( \ S_{\mathrm {n}}=100 \ \mathrm {kV\cdot A} \ \),定格一次電圧\( \ V_{\mathrm {1n}}=6600 \ \mathrm {V} \ \),定格二次電圧\( \ V_{\mathrm {2n}}=210 \ \mathrm {V} \ \),定格周波数\( \ 60 \ \mathrm {Hz} \ \)の単相変圧器がある。巻数比\( \ a \ \),定格一次電流\( \ I_{\mathrm {1n}} \ \mathrm {[A]} \ \)を求めよ。
(2) この変圧器の二次巻線端子を短絡し,一次巻線端子に定格周波数の電圧\( \ V_{\mathrm {1s}}=218 \ \mathrm {V} \ \)を印加したところ,二次側電流が定格電流となり,入力電力は,\( \ P_{\mathrm {1s}}=1200 \ \mathrm {W} \ \)であった。短絡インピーダンスの大きさ\( \ [%] \ \)を求めよ。
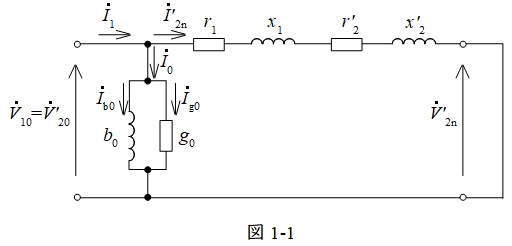
(3) 図1は二次側の諸量を一次側に換算した変圧器の簡易等価回路である。上記(2)の条件から,図中の巻線の抵抗\( \ r=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ \)及び漏れリアクタンス\( \ x=x_{1}+a^{2}x_{2} \ \mathrm {[\Omega ]} \ \)を求めよ。ただし,励磁アドミタンスは無視する。
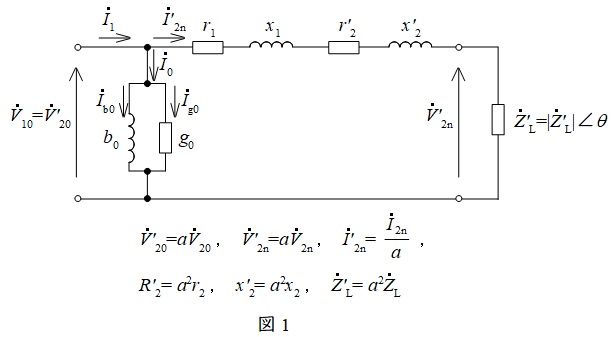
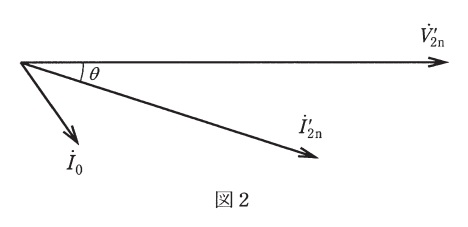
(4) 図1に示すように,二次巻線端子に力率\( \ \cos \theta \ \)の負荷\( \ \left( {\dot Z}_{\mathrm {L}}=\left| {\dot Z}_{\mathrm {L}}\right| ∠\theta \right) \ \)を接続して一次巻線電圧を\( \ V_{10} \ \)としたとき,負荷に定格電圧\( \ V_{\mathrm {2n}} \ \)が印加され定格電流\( \ I_{\mathrm {2n}} \ \)が流れた。図2は,このときの電圧電流ベクトル概略図の一部である。図2が答案用紙に印刷されているので,電圧\( \ {\dot V}^{\prime }_{20}\left( ={\dot V}_{10} \right) \ \)及び電流\( \ {\dot I}_{1} \ \),\( \ {\dot I}_{\mathrm {g0}} \ \),\( \ {\dot I}_{\mathrm {b0}} \ \)のベクトルを書き足して,ベクトル図を完成させよ。巻線抵抗\( \ r \ \)及び漏れリアクタンス\( \ x \ \)による電圧降下の成分も図中に明示せよ。
(5) 一次端子電圧を\( \ V_{\mathrm {10}} \ \)のままにして,無負荷としたときの二次端子電圧を\( \ V_{\mathrm {20}} \ \)とする。このとき,この変圧器の電圧の変動率\( \ \varepsilon \ \)を,次式で表す。
\[
\varepsilon =\frac {V_{\mathrm {20}}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 [%]
\]
これは,次式で近似できることを示せ。
\[
\varepsilon ≒\left( q_{\mathrm {R}}\cos \theta +q_{\mathrm {X}}\sin \theta \right) \times 100 [%]
\]
ただし,\( \ \displaystyle R=\frac {r}{a^{2}} \ \),\( \ \displaystyle X=\frac {x}{a^{2}} \ \),\( \ \displaystyle q_{\mathrm {R}}=\frac {RI_{\mathrm {2n}}}{V_{\mathrm {2n}}}≪1 \ \),\( \ \displaystyle q_{\mathrm {X}}=\frac {XI_{\mathrm {2n}}}{V_{\mathrm {2n}}}≪1 \ \)とする。また,必要に応じて,展開式\( \ \displaystyle \sqrt {1+\delta }=1+\frac {1}{2}\delta -\frac {1}{8}\delta ^{2}+・・・,( \left| \delta \right| < 1) \ \)を用いよ。
【ワンポイント解説】
百分率インピーダンスを使いこなせること,複雑な計算があること等かなりの能力が求められ,一種に出題されてもよいレベルの問題であると思います。この年の機械制御は問題毎の難易度格差が大きく,本問を選択した方は苦戦したのではないかと思います。
1.百分率インピーダンスの定義
単相変圧器の定格容量\( \ P_{\mathrm {n}} \ \),定格電圧\( \ V_{\mathrm {n}} \ \),定格電流\( \ I_{\mathrm {n}} \ \)とした時,インピーダンス\( \ Z \ \)のパーセントインピーダンス\( \ %Z \ \)は,
\[
\begin{eqnarray}
%Z&=& \frac {ZI_{\mathrm {n}}}{V_{\mathrm {n}}} \times 100 \\[ 5pt ]
&=& \frac {ZP_{\mathrm {n}}}{V^{2}_{\mathrm {n}}} \times 100 \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)巻数比\( \ a \ \),定格一次電流\( \ I_{\mathrm {1n}} \ \mathrm {[A]} \ \)
巻数比\( \ a \ \)は,一次電圧と二次電圧の比と等しいので,
\[
\begin{eqnarray}
a&=& \frac {V_{\mathrm {1n}}}{V_{\mathrm {2n}}} \\[ 5pt ]
&=& \frac {6600}{210} \\[ 5pt ]
&≒&31.429 → 31.4
\end{eqnarray}
\]
と求められる。また一次定格電流\( \ I_{\mathrm {1n}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {1n}}&=& \frac {S_{\mathrm {n}}}{V_{\mathrm {1n}}} \\[ 5pt ]
&=& \frac {100\times 10^{3}}{6600} \\[ 5pt ]
&≒&15.152 → 15.2 \ \mathrm {[A]}
\end{eqnarray}
\]
と求められる。
(2)短絡インピーダンスの大きさ\( \ [%] \ \)
短絡インピーダンスの大きさ\( \ Z_{\mathrm {s}} \ \)は題意より,
\[
Z_{\mathrm {s}}=\frac {V_{\mathrm {s}}}{I_{\mathrm {1n}}}
\]
であるから,ワンポイント解説「1.百分率インピーダンスの定義」より,短絡インピーダンスの大きさ\( \ %Z_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
%Z_{\mathrm {s}}&=& \frac {Z_{\mathrm {s}}I_{\mathrm {1n}}}{V_{\mathrm {1n}}} \times 100 \\[ 5pt ]
&=&\frac {\frac {V_{\mathrm {1s}}}{I_{\mathrm {1n}}}I_{\mathrm {1n}}}{V_{\mathrm {1n}}} \times 100 \\[ 5pt ]
&=&\frac {V_{\mathrm {1s}}}{V_{\mathrm {1n}}} \times 100 \\[ 5pt ]
&=&\frac {218}{6600} \times 100 \\[ 5pt ]
&≒&3.3030 → 3.30 \ \mathrm {[%]}
\end{eqnarray}
\]
と求められる。
(3)巻線の抵抗\( \ r=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ \)及び漏れリアクタンス\( \ x=x_{1}+a^{2}x_{2} \ \mathrm {[\Omega ]} \ \)
(2)の条件における等価回路は図1-1のようになる。無負荷試験時の結果より,
\[
\begin{eqnarray}
P_{\mathrm {1s}}&=& r I^{2}_{\mathrm {1n}} \\[ 5pt ]
r&=&\frac {P_{\mathrm {1s}}}{I^{2}_{\mathrm {1n}}}\\[ 5pt ]
&=&\frac {1200}{15.152^{2}} \\[ 5pt ]
&≒&5.2269 → 5.23 \ \mathrm {[\Omega]}
\end{eqnarray}
\]
となる。また,短絡インピーダンスの大きさ\( \ Z_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
Z_{\mathrm {s}}&=& \frac {218}{15.152} \\[ 5pt ]
&≒&14.388 \ \mathrm {[\Omega]}
\end{eqnarray}
\]
となるので,漏れリアクタンスの大きさは,
\[
\begin{eqnarray}
x&=&\sqrt {Z_{\mathrm {s}}^{2}-r^{2}} \\[ 5pt ]
&=&\sqrt {14.388^{2}-5.23^{2}} \\[ 5pt ]
&≒&13.404 → 13.4 \ \mathrm {[\Omega]}
\end{eqnarray}
\]
と求められる。
(4)電圧\( \ {\dot V}^{\prime }_{20}\left( ={\dot V}_{10} \right) \ \)及び電流\( \ {\dot I}_{1} \ \),\( \ {\dot I}_{\mathrm {g0}} \ \),\( \ {\dot I}_{\mathrm {b0}} \ \)のベクトルを書き足す
図2-2の通りとなる。
【作成手順】
① \( \ {\dot I}^{\prime }_{\mathrm {2n}} \ \)に平行に\( \ r{\dot I}^{\prime }_{\mathrm {2n}} \ \)を描く。
② \( \ {\dot I}^{\prime }_{\mathrm {2n}} \ \)に垂直に\( \ x{\dot I}^{\prime }_{\mathrm {2n}} \ \)を描く。
③ \( \ {\dot V}^{\prime }_{\mathrm {20}}={\dot V}^{\prime }_{\mathrm {2n}}+r{\dot I}^{\prime }_{\mathrm {2n}}+x{\dot I}^{\prime }_{\mathrm {2n}} \ \)となるように\( \ {\dot V}^{\prime }_{\mathrm {20}} \ \)を描く。
④ \( \ {\dot V}^{\prime }_{\mathrm {20}} \ \)と平行に\( \ {\dot I}_{\mathrm {g0}} \ \),垂直に\( \ {\dot I}_{\mathrm {b0}} \ \)を,\( \ {\dot I}_{\mathrm {g0}}+{\dot I}_{\mathrm {b0}}={\dot I}_{\mathrm {0}} \ \)となるように描く。
⑤ \( \ {\dot I}_{0}+{\dot I}^{\prime }_{\mathrm {2n}}={\dot I}_{\mathrm {1}} \ \)となるように描く。
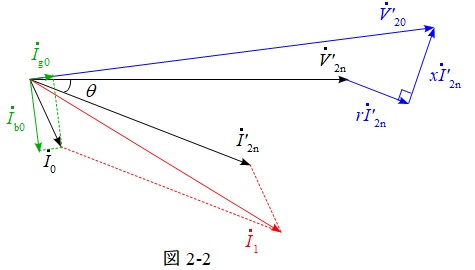
(5)近似式の証明
(4)のベクトル図より,二次側換算した等式は,
\[
\begin{eqnarray}
V_{\mathrm {20}}&=&\sqrt {\left( V_{\mathrm {2n}}+RI_{\mathrm {2n}}\cos \theta +XI_{\mathrm {2n}}\sin \theta \right) ^{2} +\left( XI_{\mathrm {2n}}\cos \theta -RI_{\mathrm {2n}}\sin \theta \right) ^{2}} \\[ 5pt ]
&=&V_{\mathrm {2n}}\sqrt {\left( 1+\frac {RI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\cos \theta +\frac {XI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\sin \theta \right) ^{2} +\left( \frac {XI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\cos \theta -\frac {RI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\sin \theta \right) ^{2}} \\[ 5pt ]
&=&V_{\mathrm {2n}}\sqrt {\left( 1+q_{\mathrm {R}}\cos \theta +q_{\mathrm {X}}\sin \theta \right) ^{2} +\left( q_{\mathrm {X}}\cos \theta -q_{\mathrm {R}}\sin \theta \right) ^{2}} \\[ 5pt ]
&=&V_{\mathrm {2n}}\sqrt {1+q_{\mathrm {R}}^{2}\cos ^{2}\theta +q_{\mathrm {X}}^{2}\sin ^{2}\theta +2q_{\mathrm {R}}\cos \theta +2q_{\mathrm {R}}q_{\mathrm {X}}\cos \theta \sin \theta +2q_{\mathrm {X}}\sin \theta +q_{\mathrm {X}}^{2}\cos ^{2}\theta -2q_{\mathrm {R}}q_{\mathrm {X}}\cos \theta \sin \theta +q_{\mathrm {R}}^{2}\sin ^{2}\theta } \\[ 5pt ]
&=&V_{\mathrm {2n}}\sqrt {1+q_{\mathrm {R}}^{2}+q_{\mathrm {X}}^{2}+2q_{\mathrm {R}}\cos \theta +2q_{\mathrm {X}}\sin \theta } \\[ 5pt ]
&≒&V_{\mathrm {2n}}\sqrt {1+2q_{\mathrm {R}}\cos \theta +2q_{\mathrm {X}}\sin \theta } \\[ 5pt ]
&≒&V_{\mathrm {2n}}\left( 1+q_{\mathrm {R}}\cos \theta +q_{\mathrm {X}}\sin \theta \right)
\end{eqnarray}
\]
となる。よって電圧変動率\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon&=&\frac {V_{\mathrm {20}}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&=&\frac {V_{\mathrm {2n}}\left( 1+q_{\mathrm {R}}\cos \theta +q_{\mathrm {X}}\sin \theta \right)-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&=&\left( q_{\mathrm {R}}\cos \theta +q_{\mathrm {X}}\sin \theta \right)\times 100 [%] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは