《機械・制御》〈自動制御〉[H29:問4]RLC直列回路の伝達関数に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

図1に示す\( \ RLC \ \)直列回路において，電圧\( \ v_{\mathrm {i}}(t) \ \)を入力信号，電圧\( \ v_{\mathrm {o}}(t) \ \)を出力信号とみなすとき，次の問に答えよ。ただし，全ての変数の初期値は零とする。

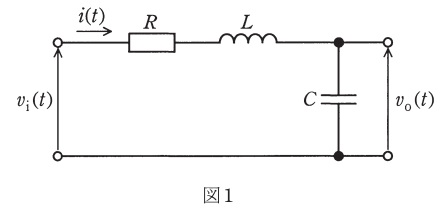
\( \ v_{\mathrm {i}}(t) \ \)のラプラス変換\( \ V_{\mathrm {i}}(s) \ \)を入力，\( \ v_{\mathrm {o}}(t) \ \)のラプラス変換\( \ V_{\mathrm {o}}(s) \ \)を出力とするブロック線図を図2に示す。このブロックに当てはまる伝達関数\( \ G(s) \ \)を以下の手順で求めよ。

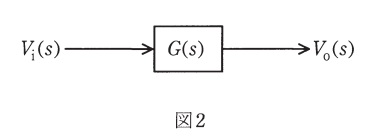
(1)　回路に流れる電流を\( \ i(t) \ \)として，コンデンサの両端にかかる電圧\( \ v_{\mathrm {o}}(t) \ \)を求めよ。求めた関係式をラプラス変換せよ。\( \ i(t) \ \)をラプラス変換したものを\( \ I(s) \ \)で表し，\( \ V_{\mathrm {o}}(s) \ \)を入力，\( \ I(s) \ \)を出力とするブロック線図で表せ。

(2)　抵抗及びコイルそれぞれの両端にかかる電圧と\( \ v_{\mathrm {o}}(t) \ \)の和が\( \ v_{\mathrm {i}}(t) \ \)である。この関係式をラプラス変換して，\( \ I(s) \ \)及び\( \ V_{\mathrm {o}}(s) \ \)を入力，\( \ V_{\mathrm {i}}(s) \ \)を出力とするブロック線図で示せ。

(3)　上記小問(1)及び(2)で求めたブロック線図を用いて，\( \ V_{\mathrm {o}}(s) \ \)を入力，\( \ V_{\mathrm {i}}(s) \ \)を出力とする\( \ RLC \ \)直列回路全体のブロック線図をを求めよ。

(4)　小問(3)で求めたブロック線図を等価変換することで，\( \ V_{\mathrm {i}}(s) \ \)を入力，\( \ V_{\mathrm {o}}(s) \ \)を出力とする図2に示すような一つのブロックに簡略化せよ。

(5)　\( \ V_{\mathrm {i}}(s) \ \)から\( \ V_{\mathrm {o}}(s) \ \)までの伝達関数は2次遅れ系となる。\( \ R=\mathrm {1 \ \Omega } \ \)，\( \ L=\mathrm {2 \ mH} \ \)，\( \ C=\mathrm {500 \ \mu F} \ \)であるときの固有角周波数\( \ \omega _{\mathrm {n}} \ [\mathrm {rad/s}] \ \)及び減衰係数\( \ \zeta \ \)をそれぞれ求めよ。

【ワンポイント解説】

本問は小問が多いため，スムースに解かないと時間切れになってしまいます。しかし，比較的取り組みやすい問題なので，よく理解して解けるようにしておきましょう。

1.微分と積分のラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると，
\[
\begin{eqnarray}
\mathcal{L}[f^{’}(t)]&=&sF(s)-f(0) \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
\mathcal{L}\left[ \int ^{t}_{0}f(\tau )d\tau \right] &=&\frac {1}{s}F(s) \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)
コンデンサの初期電荷を\( \ 0 \ \)とし，時間\( \ t \ \)で蓄えられた電荷\( \ Q(t) \ \)とすると，
\[
\begin{eqnarray}
v_{\mathrm {o}}(t) &=& \frac {Q(t)}{C} \\[ 5pt ] &=& \frac {1}{C}\int ^{t}_{0}i(\tau )d\tau \\[ 5pt ] \end{eqnarray}
\] となるから，両辺ラプラス変換すると，
\[
\begin{eqnarray}
V_{\mathrm {o}}(s) &=& \frac {1}{C}\cdot \frac {1}{s}I(s) \\[ 5pt ] &=& \frac {1}{Cs}I(s) \\[ 5pt ] \end{eqnarray}
\] となる。ゆえに，
\[
\begin{eqnarray}
I(s)&=&CsV_{\mathrm {o}}(s) \\[ 5pt ] \end{eqnarray}
\] となるから，ブロック線図は図3のようになる。

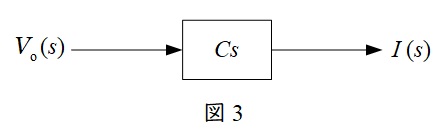
(2)
題意より，回路方程式は，
\[
\begin{eqnarray}
v_{\mathrm {i}}(t)&=&Ri(t)+L\frac {di}{dt}+v_{\mathrm {o}}(t) \\[ 5pt ] \end{eqnarray}
\] となるから，両辺をラプラス変換すると，
\[
\begin{eqnarray}
V_{\mathrm {i}}(s)&=&RI(s)+LsI(s)-Li(0)+V_{\mathrm {o}}(s) \\[ 5pt ] \end{eqnarray}
\] となる。電流の初期値を\( \ 0 \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {i}}(s)&=&(R+Ls)I(s)+V_{\mathrm {o}}(s) \\[ 5pt ] \end{eqnarray}
\] と求められるので，ブロック線図は図4のようになる。

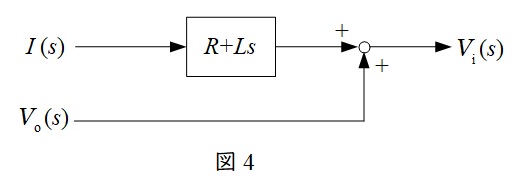
(3)
(1)，(2)より(1)の出力\( \ I(s) \ \)を(2)の入力に入れれば良いので，図5のようになる。

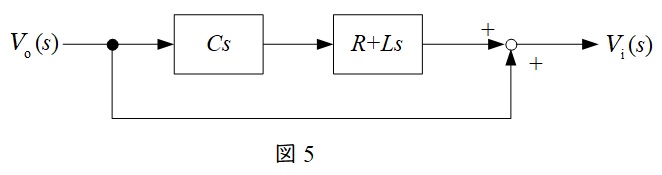
(4)
図5の回路を等価変換すると図6になる。

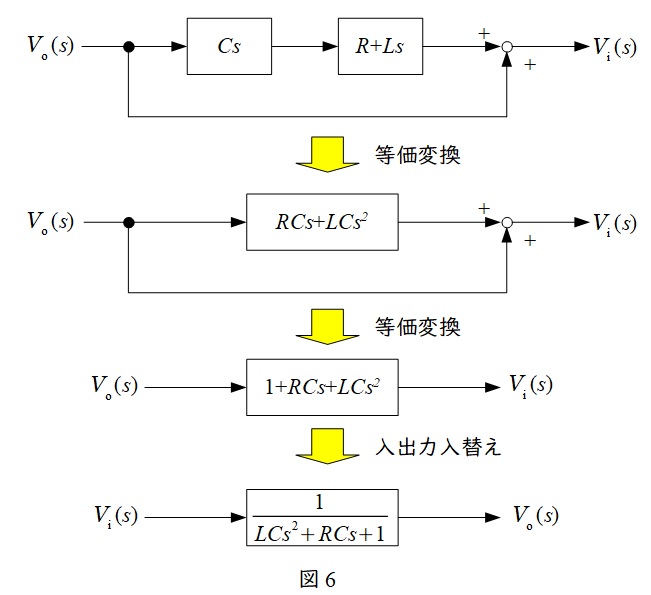
(5)
図6の回路の伝達関数を\( \ W(s) \ \)とおいて，各値を代入すると，
\[
\begin{eqnarray}
W(s) &=& \frac {1}{LCs^{2}+RCs+1} \\[ 5pt ] &=& \frac {1}{2\times 10^{-3}\times 500\times 10^{-6}s^{2}+1\times 500\times 10^{-6}s+1} \\[ 5pt ] &=& \frac {1}{10^{-6}s^{2}+500\times 10^{-6}s+1} \\[ 5pt ] &=& \frac {10^{6}}{s^{2}+500s+10^{6}}
\end{eqnarray}
\] となる。ここで，\( \ 2 \ \)次遅れ系の伝達関数は，
\[
\begin{eqnarray}
W(s) &=& \frac {{\omega _{\mathrm {n}}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}} s+{\omega _{\mathrm {n}}}^{2}} \\[ 5pt ] \end{eqnarray}
\] と表されるから，係数を比較すると，
\[
\begin{eqnarray}
{\omega _{\mathrm {n}}}^{2}&=&10^{6}，2\zeta \omega _{\mathrm {n}}&=&500 \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
\omega _{\mathrm {n}}&=&10^{3} \ \mathrm {[rad/s]}，\zeta&=&0.25 \\[ 5pt ] \end{eqnarray}
\] と求められる。