《機械・制御》〈回転機〉[R04:問1]三相同期発電機の短絡比及び電圧変動率に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

同期発電機に関して，次の問に答えよ。

定格電圧\( \ 6 \ 000 \ \mathrm {V} \ \)，容量\( \ 5 \ 000 \ \mathrm {kV\cdot A} \ \)の三相同期発電機がある。無負荷で定格電圧を発生させる界磁電流における三相短絡電流は\( \ 300 \ \mathrm {A} \ \)であった。この発電機について次の問に答えよ。なお，巻線抵抗は無視し，定格力率は\( \ 90 \ \mathrm {％} \ \)とする。また，磁気飽和は無視する。

(1)　定格電流\( \ I_{\mathrm {N}} \ \mathrm {[A]} \ \)を求めよ。

(2)　短絡比\( \ K \ \)を求めよ。

(3)　基準インピーダンス\( \ Z_{\mathrm {N}} \ \mathrm {[\Omega ]} \ \)を求めよ。

(4)　同期リアクタンス\( \ Z_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)を求めよ。

(5)　定格状態で運転しているときの電圧変動率\( \ \varepsilon \ \mathrm {[％]} \ \)を求めよ。

【ワンポイント解説】

同期発電機の諸計算に関する問題です。
(5)の計算量がやや多めですが，全体的には取り組みやすい問題です。
同期機における重要な内容を多く扱っている問題なので，本問に関しては本番までに完答できるように勉強を進めて下さい。

1.同期発電機の等価回路
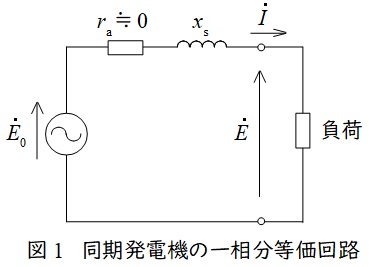
同期発電機の一相分等価回路は誘導起電力（相電圧）\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)，端子電圧（相電圧）\( \ \dot E \ \mathrm {[V]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。
通常，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は十分に小さいと考え，無視して考えることが一般的です。
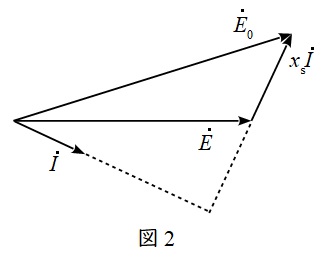
また，等価回路よりベクトル図は図2のようになります。

2.同期発電機の無負荷飽和曲線と三相短絡曲線
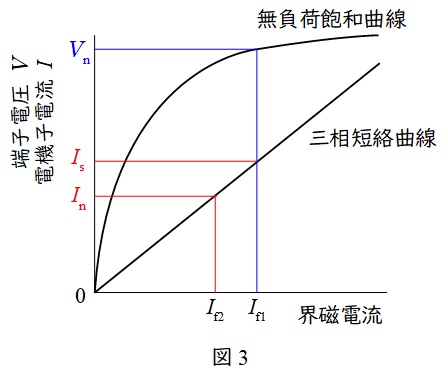
同期発電機は図3のような無負荷飽和曲線と三相短絡曲線の特性があります。図中の\( \ V_{\mathrm {n}} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \)は定格電流，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.電圧変動率
同期発電機において，無負荷時の端子電圧を\( \ V_{0} \ \)，定格負荷時の端子電圧を\( \ V_{\mathrm {n}} \ \)とすると，電圧変動率\( \ \varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{0}-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] で定義されます。

4.オーム法から単位法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}　　 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z \ \mathrm {[\Omega ]} \ }{V_{\mathrm {n}}^{2}}　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

5.単位法における三相短絡電流計算
単位法における故障点から電源側を見た線路のインピーダンスを\( \ Z_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)とすると，三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※単位法の定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ] &=&\frac {I_{\mathrm {n}}}{Z_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)定格電流\( \ I_{\mathrm {N}} \ \mathrm {[A]} \ \)
定格容量\( \ P_{\mathrm {N}}= 5 \ 000 \ \mathrm {[kV\cdot A]} \ \)，定格電圧\( \ V_{\mathrm {N}}= 6 \ 000 \ \mathrm {[V]} \ \)であるから，定格電流\( \ I_{\mathrm {N}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {N}}&=&\sqrt {3}V_{\mathrm {N}}I_{\mathrm {N}} \\[ 5pt ] I_{\mathrm {N}}&=&\frac {P_{\mathrm {N}}}{\sqrt {3}V_{\mathrm {N}}} \\[ 5pt ] &=&\frac {5 \ 000\times 10^{3}}{\sqrt {3}\times 6 \ 000} \\[ 5pt ] &≒&481.13　→　481 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)短絡比\( \ K \ \)
題意より，定格運転時の三相短絡電流\( \ I_{\mathrm {S}}=300 \ \mathrm {[A]} \ \)なので，短絡比\( \ K \ \)は，ワンポイント解説「2.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {S}}}{I_{\mathrm {N}}} \\[ 5pt ] &=& \frac {300}{481.13} \\[ 5pt ] &≒&0.62353　→　0.624 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)基準インピーダンス\( \ Z_{\mathrm {N}} \ \mathrm {[\Omega ]} \ \)
基準インピーダンス\( \ Z_{\mathrm {N}} \ \mathrm {[\Omega ]} \ \)は，オームの法則より，
\[
\begin{eqnarray}
Z_{\mathrm {N}} &=& \frac {V_{\mathrm {N}}}{\sqrt {3}I_{\mathrm {N}}} \\[ 5pt ] &=& \frac {6 \ 000}{\sqrt {3}\times 481.13} \\[ 5pt ] &≒&7.1999　→　7.20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)同期リアクタンス\( \ Z_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)
同期リアクタンス\( \ Z_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)は，三相短絡事故発生時のリアクタンスに相当するから，ワンポイント解説「5.単位法における三相短絡電流計算」の通り，
\[
\begin{eqnarray}
Z_{\mathrm {S}} &=& \frac {V_{\mathrm {N}}}{\sqrt {3}I_{\mathrm {S}}} \\[ 5pt ] &=& \frac {6 \ 000}{\sqrt {3}\times 300} \\[ 5pt ] &≒&11.547　→　11.5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)定格状態で運転しているときの電圧変動率\( \ \varepsilon \ \mathrm {[％]} \ \)
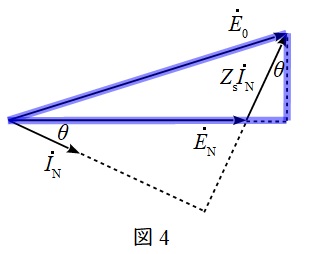
題意に沿ってベクトル図を描くと図4のようになる。ただし，\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)は無負荷時の誘導起電力（相電圧），\( \ {\dot E}_{\mathrm {N}} \ \mathrm {[V]} \ \)は定格電圧（相電圧），\( \ \theta \ \)は力率角である。
図4に示す三角形に三平方の定理を適用すると，
\[
\begin{eqnarray}
E_{0} &=& \sqrt {\left( E_{\mathrm {N}}+Z_{\mathrm {S}}I_{\mathrm {N}}\sin \theta \right) ^{2}+\left( Z_{\mathrm {S}}I_{\mathrm {N}}\cos \theta \right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があり，
\[
\begin{eqnarray}
\sin \theta &=& \sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=& \sqrt {1-0.9 ^{2}} \\[ 5pt ] &≒& 0.43589 \\[ 5pt ] \end{eqnarray}
\] であるから，各値を代入すると，
\[
\begin{eqnarray}
E_{0} &=& \sqrt {\left( E_{\mathrm {N}}+Z_{\mathrm {S}}I_{\mathrm {N}}\sin \theta \right) ^{2}+\left( Z_{\mathrm {S}}I_{\mathrm {N}}\cos \theta \right) ^{2}} \\[ 5pt ] &=& \sqrt {\left( \frac {6 \ 000}{\sqrt {3}}+11.547\times 481.13\times 0.43589 \right) ^{2}+\left( 11.547\times 481.13\times 0.9 \right) ^{2}} \\[ 5pt ] &≒& \sqrt {5885.7 ^{2}+5000.0 ^{2}} \\[ 5pt ] &≒& 7722.8 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，電圧変動率\( \ \varepsilon \ \mathrm {[％]} \ \)は，ワンポイント解説「3.電圧変動率」の通り，
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{0}-V_{\mathrm {N}}}{V_{\mathrm {N}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}E_{0}-V_{\mathrm {N}}}{V_{\mathrm {N}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}\times 7722.8-6000}{6000}\times 100 \\[ 5pt ] &≒&123 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。