【問題】
【難易度】★☆☆☆☆(易しい)
定格容量\( \ 300 \ \mathrm {[kV\cdot A]} \ \),定格一次電圧\( \ 6 \ 600 \ \mathrm {[V]} \ \),定格二次電圧\( \ 440 \ \mathrm {[V]} \ \),定格周波数\( \ 60 \ \mathrm {[Hz]} \ \)の単相変圧器がある。この変圧器の二次側の端子を開放して,一次側に定格周波数,定格一次電圧を印加したところ,一次側に\( \ 0.483 \ \mathrm {[A]} \ \)の電流が流れ,力率は\( \ 0.325 \ \)(遅れ)であった。
また,負荷力率\( \ 1 \ \)で運転したとき,定格容量の\( \ 30 \ \mathrm {[%]} \ \)負荷時の効率と定格容量の\( \ 70 \ \mathrm {[%]} \ \)負荷時の効率とが等しくなった。
この変圧器について,次の値を求めよ。ただし,損失は鉄損と銅損以外は無視できるものとする。
(1) 鉄損 \( \ \mathrm {[W]} \ \)
(2) 定格負荷で運転したときの銅損 \( \ \mathrm {[W]} \ \)
(3) 負荷力率\( \ 1 \ \)で負荷率を変えて運転したときの最大効率 \( \ \mathrm {[%]} \ \)
【ワンポイント解説】
単相変圧器の損失と効率に関する問題です。
計算量もあまり多くなく,比較的考えやすい問題なので,多くの受験生が選択したと考えられます。
このような問題を選択し,計算間違いをせず完答できると合格に一気に近づくことになります。
1.変圧器の等価回路(一次換算)と鉄損及び銅損
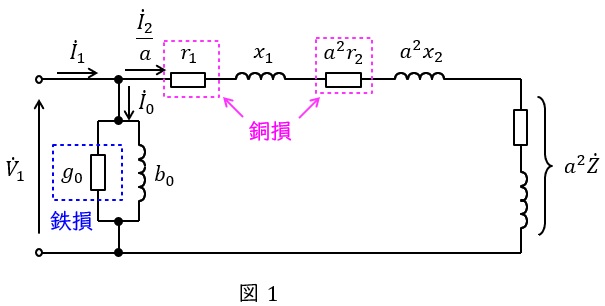
変圧器の一次側換算等価回路を図1に示します。ただし,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス,\( \ g_{0} \ \mathrm {[S]} \ \)は励磁コンダクタンス,\( \ b_{0} \ \mathrm {[S]} \ \)は励磁サセプタンス,\( \ a \ \)は変圧比(巻数比)となります。
等価回路より,鉄損は電圧\( \ {\dot V}_{1} \ \)の\( \ 2 \ \)乗に比例し,銅損は電流\( \ {\dot I}_{2} \ \)の\( \ 2 \ \)乗に比例することがわかります。
2.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)
変圧器の損失は鉄損\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)と銅損\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)があり,\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)は負荷によらず一定であり,\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)は負荷(電流)の\( \ 2 \ \)乗に比例します。従って,定格出力\( \ P_{\mathrm {n}} \ \mathrm {[W]} \ \)で利用率\( \ \alpha \ \)の時の変圧器の効率\( \ \eta \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ]
&=&\frac {出力}{出力+損失} \\[ 5pt ]
&=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
次に,最大効率\( \ \eta _{\mathrm {m}} \ \)を求めます。上式の分母分子を\( \ \alpha \ \)で割ると
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,効率が最大となるためには,上式の分母が最小となれば良いです。よって,\( \ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ \)と置くと,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ \)となるとき,\( \ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ \)であり,鉄損と銅損が等しい時効率は最大となります。
※ 本問においては,鉄損と銅損が等しい時,効率が最大となることを覚えていれば問題ありません。
【関連する「電気の神髄」記事】
【解答】
(1)鉄損 \( \ \mathrm {[W]} \ \)
図1の等価回路に示すように,二次側の端子を開放して,一次側に電圧を印加した場合,電流が流れるのは励磁回路のみであり,このとき発生するのは鉄損である。
したがって鉄損\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)は,定格一次電圧\( \ V_{1}= 6 \ 600 \ \mathrm {[V]} \ \)を印加したときに一次側に\( \ I_{0}=0.483 \ \mathrm {[A]} \ \)が流れ,そのときの力率が\( \ \cos \theta =0.325 \ \)であるから,
\[
\begin{eqnarray}
p_{\mathrm {i}} &=&V_{1}I_{0}\cos \theta \\[ 5pt ]
&=&6 \ 600\times 0.483\times 0.325 \\[ 5pt ]
&≒&1 \ 036.0 → 1 \ 040 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)定格負荷で運転したときの銅損 \( \ \mathrm {[W]} \ \)
定格負荷時の銅損\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)とする。
力率\( \ 1 \ \)で運転したとき,定格容量\( \ P_{\mathrm {n}}=300 \ \mathrm {[kV\cdot A]} \ \)の\( \ 30 \ \mathrm {[%]} \ \)負荷時の効率と定格容量の\( \ 70 \ \mathrm {[%]} \ \)負荷時の効率が等しいことから,ワンポイント解説「2.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)」の通り,
\[
\begin{eqnarray}
\frac {0.3\times P_{\mathrm {n}}}{0.3\times P_{\mathrm {n}}+p_{\mathrm {i}}+0.3 ^{2}\times p_{\mathrm {c}}}&=&\frac {0.7\times P_{\mathrm {n}}}{0.7\times P_{\mathrm {n}}+p_{\mathrm {i}}+0.7 ^{2}\times p_{\mathrm {c}}} \\[ 5pt ]
\frac {0.3\times 300\times 10^{3}}{0.3\times 300\times 10^{3}+1 \ 036.0+0.3 ^{2}\times p_{\mathrm {c}}}&=&\frac {0.7\times 300\times 10^{3}}{0.7\times 300\times 10^{3}+1 \ 036.0+0.7 ^{2}\times p_{\mathrm {c}}} \\[ 5pt ]
\frac {0.3}{0.3\times 300\times 10^{3}+1 \ 036.0+0.3 ^{2}\times p_{\mathrm {c}}}&=&\frac {0.7}{0.7\times 300\times 10^{3}+1 \ 036.0+0.7 ^{2}\times p_{\mathrm {c}}} \\[ 5pt ]
0.3\times \left( 0.7\times 300\times 10^{3}+1 \ 036.0+0.7 ^{2}\times p_{\mathrm {c}}\right) &=&0.7\times \left( 0.3\times 300\times 10^{3}+1 \ 036.0+0.3 ^{2}\times p_{\mathrm {c}}\right) \\[ 5pt ]
0.21\times 300\times 10^{3}+310.8+0.147\times p_{\mathrm {c}} &=&0.21\times 300\times 10^{3}+725.2+0.063\times p_{\mathrm {c}} \\[ 5pt ]
310.8+0.147\times p_{\mathrm {c}} &=&725.2+0.063\times p_{\mathrm {c}} \\[ 5pt ]
0.084p_{\mathrm {c}} &=&414.4 \\[ 5pt ]
p_{\mathrm {c}} &≒&4 \ 933.3 → 4 \ 930 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)負荷力率\( \ 1 \ \)で負荷率を変えて運転したときの最大効率 \( \ \mathrm {[%]} \ \)
最大効率時の負荷率を\( \ \alpha _{\mathrm {m}} \ \)とすると,ワンポイント解説「2.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)」の通り,鉄損と銅損が等しいとき最大効率となるから,
\[
\begin{eqnarray}
p_{\mathrm {i}}&=&{\alpha _{\mathrm {m}}}^{2}p_{\mathrm {c}} \\[ 5pt ]
{\alpha _{\mathrm {m}}}^{2}&=&\frac {p_{\mathrm {i}}}{p_{\mathrm {c}}} \\[ 5pt ]
\alpha _{\mathrm {m}}&=&\sqrt {\frac {p_{\mathrm {i}}}{p_{\mathrm {c}}}} \\[ 5pt ]
&=&\sqrt {\frac {1 \ 036.0}{4 \ 933.3}} \\[ 5pt ]
&≒&0.45826 \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,最大効率\( \ \eta _{\mathrm {m}} \ \mathrm {[%]} \ \)は,ワンポイント解説「2.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)」の通り,
\[
\begin{eqnarray}
\eta _{\mathrm {m}} &=&\frac {\alpha _{\mathrm {m}}P_{\mathrm {n}}}{\displaystyle \alpha _{\mathrm {m}}P_{\mathrm {n}}+p_{\mathrm {i}}+{\alpha _{\mathrm {m}}}^{2} p_{\mathrm {c}}} \\[ 5pt ]
&=&\frac {\alpha _{\mathrm {m}}P_{\mathrm {n}}}{\displaystyle \alpha _{\mathrm {m}}P_{\mathrm {n}}+2p_{\mathrm {i}}} \\[ 5pt ]
&=&\frac {0.45826\times 300\times 10^{3}}{\displaystyle 0.45826\times 300\times 10^{3}+2\times 1 \ 036.0} \\[ 5pt ]
&≒&0.985 → 98.5 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは