Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,平行平板コンデンサに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は数値(最も近い数値)を解答群の中から選び,その記号をマークシートに記入しなさい。
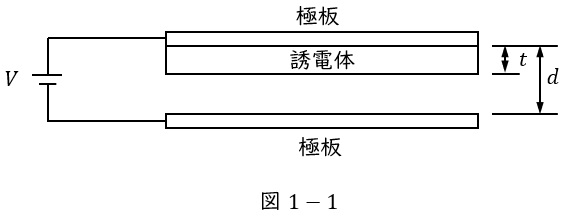
図1のように,真空中に平行平板コンデンサがある(図は横から見た図である)。このコンデンサの各極板は一辺の長さが\( \ a \ \)の正方形の導体平板である。その極板間の距離は\( \ d \ \)で,その中に極板と同形で厚さ\( \ t \ \),比誘電率\( \ \varepsilon _{r} \ \)の誘電体が極板に平行に入っている。また,真空の誘電率を\( \ \varepsilon _{0} \ \)とし,電束は一様に分布しており端効果はないものとする。
このコンデンサの静電容量(キャパシタンス)は,\( \ \fbox { (1) } \ \)である。この平行平板コンデンサの極板間に電圧\( \ V \ \)を印加したとき,極板間における電束密度は\( \ \fbox { (2) } \ \)であり,誘電体部分の電界は\( \ \fbox { (3) } \ \)である。また,このコンデンサに蓄えられる総エネルギーは\( \ \fbox { (4) } \ \)である。
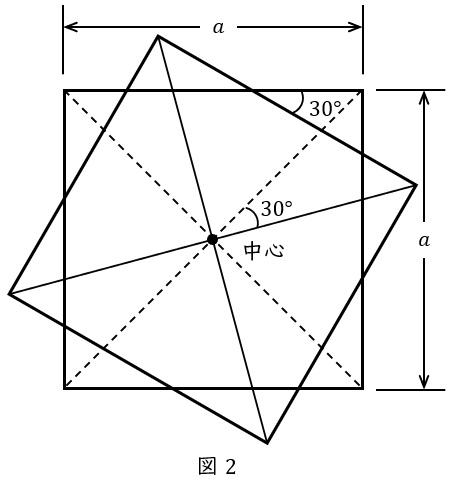
次に,片方の極板のみを図2のように極板の対角線の交点を中心として\( \ 30 \ \)度回転させた場合,静電容量は回転させない場合の\( \ \fbox { (5) } \ \)倍となる。ただし,極板の幾何学的な重なり部分にのみ静電容量があるものとする。また,図2において,回転によりできる周囲の直角三角形はすべて合同である。

〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\varepsilon _{0}\varepsilon _{r}a^{2}}{\left( d-t\right) \varepsilon _{r}+t} &(ロ)& \frac {\varepsilon _{0}\varepsilon _{r}V}{\left( d-t\right) \varepsilon _{0}+t} &(ハ)& 0.85 \\[ 5pt ]
&(ニ)& \frac {1}{2}\cdot \frac {\varepsilon _{0}\varepsilon _{r}a^{2}V}{\left( d-t\right) \varepsilon _{r}+t} &(ホ)& \frac {1}{2}\cdot \frac {\varepsilon _{0}\varepsilon _{r}a^{2}V^{2}}{\left( d-t\right) \varepsilon _{r}+t} &(ヘ)& \frac {\varepsilon _{0}\varepsilon _{r}}{\left( d-t\right) \varepsilon _{r}+t} \\[ 5pt ]
&(ト)& \frac {\varepsilon _{0}\varepsilon _{r}a^{2}V^{2}}{\left( d-t\right) \varepsilon _{r}+t} &(チ)& \frac {\varepsilon _{0}\varepsilon _{r}V}{\left( d-t\right) \varepsilon _{r}+t} &(リ)& \frac {\varepsilon _{r}a^{2}}{\left( d-t\right) \varepsilon _{0}+t} \\[ 5pt ]
&(ヌ)& \frac {1}{\left( d-t\right) \varepsilon _{r}+t} &(ル)& 1.20 &(ヲ)& \frac {\varepsilon _{0}a^{2}}{\left( d-t\right) \varepsilon _{r}+t} \\[ 5pt ]
&(ワ)& 0.79 &(カ)& \frac {V}{\left( d-t\right) \varepsilon _{r}+t} &(ヨ)& \frac {V}{\left( d-t\right) \varepsilon _{0}+t} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
誘電体を挿入した平行平板コンデンサの各諸量を求める問題です。
電験三種よりも高度な問題となっているのは(5)の空欄で,他の空欄はできれば正答しておきたい問題です。
基本公式をきっちりとマスターして,確実に計算するようにして下さい。
1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて,蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には,
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \),極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \),極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.コンデンサの合成静電容量
静電容量\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)の合成静電容量\( \ C \ \mathrm {[F]} \ \)は,
並列接続時:\( \ C=C_{1}+C_{2} \ \)
直列接続時:\( \ \displaystyle C=\frac {1}{\displaystyle \frac {1}{C_{1}}+\frac {1}{C_{2}}}=\frac {C_{1}C_{2}}{C_{1}+C_{2}} \ \)
となります。
4.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると,極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
5.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係
極板間の誘電率を\( \ \varepsilon \ \mathrm {[F / m]} \ \)とすると,電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)と電界\( \ E \ \mathrm {[V / m]} \ \)には,
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \),誘電体の比誘電率を\( \ \varepsilon _{\mathrm {r}} \ \)とすると,\( \ \varepsilon = \varepsilon _{\mathrm {r}}\varepsilon _{0} \ \)の関係があるので,
\[
\begin{eqnarray}
D&=&\varepsilon _{\mathrm {r}}\varepsilon _{0}E \\[ 5pt ]
\end{eqnarray}
\]
となります。
6.平行平板コンデンサの静電エネルギー\( \ W \ \)
平行平板コンデンサの静電エネルギー\( \ W \ \mathrm {[J]} \ \)は,
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ Q=CV \ \)の関係から,
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ]
&=&\frac {Q^{2}}{2C} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:イ
誘電体の挿入位置によらず静電容量は変わらないため,図1-1のように考えると誘電体部及び真空部の静電容量\( \ C_{1} \ \)及び\( \ C_{2} \ \)は,ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り,
\[
\begin{eqnarray}
C_{1} &=&\frac {\varepsilon _{r} \varepsilon _{0}a^{2}}{t} \\[ 5pt ]
C_{2} &=&\frac {\varepsilon _{0}a^{2}}{d-t} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,コンデンサ全体の静電容量\( \ C \ \)は,ワンポイント解説「3.コンデンサの合成静電容量」の通り,
\[
\begin{eqnarray}
C &=&\frac {1}{\displaystyle \frac {1}{C_{1}}+\frac {1}{C_{2}}} \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {t}{\varepsilon _{r} \varepsilon _{0}a^{2}}+\frac {d-t}{\varepsilon _{0}a^{2}}} \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {t+\varepsilon _{r}\left( d-t\right) }{\varepsilon _{r} \varepsilon _{0}a^{2}}} \\[ 5pt ]
&=&\frac {\varepsilon _{r} \varepsilon _{0}a^{2}}{t+\varepsilon _{r}\left( d-t\right) } \\[ 5pt ]
&=&\frac {\varepsilon _{0}\varepsilon _{r}a^{2}}{\left( d-t\right) \varepsilon _{r}+t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
電荷\( \ Q \ \)から出る電束は\( \ Q \ \)であり,電束密度\( \ D \ \)は平行平板コンデンサにおいては極板の単位面積あたりの電束を考えればよい。したがって,ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り,
\[
\begin{eqnarray}
D &=&\frac {Q}{a^{2}} \\[ 5pt ]
&=&\frac {CV}{a^{2}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {\varepsilon _{0}\varepsilon _{r}a^{2}}{\left( d-t\right) \varepsilon _{r}+t}V}{a^{2}} \\[ 5pt ]
&=&\frac {\varepsilon _{0}\varepsilon _{r}V}{\left( d-t\right) \varepsilon _{r}+t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:カ
誘電体部分の電界\( \ E_{1} \ \)は,ワンポイント解説「5.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係」の通り,
\[
\begin{eqnarray}
E_{1} &=&\frac {D}{\varepsilon _{0}\varepsilon _{r}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {\varepsilon _{0}\varepsilon _{r}V}{\left( d-t\right) \varepsilon _{r}+t}}{\varepsilon _{0}\varepsilon _{r}} \\[ 5pt ]
&=&\frac {V}{\left( d-t\right) \varepsilon _{r}+t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ホ
コンデンサに蓄えられる総エネルギー\( \ W \ \)は,ワンポイント解説「6.平行平板コンデンサの静電エネルギー\( \ W \ \)」の通り,
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ]
&=&\frac {1}{2}\cdot \frac {\varepsilon _{0}\varepsilon _{r}a^{2}}{\left( d-t\right) \varepsilon _{r}+t} \cdot V^{2} \\[ 5pt ]
&=&\frac {1}{2}\cdot \frac {\varepsilon _{0}\varepsilon _{r}a^{2}V^{2}}{\left( d-t\right) \varepsilon _{r}+t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
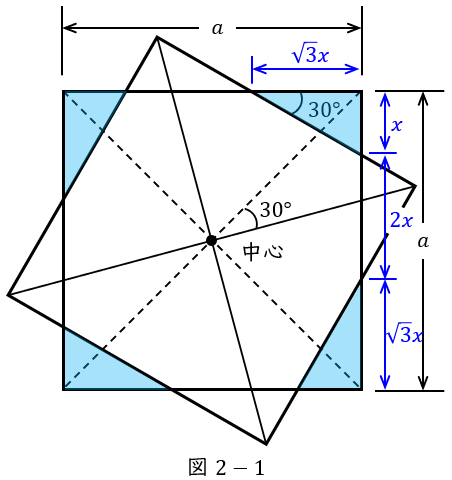
(5)解答:ハ
図2-1に示すように,回転させた後の重ならない部分の最も短い辺を\( \ x \ \)とすると,直角三角形の関係より各辺の長さは図2-1に示すようになる。したがって,
\[
\begin{eqnarray}
a&=&x+2x+\sqrt {3}x \\[ 5pt ]
&=&\left( 3+\sqrt {3}\right) x \\[ 5pt ]
x&=&\frac {a}{3+\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
の関係がある。\( \ 30 \ \)度回転させた後の重なり合う極板面積は,図2-1に示した部分の面積を差し引いた分だけ小さくなるので,
\[
\begin{eqnarray}
a^{2}-\frac {x\cdot \sqrt {3}x}{2}\times 4 &=&a^{2}-2\sqrt {3}x^{2} \\[ 5pt ]
&=&a^{2}-2\sqrt {3}\left( \frac {a}{3+\sqrt {3}}\right) ^{2} \\[ 5pt ]
&≒&a^{2}-0.154 \ 7a^{2} \\[ 5pt ]
&≒&0.845 \ 3a^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り,平行平板コンデンサの静電容量は重なり合う極板面積に比例するので,静電容量は約\( \ 0.85 \ \)倍と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは