《理論》〈電磁気〉[H20:問2]空隙を含む磁気回路のインダクタンスに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，鉄心入り巻線のインダクタンスに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式，数値（最も近い数値）又は図を解答群の中から選び，その記号をマークシートに記入しなさい。

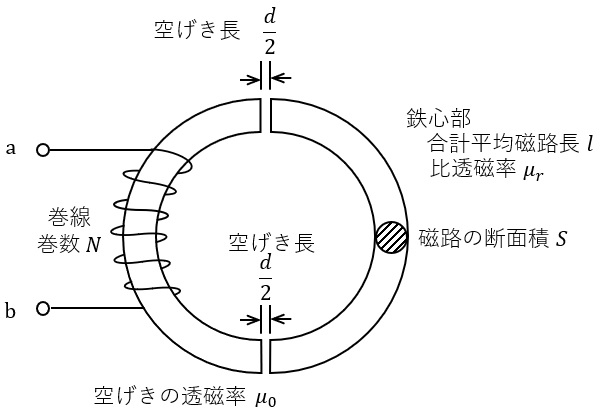
図のように，鉄心部と空げき部からなる磁路に，巻数$ \ N \ $の巻線が巻かれている。鉄心部は，左右合計の平均磁路長$ \ l \ $，比透磁率$ \ \mu _{r} \ $の鉄心から成っている。二つある空げき部は同寸法であり，それらの合計の空げき長を$ \ d \ $とし，空げきの透磁率は真空の透磁率$ \ \mu _{0} \ $に等しいものとする。磁路の断面積は，鉄心部と空げき部ともに$ \ S \ $である。磁路において磁束は一様に分布し，漏れ磁束，磁気飽和，ヒステリシス，渦電流はないものとする。

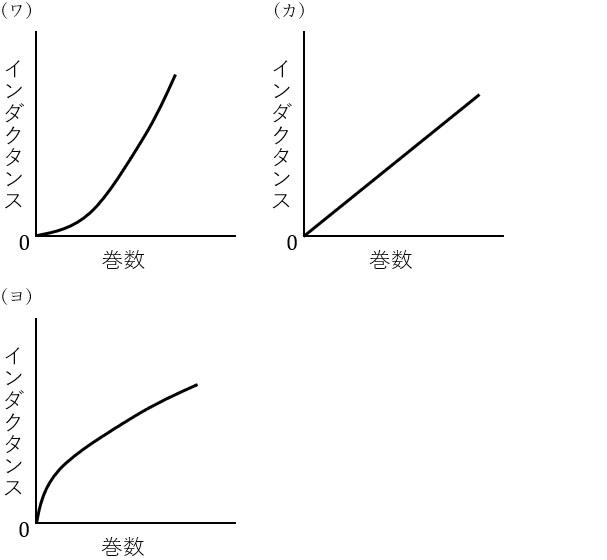
図の巻線において，磁路の磁気抵抗は$ \ \fbox {　（１）　} \ $であり，インダクタンスは$ \ \fbox {　（２）　} \ $である。また，巻線の巻数に対するインダクタンスの関係を表す概略図は$ \ \fbox {　（３）　} \ $となる。

次に，この巻線と磁路の定数を
\[
\begin{eqnarray}
N &=&100,l=250 \ \mathrm {[mm]}, d=0.8 \ \mathrm {[mm]}, S=600 \ \mathrm {[{mm}^{2}]}, \\[ 5pt ] \mu _{0}&=&4\pi \times 10^{-7} \ \mathrm{[H / m]},\mu _{r} = 2 \ 000 \\[ 5pt ] \end{eqnarray}
\] とし，このときの巻線のインダクタンスを$ \ L_{0} \ $とする。

いま，鉄心部の寸法及び透磁率を変更しないで巻線のインダクタンスを$ \ L_{0} \ $の$ \ 4 \ $倍とするためには，次の二つの方法が考えられる。

①　巻数のみを変える場合，$ \ N \ $の$ \ \fbox {　（４）　} \ $倍となる巻数に変更する。
②　空げき長のみを変える場合，$ \ d \ $の$ \ \fbox {　（５）　} \ $倍となる空げき長に調整する。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\mu S}{l}+\frac {\mu _{r}\mu _{0}S}{d}　　　　　&（ロ）&　0.33　　　　　&（ハ）&　16 \\[ 5pt ] &（ニ）&　4　　　　　&（ホ）&　2　　　　　&（ヘ）&　0.13 \\[ 5pt ] &（ト）&　\frac {l}{\mu _{r}S}+\frac {d}{\mu _{0}S}　　　　　&（チ）&　\frac {\mu _{r}\mu _{0}SN^{2}}{l+\mu _{r}d}　　　　　&（リ）&　\frac {l}{\mu _{r}\mu _{0}S}+\frac {d}{\mu _{0}S} \\[ 5pt ] &（ヌ）&　0.5　　　　　&（ル）&　\frac {\mu _{r}\mu _{0}SN}{l+\mu _{r}d}　　　　　&（ヲ）&　\frac {\mu _{r}\mu _{0}S\sqrt {N}}{l+\mu _{r}d} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

空隙を含む磁気回路のインダクタンスを考える問題です。
(4)以降は全ての値を代入して計算してしまうと時間がかかるため，解答で紹介しているように求められた式から関係性を検討することをおすすめします。
電験$ \ 2 \ $種においても理論科目は時間管理が重要となる科目ですので，しっかりと工夫して解けるようになりましょう。

1.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $
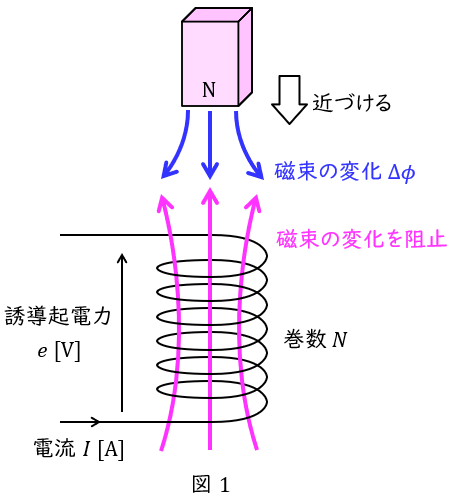
図1に示すように，巻数$ \ N \ $のコイルを貫通する磁束$ \ \phi \ \mathrm {[Wb]} \ $があるとき，コイルに発生する誘導起電力$ \ e \ \mathrm {[V]} \ $は，磁束の時間変化$ \ \displaystyle \frac {\Delta \phi }{\Delta t} \ $に比例し，
\[
\begin{eqnarray}
e&=&−N\frac {\Delta \phi }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] で求められます。これをファラデーの電磁誘導の法則といいます。一方，電流変化$ \ \Delta I \ \mathrm {[A]} \ $を考える場合，
\[
\begin{eqnarray}
e&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] という関係も成り立ち，$ \ L \ \mathrm {[H]}\ $を自己インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N\frac {\Delta \phi }{\Delta t}&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.磁気回路のオームの法則
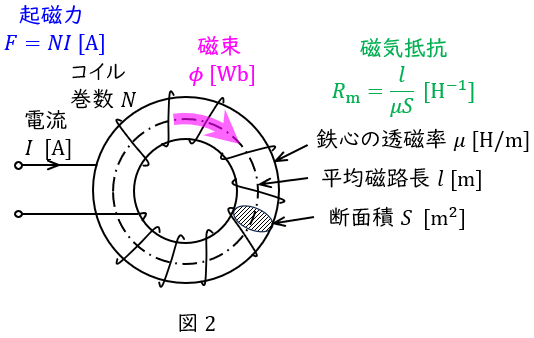
中心長さ$ \ l \ \mathrm {[ m ]} \ $の環状鉄心に巻数$ \ N \ $のコイルが巻かれ，そこに電流$ \ I \ \mathrm {[ A ]} \ $が流れている時，鉄心内の磁界の強さ$ \ H \ \mathrm {[ A / m ]} \ $は，アンペールの周回積分の法則より，
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ] H&=&\frac {NI}{l} \\[ 5pt ] \end{eqnarray}
\] であるから，鉄心内の磁束密度$ \ B \ \mathrm {[ T ]} \ $は，鉄心内の透磁率$ \ \mu \ \mathrm {[ H / m ]} \ $とすると，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] &=&\frac {\mu NI}{l} \\[ 5pt ] \end{eqnarray}
\] となります。鉄心内の磁束$ \ \phi \ \mathrm {[ Wb ]} \ $は，鉄心の断面積$ \ S \ \mathrm {[ m^{2} ]} \ $とすると，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ] \end{eqnarray}
\] となり，起磁力$ \ F=NI \ \mathrm {[ A ]} \ $，磁気抵抗$ \ R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S} \ \mathrm {[ H^{-1} ]} \ $とすると，
\[
\begin{eqnarray}
\phi &=&\frac {F}{R_{\mathrm {m}}} \\[ 5pt ] \end{eqnarray}
\] となり，磁気回路のオームの法則が成立します。また，このときの自己インダクタンス$ \ L \ \mathrm {[H]} \ $は，
\[
\begin{eqnarray}
L &=&\frac {N\phi }{I} \\[ 5pt ] &=&\frac {\displaystyle N\cdot \frac {NI}{R_{\mathrm {m}}}}{I} \\[ 5pt ] &=&\frac {N^{2}}{R_{\mathrm {m}}} \\[ 5pt ] &=&\frac {N^{2}}{\displaystyle \frac {l}{\mu S} } \\[ 5pt ] &=&\frac {\mu SN^{2}}{l} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：リ
各鉄心の磁路長が$ \ \displaystyle \frac {l}{2} \ $，空げき長が$ \ \displaystyle \frac {d}{2} \ $なので，磁気抵抗$ \ R_{\mathrm {m}} \ $は，ワンポイント解説「2.磁気回路のオームの法則」の磁気抵抗の公式より，
\[
\begin{eqnarray}
R_{\mathrm {m}} &=&\frac {\displaystyle \frac {l}{2}}{\mu _{r}\mu _{0}S}\times 2+\frac {\displaystyle \frac {d}{2}}{\mu _{0}S}\times 2 \\[ 5pt ] &=&\frac {l}{\mu _{r}\mu _{0}S}+\frac {d}{\mu _{0}S} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
自己インダクタンス$ \ L \ \mathrm {[H]} \ $は，ワンポイント解説「1.自己インダクタンスの定義$ \ L \ $」及び「2.磁気回路のオームの法則」の通り，
\[
\begin{eqnarray}
L &=&\frac {N\phi }{I} \\[ 5pt ] &=&\frac {\displaystyle N\cdot \frac {NI}{R_{\mathrm {m}}}}{I} \\[ 5pt ] &=&\frac {N^{2}}{R_{\mathrm {m}}} \\[ 5pt ] &=&\frac {N^{2}}{\displaystyle \frac {l}{\mu _{r}\mu _{0}S}+\frac {d}{\mu _{0}S}} \\[ 5pt ] &=&\frac {N^{2}}{\displaystyle \frac {l+\mu _{r}d}{\mu _{r}\mu _{0}S}} \\[ 5pt ] &=&\frac {\mu _{r}\mu _{0}SN^{2}}{l+\mu _{r}d} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
(2)解答式の通り，インダクタンスは巻き数の$ \ 2 \ $乗に比例するので，概略図は（ワ）のような形となる。

(4)解答：ホ
(2)解答式の通り，インダクタンスは巻き数$ \ N \ $の$ \ 2 \ $乗に比例するので，インダクタンスを$ \ 4 \ $倍とするためには巻き数を$ \ 2 \ $倍とすれば良い。

(5)解答：ヘ
(2)解答式について，空げき長$ \ d \ $は分母にある変数なので，インダクタンスを$ \ 4 \ $倍とするためには，分母の値を$ \ \displaystyle \frac {1}{4} \ $倍すれば良い。よって，変更後の空げき長を$ \ d^{\prime } \ $とすれば，
\[
\begin{eqnarray}
l+\mu _{r}d^{\prime } &=&\frac {1}{4}\left( l+\mu _{r}d\right) \\[ 5pt ] \end{eqnarray}
\] の関係が成立することから，$ \ d^{\prime } \ $について整理し各値を代入すると，
\[
\begin{eqnarray}
\mu _{r}d^{\prime } &=&\frac {1}{4}\left( l+\mu _{r}d\right) -l \\[ 5pt ] d^{\prime } &=&\frac {1}{4}\left( \frac {l}{\mu _{r}}+d\right) -\frac {l}{\mu _{r}} \\[ 5pt ] &=&\frac {1}{4}\times \left( \frac {250\times 10^{-3}}{2 \ 000}+0.8\times 10^{-3}\right) -\frac {250\times 10^{-3}}{2 \ 000} \\[ 5pt ] &≒&0.106 \ 3\times 10^{-3} \ \mathrm {[mm]} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \displaystyle \frac {d^{\prime }}{d} \ $は，
\[
\begin{eqnarray}
\frac {d^{\prime }}{d} &=&\frac {0.106 \ 3\times 10^{-3}}{0.8\times 10^{-3}} \\[ 5pt ] &≒&0.13 \\[ 5pt ] \end{eqnarray}
\] と求められる。