《理論》〈電磁気〉[H21:問1]静電界における電荷に働く力と発生する電界に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は、静電界に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式又は数値（最も近い数値）を解答群の中から選び，その記号をマークシートに記入しなさい。

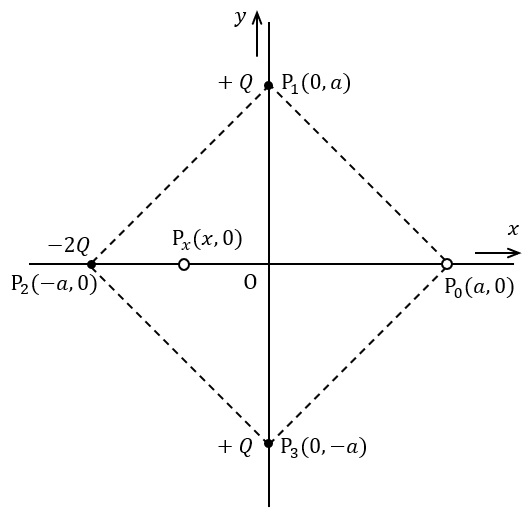
図のように，誘電率$ \ \varepsilon _{\mathrm {0}} \ $の真空中に$ \ 3 \ $個の点電荷が正方形の頂点にある。点$ \ \mathrm {P}_{\mathrm {1}} \ $と点$ \ \mathrm {P}_{\mathrm {3}} \ $には同じ値の正電荷$ \ +Q \ $（ただし，$ \ Q＞0 \ $及び$ \ a＞0 \ $）がそれぞれ置かれている。また，点$ \ \mathrm {P}_{\mathrm {2}} \ $には，負電荷$ \ -2Q \ $が置かれている。この静電界において，$ \ 2 \ $個の正電荷の間には反発力（斥力）$ \ \displaystyle \frac {Q^{2}}{4\pi \varepsilon _{\mathrm {0}}}\times \ \fbox {　（１）　} \ $が働いており，これら$ \ 2 \ $個の正電荷が点$ \ \mathrm {P}_{\mathrm {2}} \ $の負電荷に及ぼす合成力の大きさは，$ \ \displaystyle \frac {Q^{2}}{4\pi \varepsilon _{\mathrm {0}}}\times \ \fbox {　（２）　} \ $である。

次に，電界について検討しよう。まず，二つの正電荷による点$ \ \mathrm {P}_{\mathrm {0}} \ $での合成電界の$ \ y \ $軸成分は，$ \ \displaystyle \frac {Q}{4\pi \varepsilon _{\mathrm {0}}}\times \ \fbox {　（３）　} \ $である。また，$ \ 3 \ $個全部の電荷による合成電界の大きさは，点$ \ \mathrm {P}_{\mathrm {0}} \ $において，$ \ \displaystyle \frac {Q}{4\pi \varepsilon _{\mathrm {0}}}\times \ \fbox {　（４）　} \ $である。

いま，点$ \ \mathrm {P}_{\mathrm {2}} \ $の負電荷だけを$ \ x \ $軸に沿って正方向に動かして，
　　　　　点$ \ \mathrm {P}_{x} \ \left( \ \fbox {　（５）　} \ \times a , 0 \right) \ $
に置くと，点$ \ \mathrm {P}_{\mathrm {0}} \ $の合成電界を零にすることができる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　1　　　　　&（ロ）&　\frac {\sqrt {2}-1}{a^{2}}　　　　　&（ハ）&　\frac {\sqrt {2}-1}{2a^{2}} \\[ 5pt ] &（ニ）&　-0.68　　　　　&（ホ）&　\frac {1}{4a^{2}}　　　　　&（ヘ）&　-0.54 \\[ 5pt ] &（ト）&　0　　　　　&（チ）&　\frac {1}{\sqrt {2}a^{2}}　　　　　&（リ）&　\frac {\sqrt {2}+1}{2a^{2}} \\[ 5pt ] &（ヌ）&　\frac {\sqrt {2}}{a^{2}}　　　　　&（ル）&　\frac {1}{a}　　　　　&（ヲ）&　\frac {1}{2\sqrt {2}a^{2}} \\[ 5pt ] &（ワ）&　-0.44　　　　　&（カ）&　\frac {1}{a^{2}}　　　　　&（ヨ）&　\frac {1}{2a^{2}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

静電界における電荷の働きに関する問題です。
使う公式自体は難解なものはありませんが，(4)以降がやや計算量が多い問題です。$ \ 2 \ $種では$ \ 3 \ $種以上に高い計算力が求められますので，日頃からこのような問題を自力で解くクセをつけ，計算力を磨き上げるようにしましょう。

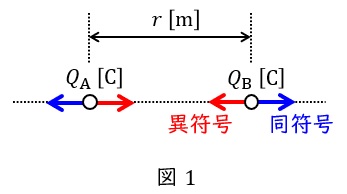
1.クーロンの法則
真空中で距離$ \ r \ \mathrm {[m]} \ $離れた二つの電荷$ \ Q_{\mathrm {A}} \ \mathrm {[C]} \ $，$ \ Q_{\mathrm {B}} \ \mathrm {[C]} \ $に加わる力$ \ F \ \mathrm {[N]} \ $は，真空の誘電率を$ \ \varepsilon _{0} \ \mathrm {[F / m]} \ $とすると，
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。このとき，$ \ Q_{\mathrm {A}} \ $，$ \ Q_{\mathrm {B}} \ $の$ \ + \ $$ \ – \ $の符号が同符号である場合には斥力（反発する力），異符号である場合には引力（引き合う力）が働きます。

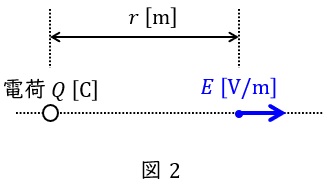
2.真空中の電界の大きさ
真空中に電荷$ \ Q \ \mathrm {[C]} \ $をおいた時，電荷から距離$ \ r \ \mathrm {[m]} \ $離れた場所の電界の大きさ$ \ E \ \mathrm {[N / C]} \ $は，真空の誘電率を$ \ \varepsilon _{0} \ \mathrm {[F / m]} \ $とすると，
\[
\begin{eqnarray}
E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。この場所に電荷$ \ q \ \mathrm {[C]} \ $の電荷を置けば，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] の力が働きます。

【解答】

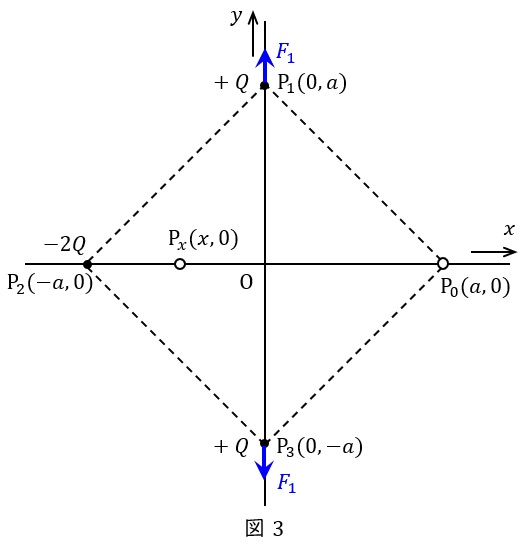
(1)解答：ホ
点$ \ \mathrm {P}_{\mathrm {1}} \ $と点$ \ \mathrm {P}_{\mathrm {3}} \ $の正電荷$ \ +Q \ $間には図3に示すような斥力が働き，$ \ 2 \ $点間の距離は$ \ 2a \ $なので，その大きさ$ \ F_{1} \ $は，ワンポイント解説「1.クーロンの法則」の通り，
\[
\begin{eqnarray}
F_{1} &=&\frac {Q\cdot Q}{4\pi \varepsilon _{0}\left( 2a\right) ^{2}} \\[ 5pt ] &=&\frac {Q^{2}}{4\pi \varepsilon _{0}\cdot 4a^{2}} \\[ 5pt ] &=&\frac {Q^{2}}{4\pi \varepsilon _{\mathrm {0}}}\times \frac {1}{4a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヌ
図4に示すように，点$ \ \mathrm {P}_{\mathrm {1}} \ $及び点$ \ \mathrm {P}_{\mathrm {3}} \ $の各正電荷$ \ +Q \ $と点$ \ \mathrm {P}_{\mathrm {2}} \ $の負電荷$ \ -2Q \ $間に働く力を$ \ {F_{\mathrm {2}}}^{\prime } \ $，求める合成力を$ \ F_{\mathrm {2}} \ $とする。$ \ {F_{\mathrm {2}}}^{\prime } \ $の大きさは，ワンポイント解説「1.クーロンの法則」の通り，電荷間の距離が$ \ \sqrt {2}a \ $なので，
\[
\begin{eqnarray}
{F_{\mathrm {2}}}^{\prime } &=&\frac {Q\cdot 2Q}{4\pi \varepsilon _{0}\left( \sqrt {2}a\right) ^{2}} \\[ 5pt ] &=&\frac {2Q^{2}}{4\pi \varepsilon _{0}\cdot 2a^{2}} \\[ 5pt ] &=&\frac {Q^{2}}{4\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] となり，求める合成力$ \ F_{\mathrm {2}} \ $は，
\[
\begin{eqnarray}
F_{\mathrm {2}} &=&\sqrt {2}{F_{\mathrm {2}}}^{\prime } \\[ 5pt ] &=&\frac {\sqrt {2}Q^{2}}{4\pi \varepsilon _{0}a^{2}} \\[ 5pt ] &=&\frac {Q^{2}}{4\pi \varepsilon _{\mathrm {0}}}\times \frac {\sqrt {2}}{a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

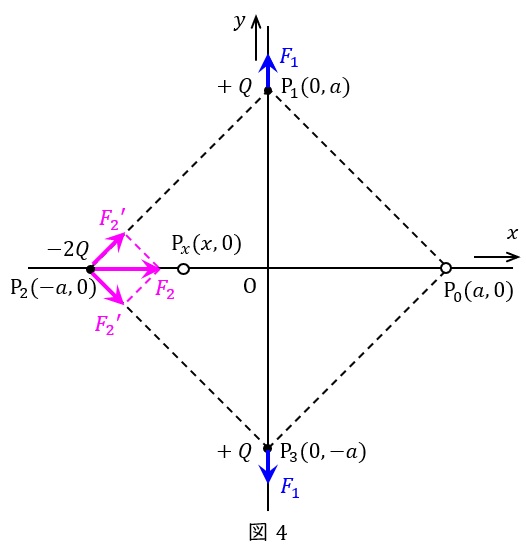
(3)解答：ト
各正電荷による点$ \ \mathrm {P}_{\mathrm {0}} \ $での電界を$ \ {E_{\mathrm {0}}}^{\prime } \ $，合成電界を$ \ E_{\mathrm {0}} \ $とすると，それぞれの電界は図5に示す通りとなる。
したがって，合成電界の$ \ y \ $軸成分は$ \ 0 \ $となる。

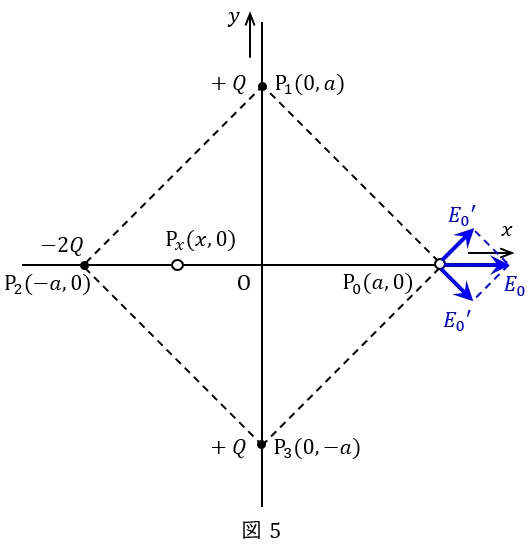
(4)解答：ハ
それぞれの電荷による点$ \ \mathrm {P}_{\mathrm {0}} \ $での電界を図6に示す。各正電荷による点$ \ \mathrm {P}_{\mathrm {0}} \ $での電界$ \ {E_{\mathrm {0}}}^{\prime } \ $の大きさは，ワンポイント解説「2.真空中の電界の大きさ」の通り，
\[
\begin{eqnarray}
{E_{\mathrm {0}}}^{\prime } &=&\frac {Q}{4\pi \varepsilon _{0}\left( \sqrt {2}a\right) ^{2}} \\[ 5pt ] &=&\frac {Q}{8\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，その合成電界$ \ E_{\mathrm {0}} \ $の大きさは，
\[
\begin{eqnarray}
E_{\mathrm {0}} &=&\sqrt {2}{E_{\mathrm {0}}}^{\prime } \\[ 5pt ] &=&\frac {\sqrt {2}Q}{8\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] となる。また，点$ \ \mathrm {P}_{\mathrm {2}} \ $の負電荷による点$ \ \mathrm {P}_{\mathrm {0}} \ $での電界$ \ E_{\mathrm {2}} \ $の大きさは，
\[
\begin{eqnarray}
E_{\mathrm {2}} &=&\frac {2Q}{4\pi \varepsilon _{0}\left( 2a\right) ^{2}} \\[ 5pt ] &=&\frac {Q}{8\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，全部の電界による電界$ \ E \ $の大きさは，
\[
\begin{eqnarray}
E &=&E_{\mathrm {0}}-E_{\mathrm {2}} \\[ 5pt ] &=&\frac {\sqrt {2}Q}{8\pi \varepsilon _{0}a^{2}}-\frac {Q}{8\pi \varepsilon _{0}a^{2}} \\[ 5pt ] &=&\frac {\left( \sqrt {2}-1\right) Q}{8\pi \varepsilon _{0}a^{2}} \\[ 5pt ] &=&\frac {Q^{2}}{4\pi \varepsilon _{\mathrm {0}}}\times \frac {\sqrt {2}-1}{2a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
点$ \ \mathrm {P}_{x} \ $に移動した負電荷による点$ \ \mathrm {P}_{\mathrm {0}} \ $での電界$ \ {E_{\mathrm {2}}}^{\prime } \ $の大きさは，
\[
\begin{eqnarray}
{E_{\mathrm {2}}}^{\prime } &=&\frac {2Q}{4\pi \varepsilon _{0}\left( a-x\right) ^{2}} \\[ 5pt ] &=&\frac {Q}{2\pi \varepsilon _{0}\left( a-x\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，点$ \ \mathrm {P}_{\mathrm {0}} \ $での合成電界が零とならなければならないので，
\[
\begin{eqnarray}
{E_{\mathrm {2}}}^{\prime } &=&E_{\mathrm {0}} \\[ 5pt ] \frac {Q}{2\pi \varepsilon _{0}\left( a-x\right) ^{2}}&=&\frac {\sqrt {2}Q}{8\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \frac {1}{\left( a-x\right) ^{2}}&=&\frac {\sqrt {2}}{4a^{2}} \\[ 5pt ] \sqrt {2}\left( a-x\right) ^{2}&=&4a^{2} \\[ 5pt ] \sqrt {\sqrt {2}}\left( a-x\right) &=&2a \\[ 5pt ] a-x&=&\frac {2a}{\sqrt {\sqrt {2}}} \\[ 5pt ] x&=&a-\frac {2a}{\sqrt {\sqrt {2}}} \\[ 5pt ] &≒&-0.68a \\[ 5pt ] \end{eqnarray}
\] と求められる。