《理論》〈電気回路〉[H21:問5]直流回路における電流源と電圧源の等価変換に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，電源を含む直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる数値を解答群の中から選び，その記号をマークシートに記入しなさい。

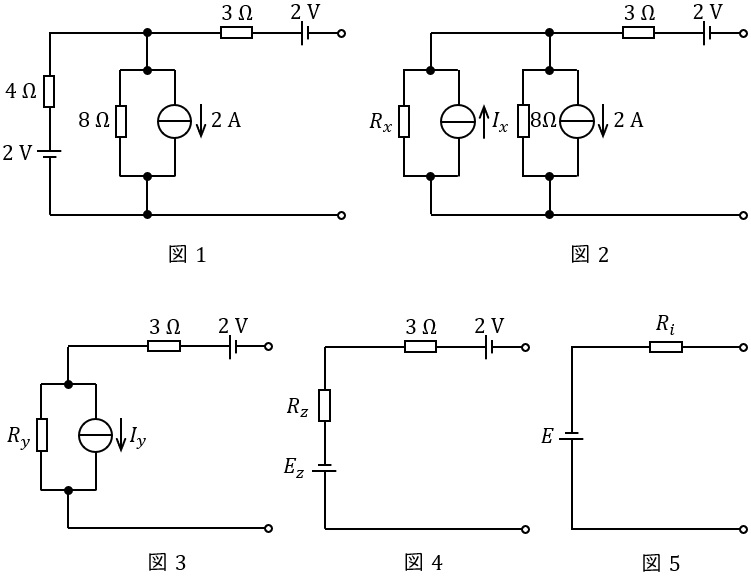
図1に示す電源を含む回路を図5の回路に等価変換したい。

まず，図1の$ \ 4 \ \mathrm {[\Omega ]} \ $の抵抗と$ \ 2 \ \mathrm {[V]} \ $の直流電圧源の直列接続部分を抵抗と電流源の並列接続となるように等価変換した回路を図2に示す。図2の$ \ R_{x} \ $と$ \ I_{x} \ $はそれぞれ$ \ R_{x}= \ \fbox {　（１）　} \ \mathrm {[\Omega ]} \ $と$ \ I_{x}= \ \fbox {　（２）　} \ \mathrm {[A]} \ $となる。

次に図2の回路を図3の形に書き直し，$ \ R_{y} \ $と$ \ I_{y} \ $を図4のように抵抗$ \ R_{z} \ $と電圧源$ \ E_{x} \ $の直列接続に再び等価変換したとき$ \ R_{z}= \ \fbox {　（３）　} \ \mathrm {[\Omega ]} \ $となる。さらに図4を図5の$ \ 1 \ $個の直流電圧源と$ \ 1 \ $個の抵抗の直列接続にまとめると$ \ R_{i}= \ \fbox {　（４）　} \ \mathrm {[\Omega ]} \ $で$ \ E= \ \fbox {　（５）　} \ \mathrm {[V]} \ $となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　1　　　　　&（ロ）&　2　　　　　&（ハ）&　4 \\[ 5pt ] &（ニ）&　\frac {8}{5}　　　　　&（ホ）&　\frac {20}{3}　　　　　&（ヘ）&　6 \\[ 5pt ] &（ト）&　\frac {4}{3}　　　　　&（チ）&　\frac {1}{2}　　　　　&（リ）&　\frac {25}{3} \\[ 5pt ] &（ヌ）&　\frac {17}{3}　　　　　&（ル）&　7　　　　　&（ヲ）&　5 \\[ 5pt ] &（ワ）&　\frac {8}{3}　　　　　&（カ）&　\frac {3}{2}　　　　　&（ヨ）&　8 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

直流回路における回路の等価変換に関する問題です。
本問では誘導されている形ですが，$ \ 2 \ $種合格を目指すならば図1から図5まで自力で変換できるぐらいになる必要があるかと思います。
直流回路は例年比較的取り組みやすい問題が出題されるので，ぜひ得点源にするようにして下さい。

1.電圧源と電流源の等価変換
図6に示すように，電圧源と電流源は抵抗との直列接続と並列接続で等価変換をすることができます。
電圧源の電圧$ \ E \ \mathrm {[V]} \ $と電流源の電流$ \ I \ \mathrm {[A]} \ $には，
\[
\begin{eqnarray}
E &=&rI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ハ
ワンポイント解説「1.電圧源と電流源の等価変換」の通り，電圧源と電流源を等価変換した場合でも抵抗値は同じなので，$ \ R_{x}=4 \ \mathrm {[\Omega ]} \ $と求められる。

(2)解答：チ
$ \ 2 \ \mathrm {[V]} \ $の電圧源と$ \ 4 \ \mathrm {[\Omega ]} \ $の抵抗を電流源に等価変換した電流値$ \ I_{x} \ \mathrm {[A]} \ $は，ワンポイント解説「1.電圧源と電流源の等価変換」の通り，
\[
\begin{eqnarray}
I_{x} &=&\frac {2}{4} \\[ 5pt ] &=&\frac {1}{2} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
$ \ R_{y} \ $は，$ \ R_{x}=4 \ \mathrm {[\Omega ]} \ $と$ \ 8 \ \mathrm {[\Omega ]} \ $の抵抗の並列合成抵抗なので，
\[
\begin{eqnarray}
R_{y} &=&\frac {R_{x}\times 8}{R_{x}+8} \\[ 5pt ] &=&\frac {4\times 8}{4+8} \\[ 5pt ] &=&\frac {8}{3} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，電流源を電圧源に置きかえても抵抗値は変わらないので，
\[
\begin{eqnarray}
R_{z} &=&R_{y} \\[ 5pt ] &=&\frac {8}{3} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヌ
$ \ R_{i} \ \mathrm {[\Omega ]} \ $は$ \ \displaystyle R_{z}=\frac {8}{3} \ \mathrm {[\Omega ]} \ $と$ \ 3 \ \mathrm {[\Omega ]} \ $の直列合成抵抗なので，
\[
\begin{eqnarray}
R_{i} &=&R_{z}+3 \\[ 5pt ] &=&\frac {8}{3}+3 \\[ 5pt ] &=&\frac {17}{3} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヘ
図3における$ \ I_{y} \ \mathrm {[A]} \ $は，$ \ \displaystyle I_{x}=\frac {1}{2} \ \mathrm {[A]} \ $と$ \ 2 \ \mathrm {[A]} \ $の電流源の合計なので，電流の向きに注意すると，
\[
\begin{eqnarray}
I_{y} &=&2-I_{x} \\[ 5pt ] &=&2-\frac {1}{2} \\[ 5pt ] &=&\frac {3}{2} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，図4における$ \ E_{z} \ \mathrm {[V]} \ $は，ワンポイント解説「1.電圧源と電流源の等価変換」の通り，
\[
\begin{eqnarray}
E_{z} &=&R_{y}I_{y} \\[ 5pt ] &=&\frac {8}{3}\times \frac {3}{2} \\[ 5pt ] &=&4 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，図5における$ \ E \ \mathrm {[V]} \ $は，$ \ E_{z}=4 \ \mathrm {[V]} \ $と$ \ 2 \ \mathrm {[V]} \ $の起電力の合計なので，
\[
\begin{eqnarray}
E_{z} &=&E_{z}+2 \\[ 5pt ] &=&4+2 \\[ 5pt ] &=&6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。