《理論》〈電気回路〉[H22:問6]直流ブリッジ回路に流れる電流に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，直流回路の電流に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる数値を解答群の中から選びなさい。

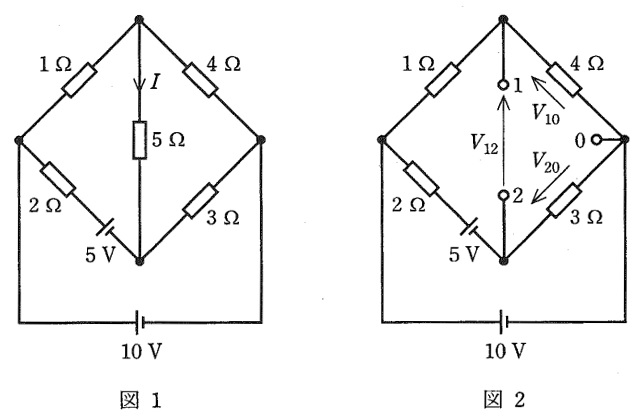
図1に示す直流回路において，$ \ 5 \ \mathrm {[\Omega ]} \ $の抵抗に流れる電流$ \ I \ $をテブナンの定理によって求めたい。

まず，$ \ 5 \ \mathrm {[\Omega ]} \ $の抵抗を取り除いた図2の回路において端子$ \ 1 – 2 \ $間に現れる電圧$ \ V_{12} \ $を求めると，$ \ V_{10} \ $が$ \ \fbox {　（１）　} \ \mathrm {[V]} \ $，$ \ V_{20} \ $が$ \ \fbox {　（２）　} \ \mathrm {[V]} \ $となることより，$ \ V_{12}= \ \fbox {　（３）　} \ \mathrm {[V]} \ $となる。ただし，$ \ V_{10} \ $及び$ \ V_{20} \ $はそれぞれ端子$ \ 0 \ $を基準とした端子$ \ 1 \ $の電圧及び端子$ \ 2 \ $の電圧である。

次に，図2の回路において回路内のすべての電圧源の電圧を零とした回路について端子$ \ 1 – 2 \ $間の抵抗を求めると$ \ \fbox {　（４）　} \ \mathrm {[\Omega ]} \ $となる。

以上より，端子$ \ 1 – 2 \ $間に$ \ 5 \ \mathrm {[\Omega ]} \ $の抵抗を接続したときに流れる電流$ \ I \ $はテブナンの定理により$ \ \fbox {　（５）　} \ \mathrm {[A]} \ $となる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　-\frac {2}{15}　　　　　&（ロ）&　9　　　　　&（ハ）&　5 \\[ 5pt ] &（ニ）&　7　　　　　&（ホ）&　10　　　　　&（ヘ）&　\frac {7}{6} \\[ 5pt ] &（ト）&　2　　　　　&（チ）&　1　　　　　&（リ）&　6 \\[ 5pt ] &（ヌ）&　8　　　　　&（ル）&　16　　　　　&（ヲ）&　3 \\[ 5pt ] &（ワ）&　-2　　　　　&（カ）&　4　　　　　&（ヨ）&　\frac {5}{7} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電源を２つ含むやや複雑な直流回路の回路計算に関する問題です。
こういう語群から解答が全く予測できない問題を高得点が取れるかどうかで合否が分かれます。
特に(1)～(3)は分圧の法則やキルヒホッフの法則を知っていれば解ける問題なので，確実に失点しないようにしましょう。

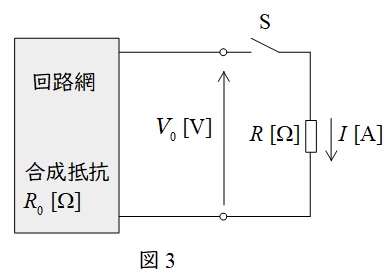
1.テブナンの定理
下図のような回路において，端子$ \ \mathrm {a-b} \ $の開放電圧を$ \ V_{\mathrm {0}} \ \mathrm {[V]} \ $，端子$ \ \mathrm {a-b} \ $から電源側をみた合成抵抗を$ \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ $とする（ただし，電圧源は短絡，電流源は開放する）と，図の抵抗$ \ R \ \mathrm {[\Omega ]} \ $を流れる電流の大きさ$ \ I \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)解答：ヌ
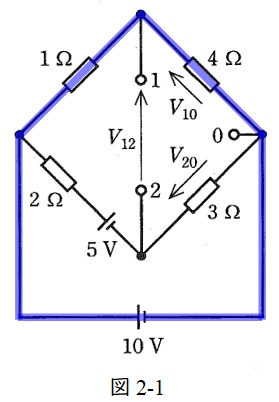
図2-1に示す閉回路に分圧の法則を適用すると，
\[
\begin{eqnarray}
V_{10}&=&\frac {4}{1+4}\times 10 \\[ 5pt ] &=&8 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヲ
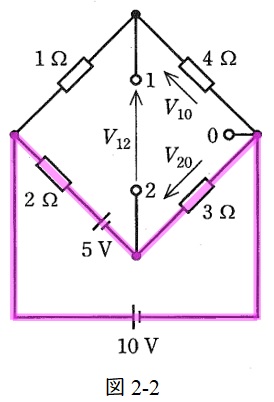
図2-2に示す閉回路にキルヒホッフの法則を適用すると，各抵抗に流れる電流$ \ I \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
10-5&=&2I+3I \\[ 5pt ] 5I&=&5 \\[ 5pt ] I&=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので$ \ V_{20} \ \mathrm {[V]} \ $は，オームの法則より，
\[
\begin{eqnarray}
V_{20}&=&3I \\[ 5pt ] &=&3\times 1 \\[ 5pt ] &=&3 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
(1)及び(2)より，$ \ V_{12} \ \mathrm {[V]} \ $は，
\[
\begin{eqnarray}
V_{12}&=&V_{10}-V_{20} \\[ 5pt ] &=&8-3 \\[ 5pt ] &=&5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ト
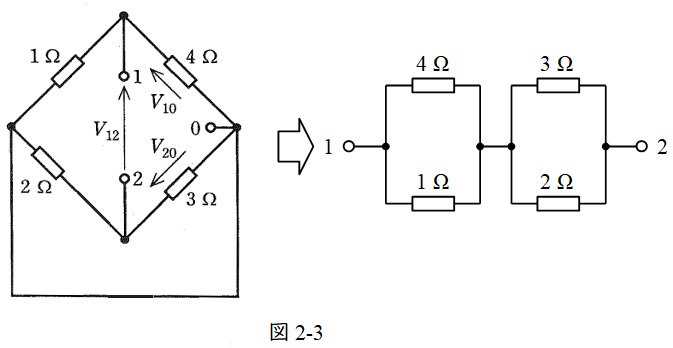
図2の各電圧源を短絡し，端子$ \ 1 – 2 \ $間から見た回路に整理すると図2-3の通りとなる。
よって，$ \ 1 – 2 \ $間から見た回路の合成抵抗$ \ R \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
R&=&\frac {4\times 1}{4+1}+\frac {3\times 2}{3+2} \\[ 5pt ] &=&\frac {4}{5}+\frac {6}{5} \\[ 5pt ] &=&2 \ \mathrm {[\Omega]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヨ
(3)及び(4)より，端子$ \ 1 – 2 \ $間に$ \ 5 \ \mathrm {[\Omega ]} \ $の抵抗を接続したときに流れる電流$ \ I \ $は，ワンポイント解説「1.テブナンの定理」の通り，
\[
\begin{eqnarray}
I&=&\frac {V_{12}}{R+5} \\[ 5pt ] &=&\frac {5}{2+5} \\[ 5pt ] &=&\frac {5}{7} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。