《理論》〈電気回路〉[H30:問5]直流回路の重ね合わせの理を用いた電流の導出に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，直流回路に関する記述である。文中の$\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}$に当てはまる最も適切なものを解答群の中から選べ。

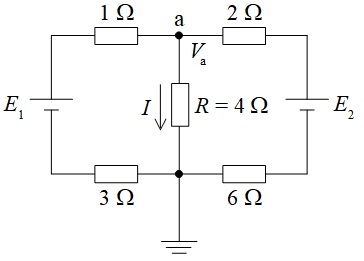
図のように電圧源$ \ E_{1} \ $，$ \ E_{2} \ $及び抵抗からなる直流回路において，重ね合わせの理を用いて抵抗$ \ R=4 \ \Omega \ $に流れる電流$ \ I \ $を求めたい。ただし，電流は矢印の向きを正とする。

まず，電圧源$ \ E_{1} \ $のみを考えたとき，抵抗$ \ R \ $を流れる電流$ \ I_{1} \ $は$\fbox {　（１）　}$となる。次に，電圧源$ \ E_{2} \ $のみを考えたとき，抵抗$ \ R \ $を流れる電流$ \ I_{2} \ $は$\fbox {　（２）　}$となる。

したがって，すべての電圧源について考えると，抵抗$ \ R \ $を流れる電流$ \ I \ $は，$ \ I=I_{1}+I_{2}=\fbox {　（３）　} \ $となる。また，図の点$ \ \mathrm {a} \ $の電位$ \ V_{\mathrm {a}} \ $は$\fbox {　（４）　}$となる。

ここで，$ \ E_{1} \ $，$ \ E_{2} \ $の関係が$ \ E_{2}=\fbox {　（５）　}$となる場合において電流$ \ I \ $は零となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {3E_{1}+E_{2}}{3}　　　&（ロ）&　-\frac {E_{1}}{2}　　　&（ハ）&　\frac {E_{2}}{10} \\[ 5pt ] &（ニ）&　\frac {E_{1}}{20}　　　&（ホ）&　\frac {E_{1}+2E_{2}}{5}　　　&（ヘ）&　\frac {E_{2}}{20} \\[ 5pt ] &（ト）&　\frac {E_{1}+2E_{2}}{20}　　　&（チ）&　-2E_{1}　　　　&（リ）&　\frac {3E_{1}+E_{2}}{12} \\[ 5pt ] &（ヌ）&　\frac {2E_{1}+E_{2}}{5}　　　&（ル）&　\frac {E_{2}}{12}　　　&（ヲ）&　\frac {E_{1}}{8} \\[ 5pt ] &（ワ）&　\frac {E_{1}}{10}　　　&（カ）&　\frac {2E_{1}+E_{2}}{20}　　　&（ヨ）&　-E_{1} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

導出過程も問題文中に記述があり，重ね合わせの理は三種でも非常に良く出題された問題であるため，二種受験者であればかなりの方が完答できたと思われる問題です。計算間違いに注意して確実に解くようにして下さい。

1.重ね合わせの理(重ねの理)
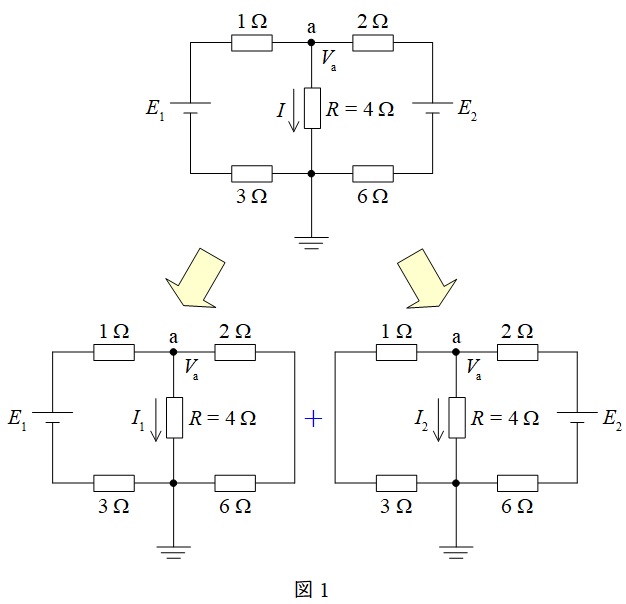
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。問題に対する回路は図1のようになります。

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

(1)解答：ワ
ワンポイント解説「1.重ね合わせの理(重ねの理)」より，電圧源$ \ E_{1} \ $のみを考えたとき，回路は図1左側のようになる。
回路の合成抵抗$ \ R_{1} \ $は，
\[
\begin{eqnarray}
R_{1} &=& 1+\frac {4\times (2+6)}{4+(2+6)}+3 \\[ 5pt ] &=& \frac {20}{3} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，電源を流れる電流$ \ I_{1}^{\prime } \ $は，
\[
\begin{eqnarray}
I_{1}^{\prime } &=& \frac {E_{1}}{R_{1}} \\[ 5pt ] &=& \frac {E_{1}}{\displaystyle \frac {20}{3}} \\[ 5pt ] &=& \frac {3}{20} E_{1} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，分流の法則より抵抗$ \ R \ $を流れる電流$ \ I_{1} \ $は，
\[
\begin{eqnarray}
I_{1}&=& \frac {2+6}{4+(2+6)}I_{1}^{\prime } \\[ 5pt ] &=& \frac {2}{3}\times \frac {3}{20} E_{1} \\[ 5pt ] &=& \frac { E_{1}}{10} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヘ
ワンポイント解説「1.重ね合わせの理(重ねの理)」より，電圧源$ \ E_{2} \ $のみを考えたとき，回路は図1右側のようになる。
回路の合成抵抗$ \ R_{2} \ $は，
\[
\begin{eqnarray}
R_{2} &=& 2+\frac {4\times (1+3)}{4+(1+3)}+6 \\[ 5pt ] &=& 10 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，電源を流れる電流$ \ I_{2}^{\prime } \ $は，
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {E_{2}}{R_{2}} \\[ 5pt ] &=& \frac {E_{2}}{10} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，分流の法則より抵抗$ \ R \ $を流れる電流$ \ I_{2} \ $は，
\[
\begin{eqnarray}
I_{2}&=& \frac {1+3}{4+(1+3)}I_{1}^{\prime } \\[ 5pt ] &=& \frac {1}{2}\times \frac {E_{2}}{10} \\[ 5pt ] &=& \frac { E_{2}}{20} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：カ
(1)，(2)より，
\[
\begin{eqnarray}
I&=&I_{1}+I_{2} \\[ 5pt ] &=& \frac { E_{1}}{10} +\frac { E_{2}}{20} \\[ 5pt ] &=& \frac { 2E_{1}+E_{2}}{20} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヌ
図の点$ \ \mathrm {a} \ $の電位$ \ V_{\mathrm {a}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {a}}&=&RI \\[ 5pt ] &=& 4\times \frac { 2E_{1}+E_{2}}{20} \\[ 5pt ] &=& \frac { 2E_{1}+E_{2}}{5} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：チ
(3)より，電流$ \ I \ $が零となるのは，
\[
\begin{eqnarray}
\frac { 2E_{1}+E_{2}}{20}&=&0 \\[ 5pt ] 2E_{1}+E_{2}&=&0 \\[ 5pt ] E_{2}&=& -2E_{1} \\[ 5pt ] \end{eqnarray}
\] となる。