《理論》〈電子理論〉[H22:問8]バイポーラトランジスタを用いた増幅回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

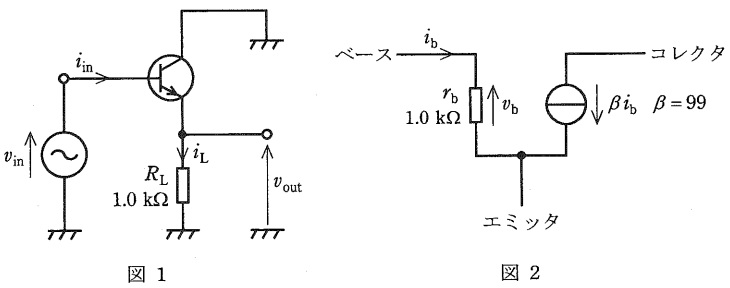
次の文章は， 図1に示すバイポーラトランジスタを用いた増幅回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる数値を解答群の中から選びなさい。ただし，図1は，増幅回路の交流成分のみを考慮しており，バイポーラトランジスタの交流等価回路は図2で表されるものとする。また，\( \ \beta \ \)はエミッタ接地電流増幅率であり，ベース電流の\( \ \beta \ \)倍がコレクタ電流となることを表している。

図1の電流\( \ i_{\mathrm {in}} \ \)はバイポーラトランジスタのベース電流\( \ i_{\mathrm {b}} \ \)に等しく，また，図2のバイポーラトランジスタの交流等価回路から\( \ \beta =99\ \)なので，抵抗\( \ R_{\mathrm {L}} \ \)に流れる電流\( \ i_{\mathrm {L}} \ \)は\( \ i_{\mathrm {in}} \ \)の\( \ \fbox {　 （１） 　} \ \)倍であることがわかる。このこととベース抵抗\( \ r_{\mathrm {b}} \ \)と抵抗\( \ R_{\mathrm {L}} \ \)が共に\( \ 1.0 \ \mathrm {[k\Omega ]} \ \)であることから，図1の増幅回路の入力抵抗は\( \ \displaystyle \frac {v_{\mathrm {in}}}{i_{\mathrm {in}}}= \ \fbox {　 （２） 　} \ \mathrm {[k\Omega ]} \ \)であることがわかる。同じく，\( \ i_{\mathrm {L}} \ \)は\( \ i_{\mathrm {in}} \ \)の\( \ \fbox {　 （１） 　} \ \)倍であることから，ベース抵抗\( \ r_{\mathrm {b}} \ \)に生じる電圧\( \ v_{\mathrm {b}} \ \)は抵抗\( \ R_{\mathrm {L}} \ \)に生じる電圧\( \ v_{\mathrm {out}} \ \)の\( \ \fbox {　 （３） 　} \ \)倍である。したがって，電圧利得\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は\( \ \fbox {　 （４） 　} \ \)倍となる。さらに，\( \ \beta \ \)を\( \ 99 \ \)よりも大きくしていくと，電圧利得\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は\( \ \fbox {　 （５） 　} \ \)倍に近づいていく。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　-101　　　　　&（ロ）&　101　　　　　&（ハ）&　\frac {1}{100} \\[ 5pt ] &（ニ）&　\frac {1}{99}　　　　　&（ホ）&　99　　　　　&（ヘ）&　-\frac {99}{100} \\[ 5pt ] &（ト）&　1　　　　　&（チ）&　0　　　　　&（リ）&　\frac {100}{101} \\[ 5pt ] &（ヌ）&　-1　　　　　&（ル）&　\frac {99}{101}　　　　&（ヲ）&　-100 \\[ 5pt ] &（ワ）&　100　　　　　&（カ）&　\frac {1}{101}　　　　&（ヲ）&　-99 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

バイポーラトランジスタを用いたコレクタ接地増幅回路に関する問題です。
キルヒホッフの法則以外には特別な公式は使用しませんので，マスターしてしまうと得点源になる問題です。
あまり勉強をしない受験生も多いので，狙い目の問題とも言えるかと思います。

【解答】

(1)解答：ワ
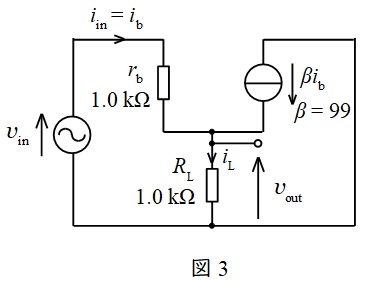
図1と図2を組み合わせた小信号等価回路は図3のようになる。
図3にキルヒホッフの法則（電流則）を適用すると，\( \ R_{\mathrm {L}} \ \)に流れる電流\( \ i_{\mathrm {L}} \ \)は，
\[
\begin{eqnarray}
i_{\mathrm {L}} &=&i_{\mathrm {b}}+\beta i_{\mathrm {b}} \\[ 5pt ] &=&\left( 1+\beta \right) i_{\mathrm {b}} \\[ 5pt ] &=&\left( 1+99 \right) i_{\mathrm {in}} \\[ 5pt ] &=&100 i_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

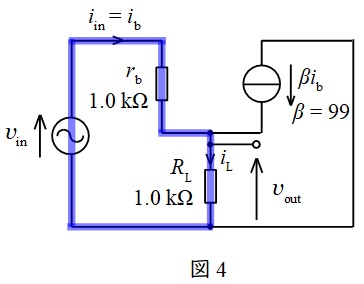
(2)解答：ロ
図4に示す閉回路にキルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
v_{\mathrm {in}} &=&r_{\mathrm {b}}i_{\mathrm {b}}+R_{\mathrm {L}} i_{\mathrm {L}} \\[ 5pt ] &=&1.0\times i_{\mathrm {in}}+1.0\times 100i_{\mathrm {in}} \\[ 5pt ] &=&101i_{\mathrm {in}} \\[ 5pt ] \frac {v_{\mathrm {in}}}{i_{\mathrm {in}}}&=&101 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
それぞれの抵抗についてオームの法則を適用すると，
\[
\begin{eqnarray}
\frac {v_{\mathrm {b}}}{v_{\mathrm {out}}} &=&\frac {r_{\mathrm {b}}i_{\mathrm {b}}}{R_{\mathrm {L}} i_{\mathrm {L}}} \\[ 5pt ] &=&\frac {1.0\times i_{\mathrm {b}}}{1.0\times 100 i_{\mathrm {b}}} \\[ 5pt ] &=&\frac {1}{100} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：リ
図4に示す閉回路について，各電圧の関係式より，
\[
\begin{eqnarray}
v_{\mathrm {in}} &=&v_{\mathrm {b}}+v_{\mathrm {out}} \\[ 5pt ] &=&\frac {1}{100}v_{\mathrm {out}}+v_{\mathrm {out}} \\[ 5pt ] &=&\frac {101}{100}v_{\mathrm {out}} \\[ 5pt ] \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {100}{101} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ト
\( \ \beta \ \)の値を大きくしていくと，\( \ r_{\mathrm {b}} \ \)に流れる電流は十分に小さく，電圧降下はほぼないと考えることができるので，\( \ v_{\mathrm {in}}≒v_{\mathrm {out}} \ \)と考えることができる。したがって，\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は\( \ 1 \ \)倍に近づいていく。