Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,\( \ 2 \ \)導体間及び大地に平行に張られた電線の静電容量に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句又は式を解答群の中から選びなさい。 ただし,空気の誘電率を\( \ \varepsilon _{0} \ \)とする。
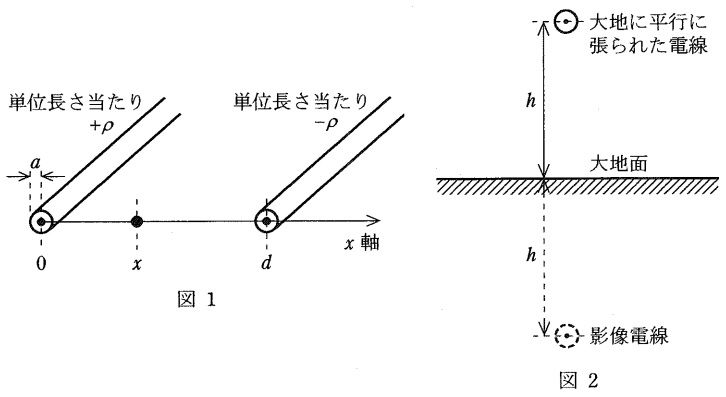
図1に示すように,空気中に半径\( \ a \ \), 導体間距離\( \ d \ \)の\( \ 2 \ \)本の無限長平行導体があり,各導体に単位長さ当たり\( \ +\rho \ \), \( \ -\rho \ \)の電荷を与えた場合を考える。ここで,\( \ d≫a \ \)とする。
このとき,\( \ 2 \ \)本の導体の軸を結ぶ平面上,単位長さ当たり\( \ +\rho \ \)の電荷を与えた導体の中心軸から\( \ x \ \)の点の電界の強さは,
\[
\begin{eqnarray}
E\left( x \right) &=& \ \fbox { (1) } \ \ ・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。
したがって,導体間の電位差は,
\[
\begin{eqnarray}
V &=&\int _{a}^{d-a} E\left( x \right) \mathrm {d}x= \ \fbox { (2) } \ ・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
と求まる。
よって,単位長さ当たりの導体間の静電容量は,
\[
\begin{eqnarray}
C &=& \ \fbox { (3) } \ \ ・・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
と計算できる。
次に,図2に示すように,平たんな大地面上の高さ\( \ h \ \)に大地と平行に張られた半径\( \ a \ \)の電線の大地に対する単位長さ当たりの静電容量を,影像法を用いて求める。ここで,\( \ h≫a \ \)とする。
まず,大地面上の高さ\( \ h \ \)の電線と平行に,大地中の深さ\( \ h \ \)に張られた半径\( \ a \ \)の影像電線を想定する。このとき,③式において\( \ d=2h \ \)を代入することで\( \ 2 \ \)電線間の単位長さ当たりの静電容量を求めることができる。この静電容量は,大地面と電線間の静電容量と,大地面と影像電線との間の仮想的な静電容量とが直列接続されたものである。したがって,電線の大地に対する単位長さ当たりの静電容量は,電線と影像電線とからなる\( \ 2 \ \)電線間の場合の\( \ \fbox { (4) } \ \)となる。 よって,電線の大地に対する単位長さ当たりの静電容量は,
\[
\begin{eqnarray}
C &=& \ \fbox { (5) } \ \ ・・・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
と求めることができる。なお,ここで,大地は完全導体であるとする。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 4 \ 倍 &(ロ)& \frac {\rho \varepsilon _{0}}{2\pi }\left[ \frac {1}{x^{2}}+\frac {1}{\left( d-x\right) ^{2}}\right] &(ハ)& \frac {\pi \varepsilon _{0}}{\displaystyle 2 \ln \frac {2h-a}{a}} \\[ 5pt ]
&(ニ)& \frac {\rho }{\pi \varepsilon _{0}}\left( \frac {1}{a}-\frac {1}{d-a}\right) &(ホ)& \frac {\pi \varepsilon _{0}}{\displaystyle \ln \frac {d-a}{a}} &(ヘ)& \frac {\rho ^{2}}{\pi \varepsilon _{0}}\ln \frac {h-a}{a} \\[ 5pt ]
&(ト)& \frac {\pi \varepsilon _{0}a\left( d-a\right) }{d-2a} &(チ)& \frac {\rho }{2\pi \varepsilon _{0}}\left[ \frac {1}{x^{2}}+\frac {1}{\left( d-x\right) ^{2}}\right] &(リ)& \frac {1}{2} \ 倍 \\[ 5pt ]
&(ヌ)& \frac {\rho }{2\pi \varepsilon _{0}}\left( \frac {1}{x}+\frac {1}{d-x}\right) &(ル)& \frac {\rho \varepsilon _{0}}{\pi }\left( \frac {1}{a}-\frac {1}{d-a}\right) &(ヲ)& \frac {\rho }{\pi \varepsilon _{0}}\ln \frac {d-a}{a} \\[ 5pt ]
&(ワ)& 2 \ 倍 &(カ)& \frac {\rho ^{2}}{\pi \varepsilon _{0}}\ln \frac {d-a}{a} &(ヨ)& \frac {2\pi \varepsilon _{0}}{\displaystyle \ln \frac {2h-a}{a}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電気影像法を利用した電線と大地間の静電容量を求める問題です。
(1)と(2)の計算量が多いため,ここで間違ってしまった人が大きく失点する問題であり,非常に点数差が拡がりやすい問題です。
電気影像法自体は一度理解してしまえばある程度パターン化されてくるので,過去問演習を繰り返してマスターするようにしましょう。
1.ガウスの定理
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの定理といいます。閉曲面が同軸円筒導体で,単位長さ当たりに蓄えられている電荷\( \ q \ \)があれば,単位長さ当たりの電界\( \ E \ \)は,
\[
\begin{eqnarray}
2\pi r \times 1 \cdot E &=& \frac {q}{\varepsilon } \\[ 5pt ]
E &=& \frac {q}{2\pi \varepsilon r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.空間上の電位\( \ V \ \)
中心からの距離\( \ r \ \mathrm {[m]} \ \)に関する電界\( \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ \)が与えられている時,その場所の電位\( \ V \ \mathrm {[V]} \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:ヌ
ワンポイント解説「1.ガウスの定理」の通り,\( \ +\rho \ \)の電荷による電界\( \ E_{1}\left( x \right) \ \)は,
\[
\begin{eqnarray}
E_{1}\left( x \right) &=& \frac {\rho }{2\pi \varepsilon _{0}x} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ -\rho \ \)の電荷による電界\( \ E_{2}\left( x \right) \ \)は,
\[
\begin{eqnarray}
E_{2}\left( x \right) &=& -\frac {\rho }{2\pi \varepsilon _{0}\left( d-x\right) } \\[ 5pt ]
\end{eqnarray}
\]
である。それぞれの電界の向きは共に右向きであることから,符号に注意すると,
\[
\begin{eqnarray}
E\left( x \right) &=& E_{1}\left( x \right) -E_{2}\left( x \right) \\[ 5pt ]
&=& \frac {\rho }{2\pi \varepsilon _{0}x}-\left\{ -\frac {\rho }{2\pi \varepsilon _{0}\left( d-x\right) }\right\} \\[ 5pt ]
&=& \frac {\rho }{2\pi \varepsilon _{0}x}+\frac {\rho }{2\pi \varepsilon _{0}\left( d-x\right) } \\[ 5pt ]
&=& \frac {\rho }{2\pi \varepsilon _{0}}\left( \frac {1}{x}+\frac {1}{d-x}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヲ
①式を②式に代入すると,
\[
\begin{eqnarray}
V &=&\int _{a}^{d-a} E\left( x \right) \mathrm {d}x \\[ 5pt ]
&=& \int _{a}^{d-a}\frac {\rho }{2\pi \varepsilon _{0}}\left( \frac {1}{x}+\frac {1}{d-x}\right) \mathrm {d}x \\[ 5pt ]
&=& \frac {\rho }{2\pi \varepsilon _{0}}\int _{a}^{d-a}\left( \frac {1}{x}+\frac {1}{d-x}\right) \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ A=d-x \ \)とすれば,\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}x}=-1 \ \)すなわち\( \ \displaystyle \mathrm {d}A=-\mathrm {d}x \ \)であり,\( \ x \ \)が\( \ a→d-a \ \)のとき\( \ A \ \)は \( \ d-a→a \ \)であるから,
\[
\begin{eqnarray}
V &=& \frac {\rho }{2\pi \varepsilon _{0}}\left\{ \int _{a}^{d-a}\frac {1}{x} \mathrm {d}x+\int _{d-a}^{a}\frac {1}{A} \left( -\mathrm {d}A\right) \right\} \\[ 5pt ]
&=& \frac {\rho }{2\pi \varepsilon _{0}}\left( \int _{a}^{d-a}\frac {1}{x} \mathrm {d}x-\int _{d-a}^{a}\frac {1}{A} \mathrm {d}A \right) \\[ 5pt ]
&=& \frac {\rho }{2\pi \varepsilon _{0}}\left( \left[ \ln x\right] _{a}^{d-a}-\left[ \ln A\right] _{d-a}^{a}\right) \\[ 5pt ]
&=& \frac {\rho }{2\pi \varepsilon _{0}}\left[ \left\{ \ln \left( d-a \right) -\ln a\right\} -\left\{ \ln a -\ln \left( d-a \right) \right\} \right] \\[ 5pt ]
&=& \frac {\rho }{\pi \varepsilon _{0}} \left\{ \ln \left( d-a \right) -\ln a\right\} \\[ 5pt ]
&=& \frac {\rho }{\pi \varepsilon _{0}}\ln \frac {d-a}{a} \\[ 5pt ] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
(2)の解答式を変形すると,
\[
\begin{eqnarray}
V &=& \frac {\rho }{\pi \varepsilon _{0}}\ln \frac {d-a}{a} \\[ 5pt ]
\frac {\rho }{V}&=& \frac {\pi \varepsilon _{0}}{\displaystyle \ln \frac {d-a}{a}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \rho =CV \ \)の関係から,
\[
\begin{eqnarray}
C&=& \frac {\pi \varepsilon _{0}}{\displaystyle \ln \frac {d-a}{a}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ワ
直列接続された場合のコンデンサの静電容量は\( \ \displaystyle \frac {1}{2} \ \)倍となるので,電線の大地に対する単位長さ当たりの静電容量は,電線と影像電線とからなる\( \ 2 \ \)電線間の場合の\( \ 2 \ \)倍となる。
(5)解答:ヨ
(3)の解答式に\( \ d=2h \ \)を代入して\( \ 2 \ \)倍すると,
\[
\begin{eqnarray}
C&=& \frac {2\pi \varepsilon _{0}}{\displaystyle \ln \frac {2h-a}{a}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは