Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,オシロスコープのプローブの等価回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
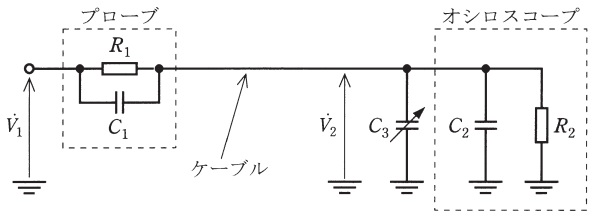
図において,\( \ {\dot V}_{1} \ \)はプローブ先端の被測定電圧,\( \ {\dot V}_{2} \ \)はオシロスコープの入力電圧,\( \ C_{1} \ \)及び\( \ R_{1} \ \)はプローブの静電容量及び抵抗,\( \ C_{2} \ \)及び\( \ R_{2} \ \)はオシロスコープの入力静電容量及び抵抗,\( \ C_{3} \ \)はプローブ補正用の可変静電容量であるとする。ただし,被測定電圧の角周波数は\( \ \omega \ \)(\( \ =2\pi f,f \ \)は周波数)であり,ケーブルの静電容量は無視できるものとする。
いま,簡単のために静電容量\( \ C_{1} \ \),\( \ C_{2} \ \)及び\( \ C_{3} \ \)を無視し,\( \ R_{2} \ \)を\( \ 1 \ \mathrm {[M\Omega ]} \ \),プローブの減衰率\( \ \displaystyle \frac {{\dot V}_{2}}{{\dot V}_{1}} \ \)を\( \ \displaystyle \frac {1}{10} \ \)とすれば,\( \ R_{1} \ \)は\( \ \fbox { (1) } \ \mathrm {[M\Omega ]} \ \)となる。
次に,\( \ C_{1} \ \),\( \ C_{2} \ \)及び\( \ C_{3} \ \)を考慮すれば,オシロスコープの入力電圧\( \ {\dot V}_{2} \ \)は\( \ \fbox { (2) }\times {\dot V}_{1} \ \)で表される。したがって,\( \ \left( C_{2}+C_{3}\right) R_{2}= \ \fbox { (3) } \ \)となるように\( \ C_{3} \ \)を調整すれば,\( \ \fbox { (2) } \ \)の\( \ \omega \ \)の項は消滅し,\( \ {\dot V}_{2} \ \)は\( \ \fbox { (4) }\times {\dot V}_{1} \ \)となる。この場合において,\( \ R_{2} \ \)を\( \ 1 \ \mathrm {[M\Omega ]} \ \),\( \ C_{1} \ \)を\( \ 10 \ \mathrm {[pF]} \ \),\( \ C_{2} \ \)を\( \ 20 \ \mathrm {[pF]} \ \),プローブの減衰率\( \ \displaystyle \frac {{\dot V}_{2}}{{\dot V}_{1}} \ \)を\( \ \displaystyle \frac {1}{10} \ \)とすれば,\( \ C_{3} \ \)は\( \ \fbox { (5) } \ \mathrm {[pF]} \ \)となる。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{2}}{R_{1}+R_{2}} &(ロ)& 10C_{1}R_{1} &(ハ)& \frac {R_{2}}{\displaystyle R_{2}+R_{1}\left[ \frac {1+\mathrm {j}\omega C_{1}R_{1}}{1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2} }\right] } \\[ 5pt ]
&(ニ)& 9 &(ホ)& \frac {R_{2}}{R_{1}} &(ヘ)& \frac {R_{1}}{\displaystyle R_{2}+R_{1}\left[ \frac {1+\mathrm {j}\omega C_{1}R_{1}}{1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2} }\right] } \\[ 5pt ]
&(ト)& 19 &(チ)& 170 &(リ)& 80 \\[ 5pt ]
&(ヌ)& C_{1}R_{1} &(ル)& 10 &(ヲ)& 70 \\[ 5pt ]
&(ワ)& \frac {R_{1}}{R_{1}+R_{2}} &(カ)& 2C_{1}R_{1} &(ヨ)& \frac {R_{2}}{\displaystyle R_{2}+R_{1}\left[ \frac {1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2} }{1+\mathrm {j}\omega C_{1}R_{1}}\right] } \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
コンデンサのリアクタンスや共振の条件等が分かれば解ける問題であり,特に3種の知識から発展した公式は使用せず解けます。電気・電子計測というよりも電気回路に近い問題と言えると思います。(2)及び(3)が本問の壁となりますので,確実に理解できるようにしておきましょう。
【解答】
(1)解答:ニ
\( \ C_{1} \ \),\( \ C_{2} \ \)及び\( \ C_{3} \ \)を無視すると,\( \ {\dot V}_{2} \ \)は分圧の法則より,
\[
\begin{eqnarray}
{\dot V}_{2}&=&\frac {R_{2}}{R_{1}+R_{2}}{\dot V}_{1} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\frac {{\dot V}_{2}}{{\dot V}_{1}}&=&\frac {R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\frac {1}{10}&=&\frac {1}{R_{1}+1} \\[ 5pt ]
R_{1}+1&=&10 \\[ 5pt ]
R_{1}&=&9 \ \mathrm {[M\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヨ
\( \ C_{1} \ \),\( \ C_{2} \ \)及び\( \ C_{3} \ \)を考慮したとき,\( \ C_{2} \ \),\( \ C_{3} \ \),\( \ R_{2} \ \)の合成アドミタンス\( \ {\dot Y}_{2} \ \)は,
\[
\begin{eqnarray}
{\dot Y}_{2}&=&\mathrm {j}\omega C_{2}+\mathrm {j}\omega C_{3}+\frac {1}{R_{2}} \\[ 5pt ]
&=&\frac {1}{R_{2}}+\mathrm {j}\omega \left( C_{2}+C_{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,合成インピーダンス\( \ {\dot Z}_{2} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{2}&=&\frac {1}{{\dot Y}_{2}} \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {1}{R_{2}}+\mathrm {j}\omega \left( C_{2}+C_{3}\right) } \\[ 5pt ]
&=&\frac {R_{2}}{1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,\( \ C_{1} \ \),\( \ R_{1} \ \)の合成インピーダンス\( \ {\dot Z}_{1} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{1}&=&\frac {\displaystyle R_{1}\cdot \frac {1}{\mathrm {j}\omega C}}{\displaystyle R_{1}+ \frac {1}{\mathrm {j}\omega C}} \\[ 5pt ]
&=&\frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,分圧の法則より\( \ {\dot V}_{2} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{2}&=&\frac {{\dot Z}_{2}}{{\dot Z}_{1}+{\dot Z}_{2}}{\dot V}_{1} \\[ 5pt ]
&=&\frac {\displaystyle \frac {R_{2}}{1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2}}}{\displaystyle \frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}}+\frac {R_{2}}{1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2}}}{\dot V}_{1} \\[ 5pt ]
&=&\frac {R_{2}}{\displaystyle \frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}}\cdot \left\{ 1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2}\right\}+R_{2}}{\dot V}_{1} \\[ 5pt ]
&=&\frac {R_{2}}{\displaystyle R_{2}+R_{1}\left[ \frac {1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2} }{1+\mathrm {j}\omega C_{1}R_{1}}\right] }{\dot V}_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヌ
(2)解答式の\( \ \omega \ \)の影響をなくすためには,分母の\( \ \omega \ \)を含む項が\( \ \omega \ \)の値を問わず一定であれば良い。したがって,
\[
\begin{eqnarray}
\frac {1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2} }{1+\mathrm {j}\omega C_{1}R_{1}}&=&K(定数) \\[ 5pt ]
\end{eqnarray}
\]
と置くと,
\[
\begin{eqnarray}
1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2}&=&K\left( 1+\mathrm {j}\omega C_{1}R_{1}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,実数項が等しい条件より\( \ K=1 \ \)となり,虚数項が等しい条件より,
\[
\begin{eqnarray}
\omega \left( C_{2}+C_{3}\right) R_{2}&=&\omega C_{1}R_{1} \\[ 5pt ]
\left( C_{2}+C_{3}\right) R_{2}&=&C_{1}R_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:イ
(3)の条件が成立するとき,(2)の解答式は,
\[
\begin{eqnarray}
{\dot V}_{2}&=&\frac {R_{2}}{\displaystyle R_{2}+R_{1}\left[ \frac {1+\mathrm {j}\omega \left( C_{2}+C_{3}\right) R_{2} }{1+\mathrm {j}\omega C_{1}R_{1}}\right] }{\dot V}_{1} \\[ 5pt ]
&=&\frac {R_{2}}{\displaystyle R_{2}+R_{1}\left( \frac {1+\mathrm {j}\omega C_{1}R_{1} }{1+\mathrm {j}\omega C_{1}R_{1}}\right) }{\dot V}_{1} \\[ 5pt ]
&=&\frac {R_{2}}{\displaystyle R_{1}+R_{2} }{\dot V}_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
(1)の解答より\( \ R_{1} =9 \ \mathrm {[M\Omega ]} \ \)であることに注意して(3)の解答式に各値を代入すると,
\[
\begin{eqnarray}
\left( 20\times 10^{-12}+C_{3}\right) \times 1\times 10^{6}&=&10\times 10^{-12}\times 9\times 10^{6} \\[ 5pt ]
20\times 10^{-12}+C_{3}&=&10\times 10^{-12}\times 9 \\[ 5pt ]
C_{3}&=&70\times 10^{-12} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ C_{3} \ \)は\( \ 70 \ \mathrm {[pF]} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは