《理論》〈電気回路〉[H25:問5]重ね合わせの理を利用した直流回路計算に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，電圧源と抵抗とからなる直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

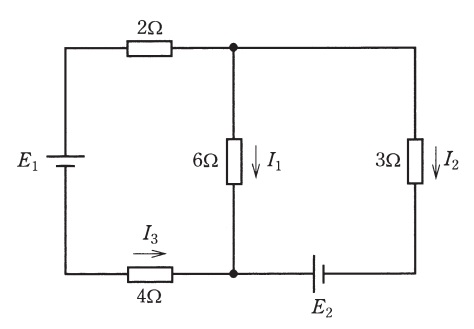
図のように電圧源と抵抗を接続した回路があり，重ね合わせの理を用いて抵抗に流れる電流$ \ I_{1} \ $，$ \ I_{2} \ $，$ \ I_{3} \ $を求めたい。$ \ E_{1}=8 \ \mathrm {[V]} \ $，$ \ E_{2}=9 \ \mathrm {[V]} \ $とする。電流は矢印の向きを正とする。

電圧源$ \ E_{1} \ $のみについて考えたとき，電流$ \ I_{1} \ $は$ \ \fbox {　（１）　} \ \mathrm {[A]} \ $，電流$ \ I_{2} \ $は$ \ \fbox {　（２）　} \ \mathrm {[A]} \ $となる。電圧源$ \ E_{2} \ $のみについて考えたとき，電流$ \ I_{1} \ $は$ \ \fbox {　（３）　} \ \mathrm {[A]} \ $，電流$ \ I_{2} \ $は$ \ \fbox {　（４）　} \ \mathrm {[A]} \ $となる。

よってすべての電圧源について考えると，
\[
\begin{eqnarray}
I_{1} &=& \ \fbox {　（１）　} \ + \ \fbox {　（３）　} \ \mathrm {[A]} \ \\[ 5pt ] I_{2} &=& \ \fbox {　（２）　} \ + \ \fbox {　（４）　} \ \mathrm {[A]} \ \\[ 5pt ] I_{3} &=& \ \fbox {　（５）　} \ \mathrm {[A]} \ \\[ 5pt ] \end{eqnarray}
\] である。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　-\frac {7}{4}　　　　　&（ロ）&　-\frac {3}{2}　　　　　&（ハ）&　-\frac {4}{3}\\[ 5pt ] &（ニ）&　-1　　　&（ホ）&　-\frac {3}{4}　　　&（ヘ）&　-\frac {1}{2} \\[ 5pt ] &（ト）&　0　　　&（チ）&　\frac {1}{3}　　　&（リ）&　\frac {2}{3} \\[ 5pt ] &（ヌ）&　\frac {3}{4}　　　&（ル）&　1　　　&（ヲ）&　\frac {4}{3} \\[ 5pt ] &（ワ）&　\frac {3}{2}　　　&（カ）&　\frac {8}{3} 　　　&（ヨ）&　3 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

三種から非常によく出題されている重ね合わせの理に関する問題です。電験二種合格を目指す上では確実に完答したい問題と言えるでしょう。

1.重ね合わせの理
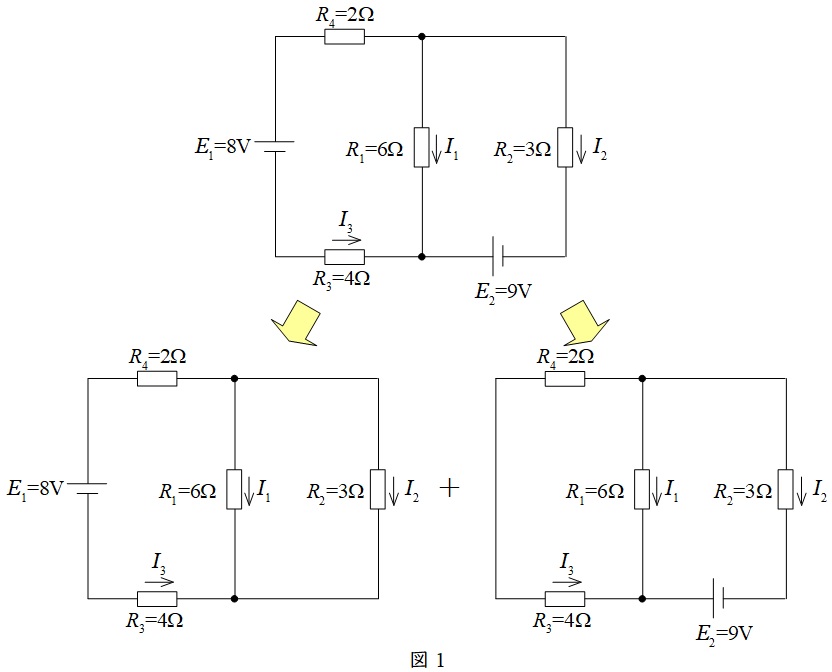
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。問題に対する回路は図1のようになります。

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

(1)解答：チ
(2)解答：リ
各抵抗を図1のようにおく。電圧源$ \ E_{1} \ $のみについて考えたときの合成抵抗$ \ R \ $は，
\[
\begin{eqnarray}
R &=&R_{4}+\frac {R_{1}R_{2}}{R_{1}+R_{2}}+R_{3} \\[ 5pt ] &=&2+\frac {6\times 3}{6+3}+4 \\[ 5pt ] &=&8 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，$ \ R_{3} \ $を流れる電流$ \ I_{31} \ $は，
\[
\begin{eqnarray}
I_{31} &=&-\frac {E_{1}}{R} \\[ 5pt ] &=&-\frac {8}{8} \\[ 5pt ] &=&-1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，分流の法則により，$ \ R_{1} \ $を流れる電流$ \ I_{11} \ $及び$ \ R_{2} \ $を流れる電流$ \ I_{21} \ $は，
\[
\begin{eqnarray}
I_{11} &=&\frac {R_{2}}{R_{1}+R_{2}} \times \left( -I_{31}\right) \\[ 5pt ] &=&\frac {3}{6+3} \times 1 \\[ 5pt ] &=&\frac {1}{3} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
I_{21} &=&\frac {R_{1}}{R_{1}+R_{2}} \times \left( -I_{31}\right) \\[ 5pt ] &=&\frac {6}{6+3} \times 1 \\[ 5pt ] &=&\frac {2}{3} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
(4)解答：ワ
各抵抗を図1のようにおく。電圧源$ \ E_{2} \ $のみについて考えたときの合成抵抗$ \ R^{\prime } \ $は，
\[
\begin{eqnarray}
R^{\prime } &=&\frac {R_{1}\left( R_{3}+R_{4}\right) }{R_{1}+\left( R_{3}+R_{4}\right) }+R_{2} \\[ 5pt ] &=&\frac {6\times \left( 4+2\right) }{6+\left( 4+2\right) }+3 \\[ 5pt ] &=&6 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，$ \ R_{2} \ $を流れる電流$ \ I_{22} \ $は，
\[
\begin{eqnarray}
I_{22} &=&\frac {E_{2}}{R^{\prime }} \\[ 5pt ] &=&\frac {9}{6} \\[ 5pt ] &=&\frac {3}{2} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，分流の法則により，$ \ R_{1} \ $を流れる電流$ \ I_{12} \ $及び$ \ R_{3} \ $を流れる電流$ \ I_{32} \ $は，
\[
\begin{eqnarray}
I_{12} &=&-\frac {R_{3}+R_{4}}{R_{1}+\left( R_{3}+R_{4}\right) } \times I_{22} \\[ 5pt ] &=&-\frac {4+2}{6+\left( 4+2\right) } \times \frac {3}{2} \\[ 5pt ] &=&-\frac {3}{4} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
I_{32} &=&-\frac {R_{1}}{R_{1}+\left( R_{3}+R_{4}\right) } \times I_{22} \\[ 5pt ] &=&-\frac {6}{6+\left( 4+2\right) } \times \frac {3}{2} \\[ 5pt ] &=&-\frac {3}{4} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：イ
重ね合わせの理より，$ \ R_{3} \ $を流れる電流$ \ I_{3} \ $は，
\[
\begin{eqnarray}
I_{3} &=&I_{31}+I_{32} \\[ 5pt ] &=&-1-\frac {3}{4} \\[ 5pt ] &=&-\frac {7}{4} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。