《理論》〈電気回路〉[H26:問4]RLC回路の過渡現象に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】
- 3.1 【本問に関する質疑応答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，回路の過渡現象に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

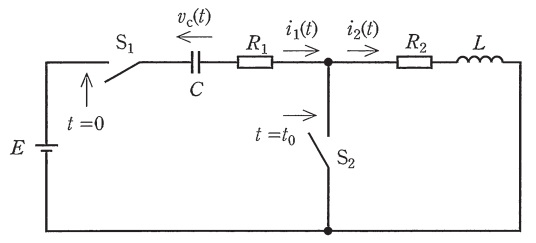
図のように直流電圧源$ \ E \ $に接続された$ \ RLC \ $回路を考える。ただし，時刻$ \ t＜0 \ $ではスイッチ$ \ \mathrm {S}_{1} \ $と$ \ \mathrm {S}_{2} \ $は開いており，コンデンサの電荷は零とする。

時刻$ \ t=0 \ $でスイッチ$ \ \mathrm {S}_{1} \ $を閉じ，次に回路が定常状態になる前の時刻$ \ t=t_{0} \ $ ( $＞0$ )でスイッチ$ \ \mathrm {S}_{2} \ $を閉じた。$ \ t≧t_{0} \ $では回路は左右の二つの独立な回路に分けて考えることができる。$ \ v_{\mathrm {c}} ( t_{0} ) \ $と$ \ i_{2} ( t_{0} ) \ $を使うと$ \ t≧t_{0} \ $における抵抗$ \ R_{1} \ $の電流$ \ i_{1} ( t ) \ $と抵抗$ \ R_{2} \ $の電流$ \ i_{2} ( t ) \ $は
\[
\begin{eqnarray}
i_{1} ( t ) &=&\fbox {　（１）　} \ \mathrm {e}^{-\fbox {　（２）　} ( t-t_{0} ) }　　&\cdots \cdots \cdots \cdots \cdots　①& \\[ 5pt ] i_{2} ( t ) &=&i_{2} ( t_{0} ) \mathrm {e}^{-\fbox {　（３）　} ( t-t_{0} ) }　　&\cdots \cdots \cdots \cdots \cdots　②& \\[ 5pt ] \end{eqnarray}
\] と表すことができる。ここで，スイッチ$ \ \mathrm {S}_{2} \ $が開いている間は$ \ i_{1} ( t ) =i_{2} ( t ) \ $であるが，$ \ t=t_{0} \ $でスイッチ$ \ \mathrm {S}_{2} \ $が閉じたときは$ \ i_{1} ( t_{0} ) =i_{2} ( t_{0} ) \ $であるとは限らない。ただし，$ \ v_{\mathrm {c}} ( t_{0} ) \ $と$ \ i_{2} ( t_{0} ) \ $が等式$ \ \fbox {　（４）　} \ $を満たすときは，$①$式と$②$式より$ \ i_{1} ( t_{0} ) =i_{2} ( t_{0} ) \ $となる。また，$ \ v_{\mathrm {c}} ( t_{0} ) \ $が等式$ \ \fbox {　（５）　} \ $を満たすときは，$ \ t=t_{0} \ $でスイッチ$ \ \mathrm {S}_{2} \ $を閉じると電流$ \ i_{1} ( t ) \ $は$ \ t≧t_{0} \ $で零(一定)となる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　v_{\mathrm {c}} ( t_{0} ) =0　　　&（ロ）&　\frac {v_{\mathrm {c}} ( t_{0} )}{R_{1}}=i_{2} ( t_{0} ) 　　　&（ハ）&　\frac {v_{\mathrm {c}} ( t_{0} )}{R_{1}} \\[ 5pt ] &（ニ）&　\frac {E+v_{\mathrm {c}} ( t_{0} )}{R_{1}}=i_{2} ( t_{0} )　　　&（ホ）&　\frac {E+v_{\mathrm {c}} ( t_{0} )}{R_{1}}　　　&（ヘ）&　\frac {E-v_{\mathrm {c}} ( t_{0} )}{R_{1}} \\[ 5pt ] &（ト）&　\frac {1}{R_{2}L}　　　&（チ）&　\frac {R_{1}}{C}　　　　&（リ）&　\frac {C}{R_{1}} \\[ 5pt ] &（ヌ）&　\frac {L}{R_{2}}　　　&（ル）&　\frac {E-v_{\mathrm {c}} ( t_{0} )}{R_{1}}=i_{2} ( t_{0} )　　　&（ヲ）&　\frac {R_{2}}{L} \\[ 5pt ] &（ワ）&　v_{\mathrm {c}} ( t_{0} ) =-E　　　&（カ）&　\frac {1}{CR_{1}}　　　&（ヨ）&　v_{\mathrm {c}} ( t_{0} ) =E \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

過渡現象に関する問題は解法がパターン化されており，毎年のように出題されるので，確実に得点できるようにしておきたいところです。本問は(1)，(2)がやや複雑で正答率も低めであると思うので，得点差が大きく開くと考えられます。

1.過渡現象における$ \ RLC \ $それぞれの電圧
線路に流れる電流を$ \ i \ $とし，抵抗$ \ R \ $の電圧$ \ V_{\mathrm{R}} \ $，リアクトル$ \ L \ $の電圧$ \ V_{\mathrm{L}} \ $，コンデンサ$ \ C \ $の電圧$ \ V_{\mathrm{C}} \ $とすると，
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，電荷$ \ q \ $との間に$ \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ $の関係があるので，
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& R\frac {\mathrm {d}q}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {q}{C}
\end{eqnarray}
\] となります。

2.過渡現象における定常解と過渡解
ⅰ．定常解を$ \ i_{\mathrm {s}} \ $，過渡解を$ \ i_{\mathrm {t}} \ $とすると，電流値$ \ i \ $は$ \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ $となります。
ⅱ．定常解は電流の時間変化のない状態すなわち$ \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ $とした時の解です。
ⅲ．過渡解はスイッチを入れた直後の解すなわち$ \ L \ $開放($ \ E=0 \ $と同義)の時の解です。

3.自然対数の微分積分
①自然対数の微分
\[
\frac {\mathrm {d}}{\mathrm {d}x} \ln {x} =\frac {1}{x}　
\] ②自然対数の積分
\[
\int \frac {1}{x} \mathrm {d}x =\ln {x} + C \left( Cは積分定数\right)
\] \[
\ln {x}=-\alpha t +C \left( Cは積分定数\right)の時，　x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。
\]

【解答】

(1)解答：ヘ
(2)解答：カ
問題図の左側の回路について回路方程式を立てると，
\[
\begin{eqnarray}
R_{1}i_{1} ( t ) +\frac {1}{C}\int i_{1} \mathrm {d}t &=&E \\[ 5pt ] \end{eqnarray}
\] であり，$\displaystyle i_{1} ( t ) =\frac {\mathrm {d}q_{1}}{\mathrm {d}t}$の関係があるから，
\[
\begin{eqnarray}
R_{1}\frac {\mathrm {d}q_{1}}{\mathrm {d}t} +\frac {q_{1} ( t ) }{C} &=&E \\[ 5pt ] \end{eqnarray}
\] となる。まず，定常解$ \ q_{\mathrm {1s}} ( t ) \ $を求めると，$ \ \displaystyle \frac {\mathrm {d}q_{\mathrm {1s}}}{\mathrm {d}t}=0 \ $であるから，
\[
\begin{eqnarray}
\frac {q_{\mathrm {1s}} ( t ) }{C} &=&E \\[ 5pt ] q_{\mathrm {1s}} ( t ) &=&CE \\[ 5pt ] \end{eqnarray}
\] と求められる。次に，過渡解$ \ q_{\mathrm {1t}} ( t ) \ $を求めると，
\[
\begin{eqnarray}
R_{1}\frac {\mathrm {d}q_{\mathrm {1t}}}{\mathrm {d}t} +\frac {q_{\mathrm {1t}} ( t ) }{C} &=&0 \\[ 5pt ] R_{1}\frac {\mathrm {d}q_{\mathrm {1t}}}{\mathrm {d}t} &=&-\frac {q_{\mathrm {1t}} ( t ) }{C} \\[ 5pt ] \frac {1}{q_{\mathrm {1t}} ( t ) }\mathrm {d}q_{\mathrm {1t}} &=&-\frac {1}{CR_{1}}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] 両辺積分すると，
\[
\begin{eqnarray}
\ln \left( q_{\mathrm {1t}} ( t ) \right) &=&-\frac {1}{CR_{1}} t +C (Cは積分定数) \\[ 5pt ] q_{\mathrm {1t}} ( t ) &=&A\mathrm {e}^{-\frac {1}{CR_{1}} t } (A=\mathrm {e}^{C}は積分定数) \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，一般解$ \ q_{1} ( t ) \ $は，
\[
\begin{eqnarray}
q_{1} ( t ) &=&q_{\mathrm {1s}} ( t ) + q_{\mathrm {1t}} ( t ) \\[ 5pt ] &=&CE+A\mathrm {e}^{-\frac {1}{CR_{1}} t } \\[ 5pt ] \end{eqnarray}
\] と求められる。題意より$ \ q_{\mathrm {1}} ( t_{0} ) =Cv_{\mathrm {C}} ( t_{0} ) \ $であるから，
\[
\begin{eqnarray}
Cv_{\mathrm {C}} ( t_{0} ) &=&CE+A\mathrm {e}^{-\frac {1}{CR_{1}} t_{0} } \\[ 5pt ] A\mathrm {e}^{-\frac {1}{CR_{1}} t_{0} } &=&Cv_{\mathrm {C}} ( t_{0} ) -CE \\[ 5pt ] A &=&C \left\{ v_{\mathrm {C}} ( t_{0} ) -E \right\} \mathrm {e}^{\frac {1}{CR_{1}} t_{0} } \\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
q_{\mathrm {1}} ( t ) &=&CE+C \left\{ v_{\mathrm {C}} ( t_{0} ) -E \right\} \mathrm {e}^{\frac {1}{CR_{1}} t_{0} }\cdot \mathrm {e}^{-\frac {1}{CR_{1}} t } \\[ 5pt ] &=&CE+C \left\{ v_{\mathrm {C}} ( t_{0} ) -E \right\} \mathrm {e}^{-\frac {1}{CR_{1}} ( t – t_{0} ) } \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，電流$ \ i_{1} ( t ) \ $は，
\[
\begin{eqnarray}
i_{\mathrm {1}} ( t ) &=&\frac {\mathrm {d}q_{1}}{\mathrm {d}t} \\[ 5pt ] &=&\frac {\mathrm {d}}{\mathrm {d}t}\left[ CE+C \left\{ v_{\mathrm {C}} ( t_{0} ) -E \right\} \mathrm {e}^{-\frac {1}{CR_{1}} ( t – t_{0} ) }\right] \\[ 5pt ] &=&C \left\{ v_{\mathrm {C}} ( t_{0} ) -E \right\} \cdot \left( -\frac {1}{CR_{1}}\right) \cdot \mathrm {e}^{-\frac {1}{CR_{1}} ( t – t_{0} ) } \\[ 5pt ] &=&\frac {E-v_{\mathrm {C}} ( t_{0} ) }{R_{1}} \mathrm {e}^{-\frac {1}{CR_{1}} ( t – t_{0} ) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
問題図の右側の回路について回路方程式を立てると，
\[
\begin{eqnarray}
R_{2}i_{2} ( t ) +L\frac {\mathrm {d}i_{2}}{\mathrm {d}t} &=&0 \\[ 5pt ] \end{eqnarray}
\] となるので，変数分離により一般解を求めると，
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{2}}{\mathrm {d}t} &=&-R_{2}i_{2} ( t ) \\[ 5pt ] \frac {1}{i_{2} ( t ) }\mathrm {d}i_{2} &=&-\frac {R_{2}}{L}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] 両辺積分すると，
\[
\begin{eqnarray}
\ln i_{2} ( t ) &=&-\frac {R_{2}}{L}t +C (Cは積分定数) \\[ 5pt ] i_{2} ( t ) &=&A\mathrm {e}^{-\frac {R_{2}}{L}t} (A=\mathrm {e}^{C}は積分定数) \\[ 5pt ] \end{eqnarray}
\] と求められる。題意より，$ \ i_{2} ( t_{0} ) \ $が与えられているので，
\[
\begin{eqnarray}
i_{2} ( t_{0} ) &=&A\mathrm {e}^{-\frac {R_{2}}{L}t_{0}} \\[ 5pt ] A &=&i_{2} ( t_{0} ) \mathrm {e}^{\frac {R_{2}}{L}t_{0}} \\[ 5pt ] \end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
i_{2} ( t ) &=&i_{2} ( t_{0} ) \mathrm {e}^{\frac {R_{2}}{L}t_{0}}\cdot \mathrm {e}^{-\frac {R_{2}}{L}t} \\[ 5pt ] &=&i_{2} ( t_{0} ) \mathrm {e}^{-\frac {R_{2}}{L} ( t-t_{0} ) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
$①$，$②$より，$ \ i_{1} ( t_{0} ) =i_{2} ( t_{0} ) \ $となるのは，
\[
\begin{eqnarray}
i_{1} ( t_{0} ) &=&i_{2} ( t_{0} ) \\[ 5pt ] \frac {E-v_{\mathrm {C}} ( t_{0} ) }{R_{1}} \mathrm {e}^{-\frac {1}{CR_{1}} ( t_{0} – t_{0} ) } &=&i_{2} ( t_{0} ) \mathrm {e}^{-\frac {R_{2}}{L} ( t_{0}-t_{0} ) } \\[ 5pt ] \frac {E-v_{\mathrm {C}} ( t_{0} ) }{R_{1}} &=&i_{2} ( t_{0} ) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヨ
$①$より，$ \ i_{1} ( t ) =0 \ $となる条件は，
\[
\begin{eqnarray}
i_{\mathrm {1}} ( t ) &=& 0 \\[ 5pt ] \frac {E-v_{\mathrm {C}} ( t_{0} ) }{R_{1}} \mathrm {e}^{-\frac {1}{CR_{1}} ( t – t_{0} ) } &=&0 \\[ 5pt ] \end{eqnarray}
\] であり，$ \ \displaystyle \mathrm {e}^{-\frac {1}{CR_{1}} ( t – t_{0} ) }　＞　0 \ $，$ \ R_{1}＞　0 \ $であるので，
\[
\begin{eqnarray}
E-v_{\mathrm {C}} ( t_{0} ) &=& 0 \\[ 5pt ] v_{\mathrm {C}} ( t_{0} ) &=&E \\[ 5pt ] \end{eqnarray}
\] と求められる。