《理論》〈電磁気〉[H28:問5] 平行平板コンデンサに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘電体が挿入された平行平板コンデンサに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

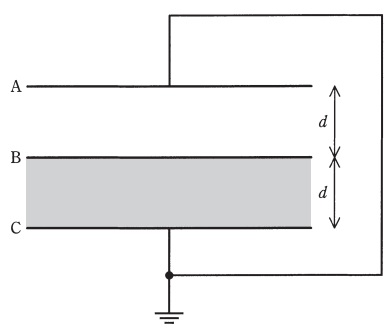
図のように，真空中に一辺の長さが$ \ l \ $の正方形で薄い平板電極$ \ 3 \ $枚が間隔$ \ d \ $で置かれた平行平板コンデンサがある。極板$ \ \mathrm {B} \ $－$ \ \mathrm {C} \ $間は，比誘電率$ \ \varepsilon _{r} \ $の誘電体で隙間なく満たされている。なお，真空中の誘電率は$ \ \varepsilon _{0} \ $とし，端効果は無視できるとする。
まず，全ての極板に何も接続しない状態では，極板$ \ \mathrm {A} \ $－$ \ \mathrm {B} \ $間の静電容量は$ \ \fbox {　（１）　} \ $であり，極板$ \ \mathrm {B} \ $－$ \ \mathrm {C} \ $間の静電容量は$ \ \fbox {　（２）　} \ $である。
次に，図のように，極板$ \ \mathrm {A} \ $及び$ \ \mathrm {C} \ $をともに接地し，極板$ \ \mathrm {B} \ $には電荷$ \ Q \ $を与える。このとき，極板$ \ \mathrm {A} \ $に誘導される電荷は$ \ \fbox {　（３）　} \ $，極板$ \ \mathrm {C} \ $に誘導される電荷は$ \ \fbox {　（４）　} \ $である。また，極板$ \ \mathrm {B} \ $の電位は$ \ \fbox {　（５）　} \ $である。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\varepsilon _{0}l^{3}}{d^{2}}　　　&（ロ）&　\frac {\varepsilon _{0}\varepsilon _{r}l^{2}}{d}　　　&（ハ）&　-\frac {1}{\varepsilon _{r}+1}Q \\[ 5pt ] &（ニ）&　-\frac {\varepsilon _{r}-2}{\varepsilon _{r}-1}Q　　　&（ホ）&　\frac {d}{\varepsilon _{0}\left( \varepsilon _{r}+1\right) l^{2}}Q　　　&（ヘ）&　\frac {d}{\varepsilon _{0}\left( \varepsilon _{r}-1\right) l^{2}}Q \\[ 5pt ] &（ト）&　\frac {\varepsilon _{0}l^{2}}{\varepsilon _{r} d}　　　&（チ）&　-\frac {\varepsilon _{r}}{\varepsilon _{r}+1}Q 　　　&（リ）&　\frac {\varepsilon _{r}l^{2}}{d} \\[ 5pt ] &（ヌ）&　\frac {\varepsilon _{r}l^{2}}{\varepsilon _{0}d}　　　&（ル）&　-\frac {1}{\varepsilon _{r}-1}Q　　　&（ヲ）&　\frac {\varepsilon _{0}l^{2}}{d}　 \\[ 5pt ] &（ワ）&　-\frac {1}{2}Q　　　&（カ）&　-Q　　　&（ヨ）&　\frac {d}{\varepsilon _{0}\varepsilon _{r}l^{2}}Q
\end{eqnarray}
\]

【ワンポイント解説】

本問は公式としては電験三種の内容で解くことができます。平行平板コンデンサの並列回路であることが分かればそれほど難しい問題ではないと思います。

1.平行平板コンデンサに関する諸公式
①静電容量$ \ C \ $のコンデンサに電圧$ \ V \ $がかかった時に各極板に現れる電荷$ \ Q \ $は，
\[
\begin{eqnarray}
Q&=&CV \\[ 5pt ] \end{eqnarray}
\] となります。

②極板間の誘電率$\varepsilon $，各極板の面積$S$，極板間の距離$d$とすると，このコンデンサの静電容量$C$は，
\[
\begin{eqnarray}
C&=&\frac {\varepsilon S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

③平行平板コンデンサに比誘電率$\varepsilon _{r}$の誘電体を挿入した時の誘電率$\varepsilon $は，真空中の誘電率を$\varepsilon _{0}$とすると，
\[
\begin{eqnarray}
\varepsilon &=&\varepsilon _{r}\varepsilon _{0} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　平行平板コンデンサの静電容量まとめ

【解答】

(1)解答：ヲ
ワンポイント解説「1.平行平板コンデンサに関する諸公式②」より，極板$\mathrm {A}$－$\mathrm {B}$間の静電容量$C_{1}$は，面積が$l^{2}$であることに注意すると，
\[
\begin{eqnarray}
C_{1}&=&\frac {\varepsilon_{0} l^{2}}{d} \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ロ
ワンポイント解説「1.平行平板コンデンサに関する諸公式②③」より，極板$\mathrm {B}$－$\mathrm {C}$間の静電容量$C_{2}$は，
\[
\begin{eqnarray}
C_{2}&=&\frac {\varepsilon_{0} \varepsilon_{r} l^{2}}{d} \\[ 5pt ] \end{eqnarray}
\] となる。

(3)解答：ハ
(4)解答：チ
電極$\mathrm {B}$に電荷が与えられた時の回路は図1のように書き換えることができる。ただし，極板$\mathrm {A}$側のコンデンサに蓄えられる電荷を$Q_{1}$，極板$\mathrm {C}$側のコンデンサに蓄えられる電荷を$Q_{2}$としている。

図1において，２つのコンデンサに蓄えられる電荷の合計が$Q$であるから，
\[
\begin{eqnarray}
Q_{1}+Q_{2}&=&Q　・・・① \\[ 5pt ] \end{eqnarray}
\] となる。また，両コンデンサ間の電圧は等しいので，
\[
\begin{eqnarray}
\frac {Q_{1}}{C_{1}}&=&\frac {Q_{2}}{C_{2}} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$C_{2}=\varepsilon_{r}C_{1}$であるから，
\[
\begin{eqnarray}
&&\frac {Q_{1}}{C_{1}}&=&\frac {Q_{2}}{\varepsilon_{r}C_{1}} \\[ 5pt ] &⇔&Q_{1}&=&\frac {Q_{2}}{\varepsilon_{r}}　・・・②
\end{eqnarray}
\] となる。①と②の連立方程式を解くと，
\[
\begin{eqnarray}
Q_{1}&=&\frac {1}{\varepsilon _{r}+1}Q \\[ 5pt ] Q_{2}&=&\frac {\varepsilon _{r}}{\varepsilon _{r}+1}Q
\end{eqnarray}
\] と求められる。極板$\mathrm {A}$に蓄えられる電荷は$-Q_{1}$，極板$\mathrm {C}$に蓄えられる電荷は$-Q_{2}$なので，
\[
\begin{eqnarray}
-Q_{1}&=&-\frac {1}{\varepsilon _{r}+1}Q \\[ 5pt ] -Q_{2}&=&-\frac {\varepsilon _{r}}{\varepsilon _{r}+1}Q
\end{eqnarray}
\] となる。

(5)解答：ホ
極板$\mathrm {B}$の電位$V$は，各コンデンサ間の電圧に等しいので，
\[
\begin{eqnarray}
V&=&\frac {Q_{1}}{C_{1}} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{\varepsilon _{r}+1}Q}{\displaystyle \frac {\varepsilon_{0} l^{2}}{d}} \\[ 5pt ] &=&\frac {d}{\varepsilon _{0}\left( \varepsilon _{r}+1\right) l^{2}}Q　
\end{eqnarray}
\] と求められる。