【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,影像(鏡像)電荷を用いた静電界解析に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,電位は無限遠点を基準とする。
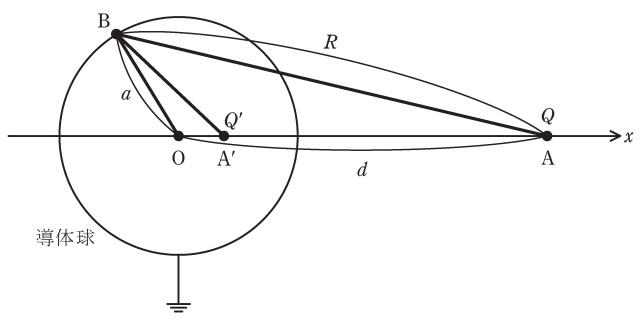
誘電率\( \ \varepsilon _{0} \ \)の真空中に半径\( \ a \ \)の接地された導体球が存在する。図のように,導体球の中心が原点\( \ \mathrm {O} \ \)となるように\( \ x \ \)軸を定め,\( \ x \ \)軸上の\( \ x=d \ \)の点\( \ \mathrm {A} \ \)に電荷\( \ Q \ \)の点電荷を置く(ただし\( \ d>a \ \)である)。このとき導体球が真空中に作り出す電界を影像電荷によって表現しよう。
導体球は接地されているので,導体球の表面のあらゆる点で電位が零になるという境界条件を満たす必要がある。そこで,図に示す導体球表面の点\( \ \mathrm {B} \ \)で境界条件を満たすように,導体球の代わりにその内部の\( \ x \ \)軸上の点\( \ \mathrm {A}^{\prime } \ \)に影像電荷\( \ Q^{\prime } \ \)を置く。
まず,点\( \ \mathrm {A}^{\prime } \ \)の\( \ x \ \)座標を\( \ x= \ \fbox { (1) } \ \)とすると,\( \ △\mathrm {AOB} \ \)と\( \ △\mathrm {BOA}^{\prime } \ \)が相似となる。辺\( \ \mathrm {AB} \ \)の長さを\( \ R \ \)とすると,点\( \ \mathrm {A} \ \)の点電荷が点\( \ \mathrm {B} \ \)に作り出す電位は\( \ \fbox { (2) } \ \)となるので,\( \ Q^{\prime }= \ \fbox { (3) } \ \)とすることによって,点\( \ \mathrm {B} \ \)で境界条件が満たされる。相似条件は導体球表面の任意の点について成立するので,点電荷と影像電荷によって導体球表面のあらゆる点で境界条件を満たすことができ,影像電荷が真空領域に作り出す電界は,導体球が作る電界と一致する。ガウスの法則から,点電荷によって導体球に誘起された電荷の総量は,影像電荷と同じ\( \ Q^{\prime } \ \)となる。
さらに\( \ x=-d \ \)の点に電荷\( \ -Q \ \)の点電荷を置く場合には,\( \ x= \ \fbox { (4) } \ \)の地点に影像電荷を追加することによって,真空中の電界を表現することができる。このとき,二つの点電荷によって導体球に誘起される総電荷は\( \ \fbox { (5) } \ \)となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {a^{2}}{d-a} &(ロ)& \frac {Q}{4\pi \varepsilon _{0}}\frac {1}{R} &(ハ)& \frac {a^{2}}{d} \\[ 5pt ]
&(ニ)& -\frac {d^{2}}{a} &(ホ)& -\frac {a^{2}}{d-a} &(ヘ)& \frac {Q}{4\pi \varepsilon _{0}}\frac {a}{R^{2}} \\[ 5pt ]
&(ト)& \frac {d^{2}}{a} &(チ)& \frac {a}{d}Q &(リ)& -\frac {a}{d-a}Q \\[ 5pt ]
&(ヌ)& \frac {2a}{d}Q &(ル)& -\frac {a}{d}Q &(ヲ)& -\frac {2a}{d}Q \\[ 5pt ]
&(ワ)& \frac {Q}{4\pi \varepsilon _{0}}\frac {1}{R^{2}} &(カ)& 0 &(ヨ)& -\frac {a^{2}}{d} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
静電界の影像電荷に関する問題です。
2種の場合,基本問題にするとほとんどの受験生が解けてしまうため,やや数学的な内容が含まれています。
(2)以外は連動した内容なので,(1)の計算を丁寧に行い間違えないように注意しましょう。
1.電界の強さ\( \ E \ \)
真空中で\( \ Q \ \)が作る電界の大きさ\( \ E \ \)は,距離\( \ r \ \)の地点で,
\[
\begin{eqnarray}
E&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.点電荷の作る電位\( \ V \ \)
真空中で\( \ Q \ \)が作る電位\( \ V \ \)は,電界の強さ\( \ E \ \)より,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r} E \mathrm {d}r \\[ 5pt ]
&=&-\int _{\infty }^{r} \frac {Q}{4\pi \varepsilon _{0}r^{2}} \mathrm {d}r \\[ 5pt ]
&=&-\left[ -\frac {Q}{4\pi \varepsilon _{0}r}\right] _{\infty }^{r} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ハ
題意より,\( \ △\mathrm {AOB} \ \)と\( \ △\mathrm {BOA}^{\prime } \ \)が相似となるので,
\[
\begin{eqnarray}
\frac {\mathrm {AO}}{\mathrm {BO}}&=&\frac {\mathrm {OB}}{\mathrm {OA}^{\prime }} \\[ 5pt ]
\frac {d}{a}&=&\frac {a}{x} \\[ 5pt ]
xd&=&a^{2} \\[ 5pt ]
x&=&\frac {a^{2}}{d} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ロ
点\( \ \mathrm {A} \ \)の点電荷\( \ Q \ \)が点\( \ \mathrm {B} \ \)に作り出す電位\( \ V_{\mathrm {A}} \ \)は,ワンポイント解説「2.点電荷の作る電位\( \ V \ \)」より,
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&\frac {Q}{4\pi \varepsilon _{0}R} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}}\frac {1}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ル
\( \ △\mathrm {AOB} \ \)と\( \ △\mathrm {BOA}^{\prime } \ \)が相似なので,線分\( \ \mathrm {BA}^{\prime } \ \)の長さを\( \ r \ \)とすると,
\[
\begin{eqnarray}
\frac {\mathrm {AO}}{\mathrm {BO}}&=&\frac {\mathrm {AB}}{\mathrm {BA}^{\prime }} \\[ 5pt ]
\frac {d}{a}&=&\frac {R}{r} \\[ 5pt ]
r&=&\frac {a}{d}R \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,点\( \ \mathrm {A}^{\prime } \ \)の点電荷\( \ Q^{\prime } \ \)が点\( \ \mathrm {B} \ \)に作り出す電位\( \ V_{\mathrm {A}}^{\prime } \ \)は,ワンポイント解説「2.点電荷の作る電位\( \ V \ \)」より,
\[
\begin{eqnarray}
V_{\mathrm {A}}^{\prime }&=&\frac {Q^{\prime }}{4\pi \varepsilon _{0}r} \\[ 5pt ]
&=&\frac {Q^{\prime }}{4\pi \varepsilon _{0}}\frac {d}{aR} \\[ 5pt ]
\end{eqnarray}
\]
となる。問題図より,導体球は接地されているので,導体球表面の電位は零となるから,
\[
\begin{eqnarray}
V_{\mathrm {A}}+V_{\mathrm {A}}^{\prime }&=&0 \\[ 5pt ]
\frac {Q}{4\pi \varepsilon _{0}}\frac {1}{R}+\frac {Q^{\prime }}{4\pi \varepsilon _{0}}\frac {d}{aR}&=&0 \\[ 5pt ]
\frac {Q^{\prime }}{4\pi \varepsilon _{0}}\frac {d}{aR}&=&-\frac {Q}{4\pi \varepsilon _{0}}\frac {1}{R} \\[ 5pt ]
Q^{\prime }\cdot \frac {d}{a}&=&-Q \\[ 5pt ]
Q^{\prime }&=&-\frac {a}{d}Q \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
\( \ x=-d \ \)の点に電荷\( \ -Q \ \)の点電荷を置く場合,(1)と同様に考えれば,\( \ \displaystyle x=-\frac {a^{2}}{d} \ \)の地点に影像電荷\( \ \displaystyle Q^{\prime \prime }=\frac {a}{d}Q \ \)を追加すれば,導体球の表面における境界条件を満たし,真空中の電界を表現することができる。
(5)解答:カ
二つの点電荷\( \ Q^{\prime } \ \)及び\( \ Q^{\prime \prime } \ \)によって導体球に誘起される総電荷は,
\[
\begin{eqnarray}
Q^{\prime }+Q^{\prime \prime }&=&-\frac {a}{d}Q+\frac {a}{d}Q \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは