《理論》〈電気回路〉[R01:問2]直流及び交流の混在する回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，直流と交流が混在する回路の電流と電圧に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

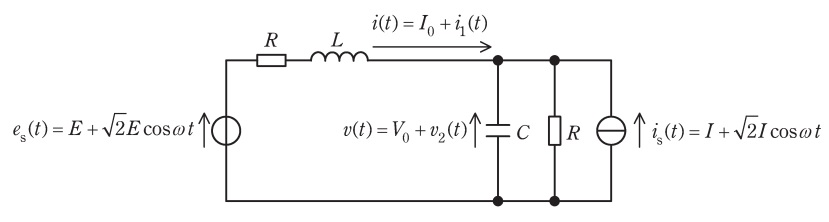
図のように，直流と角周波数$ \ \omega \ $の正弦波交流からなる理想電圧源$ \ e_{\mathrm {s}}\left( t \right) =E+\sqrt {2}E\cos \omega t \ $と理想電流源$ \ i_{\mathrm {s}}\left( t \right) =I+\sqrt {2}I\cos \omega t \ $が接続された回路を考える。定常状態での図の電流$ \ i\left( t \right) =I_{0}+i_{1}\left( t \right) \ $と電圧$ \ v\left( t \right) =V_{0}+v_{2}\left( t \right) \ $を求めたい。ただし，$ \ I_{0} \ $と$ \ V_{0} \ $は直流成分を，$ \ i_{1}\left( t \right) \ $と$ \ v_{2}\left( t \right) \ $は交流成分を表し，$ \ E＞0 \ $，$ \ I＞0 \ $とする。

回路の直流解析を行うと，重ねの理により$ \ I_{0}=\fbox {　（１）　} \ $，$ \ V_{0}=\fbox {　（２）　} \ $となる。

次に実効値を用いて，$ \ e_{\mathrm {s}}\left( t \right) \ $，$ \ i_{\mathrm {s}}\left( t \right) \ $の交流成分の複素表示及び$ \ i_{1}\left( t \right) \ $，$ \ v_{2}\left( t \right) \ $の複素表示を，それぞれ$ \ \dot E \ $，$ \ \dot I \ $及び$ \ {\dot I}_{1} \ $，$ \ {\dot V}_{2} \ $とすると，回路の交流解析の結果は，
\[
\begin{eqnarray}
\begin{bmatrix} \dot E \\ \dot I \end{bmatrix}&=&\begin{bmatrix} \fbox {　（３）　} & 1 \\ -1 & \fbox {　（４）　} \end{bmatrix}\begin{bmatrix} {\dot I}_{1} \\ {\dot V}_{2} \end{bmatrix}　・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。この表現は$ \ 2 \ $端子対回路の$ \ \mathrm {H} \ $パラメータ表現に他ならない。ここで，$ \ \dot E=R\dot I \ $，$ \ R=\omega L \ $，$ \ \displaystyle \frac {1}{R}=\omega C \ $と仮定し，①式を解くと，
\[
\begin{eqnarray}
\begin{bmatrix} {\dot I}_{1} \\ {\dot V}_{2} \end{bmatrix}&=&\frac {1}{\left( 1+\mathrm {j}\right) ^{2}+1}\begin{bmatrix} \fbox {　（４）　} & -1 \\ 1 & \fbox {　（３）　} \end{bmatrix}\begin{bmatrix} \dot E \\ \dot I \end{bmatrix}=\frac {1}{1+\mathrm {j}2}\begin{bmatrix} \mathrm {j}\dot I \\ \left( 2+\mathrm {j} \right) \dot E \end{bmatrix}　・・・　② \\[ 5pt ] \end{eqnarray}
\] を得る。②式の結果を利用すると，交流電圧$ \ v_{2}\left( t \right) \ $は$ \ v_{2}\left( t \right) =\fbox {　（５）　} \ $となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\sqrt {2}E\cos \left( \omega t-\tan ^{-1}\frac {3}{4}\right)　　　&（ロ）&　\frac {1}{R}+\mathrm {j}\omega C　　　&（ハ）&　E\cos \left( \omega t-\tan ^{-1}\frac {4}{3}\right) \\[ 5pt ] &（ニ）&　\frac {E}{2}-\frac {RI}{2}　　　&（ホ）&　\frac {E}{2R}+\frac {I}{2}　　　&（ヘ）&　\mathrm {j}\omega L+\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &（ト）&　\frac {RI}{2}　　　&（チ）&　\frac {R}{1+\mathrm {j}\omega CL}　　　　&（リ）&　R+\mathrm {j}\omega L \\[ 5pt ] &（ヌ）&　\mathrm {j}\omega C+\frac {1}{\mathrm {j}\omega L}　　　&（ル）&　\frac {E}{2}+\frac {RI}{2}　　　&（ヲ）&　\sqrt {2}E\cos \left( \omega t+\tan ^{-1}\frac {4}{3}\right) \\[ 5pt ] &（ワ）&　\frac {E}{2R}-\frac {I}{2}　　　&（カ）&　\frac {E}{2R}　　　&（ヨ）&　\frac {1}{R+\mathrm {j}\omega L} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電磁気の基本公式と平行平板コンデンサの特徴を理解しているかを問う問題となっています。本問を解くのにはたくさんの公式を理解している必要があり，3種より高度な問題となっていると言えるでしょう。

1.重ね(重ね合わせ)の理
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。
また，直流分に対しては，リアクトルは短絡，コンデンサは開放と考えます。
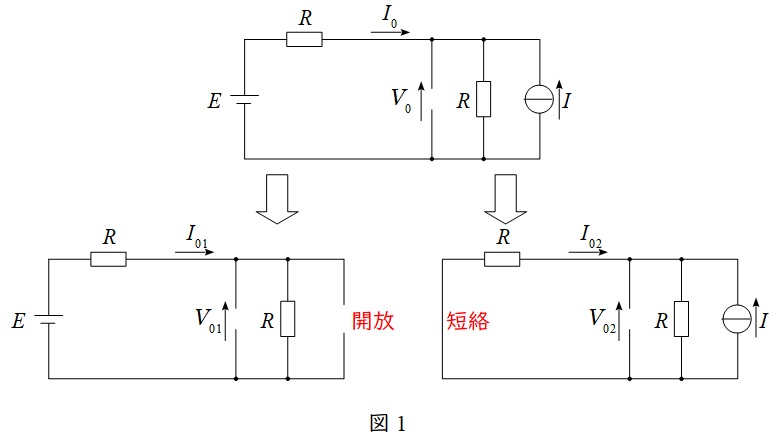
本問の直流分に対する回路は図1のようになります。

2.逆行列$ \ \boldsymbol A^{-1} \ $
ある行列$ \ \displaystyle \boldsymbol A =\begin{bmatrix} a & b \\ c & d \end{bmatrix} \ $が与えられているとき，$ \ \boldsymbol A \ $の逆行列$ \ \boldsymbol A^{-1} \ $は
\[
\begin{eqnarray}
\boldsymbol A^{-1} &=& \frac {1}{ad-bc}\begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

(1)解答：ワ
(2)解答：ル
ワンポイント解説「1.重ね(重ね合わせ)の理」の通り，直流分の回路は図1のように分解できる。
図1左図より，
\[
\begin{eqnarray}
I_{01} &=& \frac {E}{2R} \\[ 5pt ] V_{01} &=& \frac {R}{R+R}E \\[ 5pt ] &=& \frac {E}{2} \\[ 5pt ] \end{eqnarray}
\] であり，図1右図より，
\[
\begin{eqnarray}
I_{02} &=& \frac {R}{R+R}\times \left( -I\right) \\[ 5pt ] &=& -\frac {I}{2} \\[ 5pt ] V_{02} &=& R\times \frac {I}{2} \\[ 5pt ] &=& \frac {RI}{2} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
I_{0} &=& I_{01}+I_{02} \\[ 5pt ] &=& \frac {E}{2R}-\frac {I}{2} \\[ 5pt ] V_{0} &=& V_{01}+V_{02} \\[ 5pt ] &=& \frac {E}{2}+\frac {RI}{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
(4)解答：ロ
回路方程式より，
\[
\begin{eqnarray}
\dot E &=& R{\dot I}_{1}+\mathrm {j}\omega L{\dot I}_{1}+{\dot V}_{2} \\[ 5pt ] &=& \left( R+\mathrm {j}\omega L\right) {\dot I}_{1}+{\dot V}_{2} \\[ 5pt ] \dot I &=& -{\dot I}_{1}+\mathrm {j}\omega C {\dot V}_{2}+\frac {{\dot V}_{2}}{R} \\[ 5pt ] &=& -{\dot I}_{1}+\left( \frac {1}{R}+\mathrm {j}\omega C\right) {\dot V}_{2} \\[ 5pt ] \end{eqnarray}
\] であるから，行列表記すると，
\[
\begin{eqnarray}
\begin{bmatrix} \dot E \\ \dot I \end{bmatrix}&=&\begin{bmatrix} R+\mathrm {j}\omega L & 1 \\ -1 & \frac {1}{R}+\mathrm {j}\omega C \end{bmatrix}\begin{bmatrix} {\dot I}_{1} \\ {\dot V}_{2} \end{bmatrix} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：イ
$ \ \dot E=R\dot I \ $，$ \ R=\omega L \ $，$ \ \displaystyle \frac {1}{R}=\omega C \ $と仮定すると，①式は，
\[
\begin{eqnarray}
\begin{bmatrix} \dot E \\ \dot I \end{bmatrix}&=&\begin{bmatrix} R+\mathrm {j}R & 1 \\ -1 & \frac {1}{R}+\mathrm {j}\frac {1}{R} \end{bmatrix}\begin{bmatrix} {\dot I}_{1} \\ {\dot V}_{2} \end{bmatrix} \\[ 5pt ] &=&\begin{bmatrix} R\left( 1+\mathrm {j}\right) & 1 \\ -1 & \frac {1}{R}\left( 1+\mathrm {j}\right) \end{bmatrix}\begin{bmatrix} {\dot I}_{1} \\ {\dot V}_{2} \end{bmatrix} \\[ 5pt ] \end{eqnarray}
\] であり，ワンポイント解説「2.逆行列$ \ \boldsymbol A^{-1} \ $」より，
\[
\begin{eqnarray}
\begin{bmatrix} R\left( 1+\mathrm {j}\right) & 1 \\ -1 & \frac {1}{R}\left( 1+\mathrm {j}\right) \end{bmatrix}^{-1}&=&\frac {1}{R\left( 1+\mathrm {j}\right) \cdot \frac {1}{R}\left( 1+\mathrm {j}\right) +1}\begin{bmatrix} \frac {1}{R}\left( 1+\mathrm {j}\right) & -1 \\ 1 & R\left( 1+\mathrm {j}\right) \end{bmatrix} \\[ 5pt ] &=&\frac {1}{\left( 1+\mathrm {j}\right) ^{2} +1}\begin{bmatrix} \frac {1}{R}\left( 1+\mathrm {j}\right) & -1 \\ 1 & R\left( 1+\mathrm {j}\right) \end{bmatrix} \\[ 5pt ] &=&\frac {1}{1+\mathrm {j}2}\begin{bmatrix} \frac {1}{R}\left( 1+\mathrm {j}\right) & -1 \\ 1 & R\left( 1+\mathrm {j}\right) \end{bmatrix} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\begin{bmatrix} {\dot I}_{1} \\ {\dot V}_{2} \end{bmatrix}&=&\frac {1}{1+\mathrm {j}2}\begin{bmatrix} \frac {1}{R}\left( 1+\mathrm {j}\right) & -1 \\ 1 & R\left( 1+\mathrm {j}\right) \end{bmatrix}\begin{bmatrix} \dot E \\ \dot I \end{bmatrix} \\[ 5pt ] &=&\frac {1}{1+\mathrm {j}2}\begin{bmatrix} \frac {\dot E}{R}\left( 1+\mathrm {j}\right) -\dot I \\ \dot E + R\dot I\left( 1+\mathrm {j}\right) \end{bmatrix} \\[ 5pt ] &=&\frac {1}{1+\mathrm {j}2}\begin{bmatrix} \dot I\left( 1+\mathrm {j}\right) -\dot I \\ \dot E + \dot E\left( 1+\mathrm {j}\right) \end{bmatrix} \\[ 5pt ] &=&\frac {1}{1+\mathrm {j}2}\begin{bmatrix} \mathrm {j}\dot I \\ \left( 2+\mathrm {j} \right) \dot E \end{bmatrix} \\[ 5pt ] \end{eqnarray}
\] となり，これより，
\[
\begin{eqnarray}
{\dot V}_{2}&=&\frac {1}{1+\mathrm {j}2}\times \left( 2+\mathrm {j} \right) \dot E \\[ 5pt ] &=&\frac {1-\mathrm {j}2}{5}\times \left( 2+\mathrm {j} \right) \dot E \\[ 5pt ] &=&\frac {4-\mathrm {j}3}{5} \dot E \\[ 5pt ] \end{eqnarray}
\] となる。よって，$ \ {\dot V}_{2} \ $は$ \ \dot E \ $より，$ \ \displaystyle \frac {3}{4} \ \mathrm {[rad]} \ $だけ遅れるので，
\[
\begin{eqnarray}
v_{2}\left( t \right) &=&\sqrt {2}E\cos \left( \omega t-\tan ^{-1}\frac {3}{4}\right)
\end{eqnarray}
\] と求められる。