Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,静電界による電子の運動に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
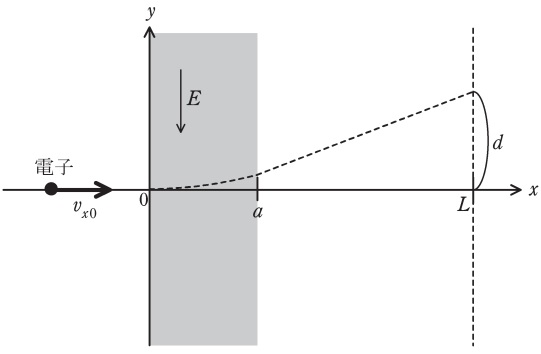
図のように,真空中を電子(質量\( \ m \ \),電荷量\( \ -e \ \),\( \ e\gt 0 \ \))が\( \ x \ \)軸上を\( \ x\lt 0 \ \)の領域から一定速度\( \ v_{\mathrm {x0}}\left( \gt 0\right) \ \)で運動している。領域\( \ 0 ≦ x ≦ a \ \)には,図に示すように\( \ y \ \)軸の負の方向に均一な電界\( \ E\left( \gt 0\right) \ \)がかかっており,それ以外の領域では電界がないものとする。電子の\( \ x \ \)座標が\( \ x=0 \ \)から\( \ x=a \ \)に達するまでにかかる時間は\( \ \fbox { (1) } \ \)である。領域\( \ 0 ≦ x ≦ a \ \)では,電子は電界から力\( \ F= \ \fbox { (2) } \ \)を受けて\( \ y \ \)方向に偏向する。運動の第\( \ 2 \ \)法則から\( \ y \ \)方向の運動方程式は\( \ \displaystyle m\frac {\mathrm {d}v_{\mathrm {y}}}{\mathrm {d}t}= \ \fbox { (2) } \ \)と表される。ただし,\( \ v_{\mathrm {y}} \ \)は速度の\( \ y \ \)方向成分を表す。微分方程式を解くことにより,電子の\( \ x \ \)座標が\( \ x=a \ \)に到達したときの\( \ v_{\mathrm {y}} \ \)は\( \ \fbox { (3) } \ \)となり,そのときの電子の\( \ y \ \)座標は\( \ \fbox { (4) } \ \)となる。領域\( \ x\gt a \ \)では,電子の運動は\( \ x \ \),\( \ y \ \)方向共に等速度運動となることから,電子が\( \ x=L\left( \gt a\right) \ \)に到達した際の\( \ y \ \)座標を\( \ d \ \)とすると,\( \ d = \ \fbox { (5) } \ \)となる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {eE}{m}\left( \frac {a}{v_{\mathrm {x0}}}\right) ^{2} &(ロ)& \frac {eE}{2m}\frac {a\left( 2L-a\right) }{v_{\mathrm {x0}}^{2}} &(ハ)& \frac {eE}{m} \frac {a}{v_{\mathrm {x0}}} \\[ 5pt ]
&(ニ)& \frac {eE}{2m}\frac {a\left( L-a\right) }{v_{\mathrm {x0}}^{2}} &(ホ)& \frac {m}{eE} \frac {L-a}{v_{\mathrm {x0}}} &(ヘ)& eE \\[ 5pt ]
&(ト)& \frac {eE}{m} \frac {v_{\mathrm {x0}}}{a} &(チ)& \frac {eE}{m} &(リ)& \frac {a}{v_{\mathrm {x0}}} \\[ 5pt ]
&(ヌ)& \frac {L}{v_{\mathrm {x0}}} &(ル)& \frac {eE}{2m}\left( \frac {a}{v_{\mathrm {x0}}}\right) ^{2} &(ヲ)& \frac {eE}{m}\frac {a\left( 2L-a\right) }{v_{\mathrm {x0}}^{2}} \\[ 5pt ]
&(ワ)& aE &(カ)& \frac {L-a}{v_{\mathrm {x0}}} &(ヨ)& \frac {eE}{2m}\left( \frac {L}{v_{\mathrm {x0}}}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電界中の電子の動きに関する問題です。
少し計算量の多い問題ですが,得意な方は非常に易しく感じる問題なので,受験生の点数差が非常に開きやすい問題と言えます。
1.電荷に働く力の大きさ
一様な電界\( \ E \ \)が電荷\( \ q \ \)にかかっているとき,この電荷\( \ q \ \)に働く力の大きさ\( \ F \ \)は,
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.運動方程式(力学)
質量\( \ m \ \)の物体に力\( \ F \ \)がかかっている時,この物体にかかる加速度\( \ a \ \)との間には,
\[
\begin{eqnarray}
F &=&ma \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
3.物体の運動に関する公式(力学)
初速度が\( \ v_{0} \ \mathrm {[m/s]} \ \)の物体が加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)で運動している時,\( \ t \ \mathrm {[s]} \ \) 後の物体の速度は,
\[
\begin{eqnarray}
v&=&v_{0}+at \\[ 5pt ]
\end{eqnarray}
\]
となります。
また,基準となる位置\( \ x_{0} \ \mathrm {[m]} \ \)にある物体が,初速度\( \ v_{0} \ \mathrm {[m/s]} \ \),加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)で運動しているとすると,時刻\( \ t \ \mathrm {[s]} \ \)後の位置\( \ x \ \mathrm {[m]} \ \)は,
\[
\begin{eqnarray}
x &=&x_{0}+v_{0}t+\frac {1}{2}at^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:リ
\( \ x \ \)軸方向には電界がかかっておらず,電子の速度の\( \ x \ \)方向成分は一定である。したがって,\( \ x=0 \ \)から\( \ x=a \ \)に達するまでにかかる時間\( \ t_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
t_{\mathrm {a}}&=&\frac {a}{v_{\mathrm {x0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヘ
電子\( \ -e \ \)にかかる力は電界の向きが\( \ -y \ \)方向なので\( \ +y \ \)方向となり,その大きさ\( \ F \ \)は,ワンポイント解説「1.電荷に働く力の大きさ」の通り,
\[
\begin{eqnarray}
F&=&eE \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ハ
問題に与えられている微分方程式を変形すると,
\[
\begin{eqnarray}
m\frac {\mathrm {d}v_{\mathrm {y}}}{\mathrm {d}t}&=&eE \\[ 5pt ]
\mathrm {d}v_{\mathrm {y}}&=&\frac {eE}{m}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺積分すると,(1)より上式が成立するのは\( \ \displaystyle 0≦t≦\frac {a}{v_{\mathrm {x0}}} \ \)であるから,
\[
\begin{eqnarray}
m\frac {\mathrm {d}v_{\mathrm {y}}}{\mathrm {d}t}&=&eE \\[ 5pt ]
v_{\mathrm {y}}&=&\int _{0}^{\frac {a}{v_{\mathrm {x0}}}}\frac {eE}{m}\mathrm {d}t \\[ 5pt ]
&=&\left[ \frac {eE}{m}t\right] _{0}^{\frac {a}{v_{\mathrm {x0}}}} \\[ 5pt ]
&=&\frac {eE}{m} \frac {a}{v_{\mathrm {x0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
【別解】
ワンポイント解説「2.運動方程式(力学)」より,加速度\( \ \alpha \ \)とすると,
\[
\begin{eqnarray}
F&=&m\alpha \\[ 5pt ]
eE&=&m\alpha \\[ 5pt ]
\alpha &=&\frac {eE}{m} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ x=a \ \)での速度\( \ v_{\mathrm {y}} \ \)は,\( \ y \ \)方向の初速度が\( \ 0 \ \)であるので,ワンポイント解説「3.物体の運動に関する公式(力学)」の通り,
\[
\begin{eqnarray}
v_{\mathrm {y}}&=&\alpha t \\[ 5pt ]
&=&\frac {eE}{m} \frac {a}{v_{\mathrm {x0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
\( \ \displaystyle \frac {\mathrm {d}y}{\mathrm {d}t}=v_{\mathrm {y}} \ \)であるから,
\[
\begin{eqnarray}
\mathrm {d}y&=&v_{\mathrm {y}}\mathrm {d}t \\[ 5pt ]
&=&\frac {eE}{m} t\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺積分すると,\( \ x=a \ \)での位置\( \ y_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
y_{\mathrm {a}}&=&\int _{0}^{\frac {a}{v_{\mathrm {x0}}}}\frac {eE}{m} t\mathrm {d}t \\[ 5pt ]
&=&\frac {eE}{m} \left[ \frac {t^{2}}{2} \right] _{0}^{\frac {a}{v_{\mathrm {x0}}}} \\[ 5pt ]
&=&\frac {eE}{2m}\left( \frac {a}{v_{\mathrm {x0}}}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
【別解】
\( \ x=a \ \)での位置\( \ y_{\mathrm {a}} \ \)は,\( \ y \ \)方向の初期位置が\( \ 0 \ \),初速度が\( \ 0 \ \)であるので,ワンポイント解説「3.物体の運動に関する公式(力学)」の通り,
\[
\begin{eqnarray}
y_{\mathrm {a}}&=&\frac {1}{2}\alpha t^{2} \\[ 5pt ]
&=&\frac {1}{2}\frac {eE}{m} \left( \frac {a}{v_{\mathrm {x0}}}\right) ^{2} \\[ 5pt ]
&=&\frac {eE}{2m}\left( \frac {a}{v_{\mathrm {x0}}}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ロ
電子の速度の\( \ x \ \)方向成分は一定であるため,\( \ x=a \ \)から\( \ x=L \ \)に達するまでにかかる時間\( \ t_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
t_{\mathrm {L}}&=&\frac {L-a}{v_{\mathrm {x0}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ x=a \ \)以降は電子の速度の\( \ y \ \)方向成分も一定であるため,
\[
\begin{eqnarray}
d&=&y_{\mathrm {a}}+v_{\mathrm {y}}t_{\mathrm {L}} \\[ 5pt ]
&=&\frac {eE}{2m}\left( \frac {a}{v_{\mathrm {x0}}}\right) ^{2}+\frac {eE}{m} \frac {a}{v_{\mathrm {x0}}}\cdot \frac {L-a}{v_{\mathrm {x0}}} \\[ 5pt ]
&=&\frac {eE}{2m}\left\{ \frac {a^{2}}{v_{\mathrm {x0}}^{2}}+ \frac {2a\left( L-a \right) }{v_{\mathrm {x0}}^{2}}\right\} \\[ 5pt ]
&=&\frac {eE}{2m} \frac {a^{2}+2aL-2a^{2}}{v_{\mathrm {x0}}^{2}} \\[ 5pt ]
&=&\frac {eE}{2m} \frac {2aL-a^{2}}{v_{\mathrm {x0}}^{2}} \\[ 5pt ]
&=&\frac {eE}{2m}\frac {a\left( 2L-a\right) }{v_{\mathrm {x0}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは