《理論》〈電気回路〉[R03:問7]発光ダイオード（ＬＥＤ）の点灯回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，発光ダイオード$ \ \left( \mathrm {LED}\right) \ $の点灯回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。ただし，$ \ \mathrm {LED} \ $の明るさは$ \ \mathrm {LED} \ $を流れる電流に比例するとする。

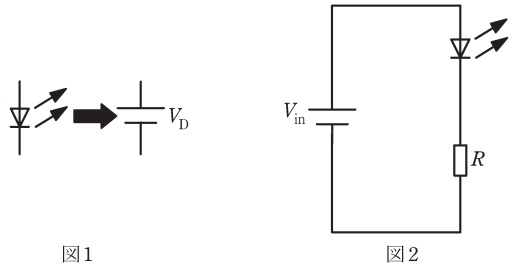
点灯時の$ \ \mathrm {LED} \ $の順方向電圧$ \ V_{\mathrm {D}} \ $はほぼ一定値となる。このため点灯時の$ \ \mathrm {LED} \ $の解析は，$ \ \mathrm {LED} \ $を図1のように大きさ$ \ V_{\mathrm {D}} \ $の直流電圧源で置き換えて考えると簡略化できる。

まず，図2の回路を用いて$ \ \mathrm {LED} \ $を点灯させた。$ \ \mathrm {LED} \ $に直列に接続する抵抗$ \ R \ $の役割は$ \ \fbox {　（１）　} \ $である。$ \ \mathrm {LED} \ $を流れる電流は$ \ \mathrm {LED} \ $を直流電圧源$ \ V_{\mathrm {D}} \ $に置き換えることで$ \ \fbox {　（２）　} \ $と求められる。

次に，$ \ 2 \ $個の$ \ \mathrm {LED} \ $を点灯させるために図3及び図4の回路を作製した。このとき図3及び図4で用いた全ての$ \ \mathrm {LED} \ $の特性は等しく，$ \ V_{\mathrm {D}} \ $は全て$ \ 2 \ \mathrm {V} \ $とする。図3の$ \ V_{\mathrm {in}} \ $が$ \ 5 \ \mathrm {V} \ $であるとき図3の$ \ \mathrm {LED} \ $を流れる電流を$ \ 50 \ \mathrm {mA} \ $とするためには図3の抵抗$ \ R \ $を$ \ \fbox {　（３）　} \ \mathrm {\Omega } \ $とすればよい。図3と図4の抵抗$ \ R \ $を$ \ \fbox {　（３）　} \ \mathrm {\Omega } \ $とし，図3と図4の全ての$ \ \mathrm {LED} \ $の明るさが等しくなるように図4の$ \ V_{\mathrm {in}} \ $を調整した。このとき図4の回路の消費電力は$ \ \fbox {　（４）　} \ \mathrm {mW} \ $である。

図3及び図4の$ \ 2 \ $個の$ \ \mathrm {LED} \ $のうち片方の$ \ \mathrm {LED} \ $が破損し断線したときにも，もう一方の$ \ \mathrm {LED} \ $が点灯し続けるのは$ \ \fbox {　（５）　} \ $である。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　300　　　　　&（ロ）&　500　　　　　&（ハ）&　\mathrm {LED} \ の破損防止 \\[ 5pt ] &（ニ）&　250　　　　　&（ホ）&　図 \ 3　　　　　&（ヘ）&　60 \\[ 5pt ] &（ト）&　20　　　　　&（チ）&　\frac {V_{\mathrm {in}}+V_{\mathrm {D}}}{R}　　　　　&（リ）&　図 \ 3 \ と \ 図 \ 4 \ の両方 \\[ 5pt ] &（ヌ）&　50　　　　　&（ル）&　\mathrm {LED} \ の保温　　　　　&（ヲ）&　\mathrm {LED} \ の明るさの向上 \\[ 5pt ] &（ワ）&　\frac {V_{\mathrm {in}}}{R}　　　　　&（カ）&　図 \ 4　　　　　&（ヨ）&　\frac {V_{\mathrm {in}}-V_{\mathrm {D}}}{R} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {LED} \ $を含む電気回路の計算問題です。
特別難解な公式を使用せず，キルヒホッフの法則を使って解く問題であるため，ぜひ完答を狙って頂きたい問題です。

【解答】

(1)解答：ハ
題意より解答候補は，（ハ）$ \ \mathrm {LED} \ $の破損防止，（ル）$ \ \mathrm {LED} \ $の保温，（ヲ）$ \ \mathrm {LED} \ $の明るさの向上，になると思います。
$ \ \mathrm {LED} \ $に直列に接続する抵抗$ \ R \ $は，$ \ \mathrm {LED} \ $が導通したときの過電流を抑えるための抵抗であり，目的は$ \ \mathrm {LED} \ $の破損防止となります。

(2)解答：ヨ
図2においてダイオードを図1の通り直流電圧源$ \ V_{\mathrm {D}} \ $に置き換え，回路を流れる電流を$ \ I_{2} \ \mathrm {[A]} \ $とすると，キルヒホッフの法則より，
\[
\begin{eqnarray}
V_{\mathrm {in}}-V_{\mathrm {D}}&=&RI_{2} \\[ 5pt ] I_{2}&=&\frac {V_{\mathrm {in}}-V_{\mathrm {D}}}{R} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
図3において回路を流れる電流$ \ I_{3} \ \mathrm {[A]} \ $とすると，キルヒホッフの法則より，
\[
\begin{eqnarray}
V_{\mathrm {in}}-2V_{\mathrm {D}}&=&RI_{3} \\[ 5pt ] \end{eqnarray}
\] であるから，$ \ V_{\mathrm {in}} = 5 \ \mathrm {[V]} \ $，$ \ V_{\mathrm {D}} = 2 \ \mathrm {[V]} \ $，$ \ I_{3}=50\times 10^{-3} \ \mathrm {[A]} \ $を代入すると，
\[
\begin{eqnarray}
5-2\times 2&=&R\times 50\times 10^{-3} \\[ 5pt ] R&=&20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：イ
図4の抵抗$ \ R \ $を流れる電流$ \ I_{4} \ \mathrm {[A]} \ $は，$ \ \mathrm {LED} \ $の明るさを一定としたため$ \ I_{4}=50\times 10^{-3} \ \mathrm {[A]} \ $である。キルヒホッフの法則より，
\[
\begin{eqnarray}
V_{\mathrm {in}}-V_{\mathrm {D}}&=&RI_{4} \\[ 5pt ] V_{\mathrm {in}}&=&V_{\mathrm {D}}+RI_{4} \\[ 5pt ] &=&2+20\times 50\times 10^{-3} \\[ 5pt ] &=&3 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。また，電源を流れる電流は$ \ 2I_{4}=100\times 10^{-3} \ \mathrm {[A]} \ $であるから，回路の消費電力$ \ P \ \mathrm {[mW]} \ $は，
\[
\begin{eqnarray}
P&=&V_{\mathrm {in}}\cdot 2I_{4} \\[ 5pt ] &=&3\times 100\times 10^{-3} \\[ 5pt ] &=&0.3 \ \mathrm {[W]}　→　300 \ \mathrm {[mW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
片方の$ \ \mathrm {LED} \ $が破損し断線したときに，もう一方の$ \ \mathrm {LED} \ $に電流が流れ続ける場合に$ \ \mathrm {LED} \ $は点灯し続けます。
したがって，点灯し続けるのは並列回路の図4のみとなります。