Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,演算増幅器に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
a 理想演算増幅器の差動電圧利得と同相電圧利得を\( \ \mathrm {dB} \ \)で表すと,\( \ \fbox { (1) } \ \)である。
b 演算増幅器を用いて増幅回路を実現する場合,通常,\( \ \fbox { (2) } \ \)増幅回路を構成して用いられる。演算増幅器を用いた\( \ \fbox { (2) } \ \)増幅回路において演算増幅器の\( \ 2 \ \)個の入力端子の\( \ \fbox { (3) } \ \)となることを仮想短絡と呼ぶ。
c 直流における差動電圧利得が\( \ 100 \ \mathrm {dB} \ \),遮断周波数が\( \ 10 \ \mathrm {Hz} \ \)の\( \ 1 \ \)次の周波数特性を有する演算増幅器がある。この演算増幅器の利得帯域幅積(\( \ \mathrm {GB} \ \)積)は,\( \ \fbox { (4) } \ \)である。遮断周波数以上の周波数では周波数が\( \ 10 \ \)倍に増加すると,演算増幅器の電圧利得は\( \ 20 \ \mathrm {dB} \ \)低下する。そのため,電圧利得が\( \ 0 \ \mathrm {dB} \ \)となる周波数(ユニティゲイン周波数)は\( \ \mathrm {GB} \ \)積と等しい。
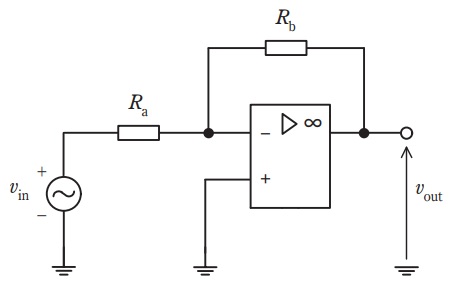
d 理想演算増幅器を用いた下図の回路の電圧増幅度\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は\( \ \fbox { (5) } \ \)である。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& -\frac {R_{\mathrm {b}}}{R_{\mathrm {a}}} &(ロ)& 1 \ \mathrm {kHz} &(ハ)& 1 \ \mathrm {MHz} \\[ 5pt ]
&(ニ)& \frac {R_{\mathrm {a}}+R_{\mathrm {b}}}{R_{\mathrm {a}}} &(ホ)& -\frac {R_{\mathrm {a}}}{R_{\mathrm {b}}} &(ヘ)& 100 \ \mathrm {kHz} \\[ 5pt ]
&(ト)& 負帰還 &(チ)& 正帰還 &(リ)& 無帰還 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ヌ)& 電位が回路構成によらず常に零 \\[ 5pt ]
&(ル)& 電流が回路構成によらず常に零 \\[ 5pt ]
&(ヲ)& 電位がほぼ等電位 \\[ 5pt ]
&(ワ)& ともに \ +\infty \\[ 5pt ]
&(カ)& 差動電圧利得が \ +\infty \ であり,同相電圧利得が \ -\infty \ \\[ 5pt ]
&(ヨ)& 同相電圧利得が \ +\infty \ であり,差動電圧利得が \ -\infty \ \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
演算増幅器に関する問題です。
通常は(5)の空欄の内容の問題が出題されることが多いですが,\( \ 2 \ \)種の受験生のレベルを考えて,ややこしく(1)や(4)の空欄を出題したような印象です。
内容は一度理解してしまえば難しくありませんので,本問で理解するようにしましょう。
1.理想的な演算増幅器の特徴
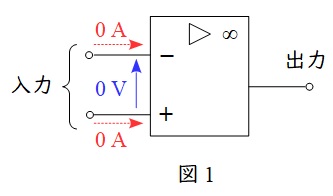
1.電圧増幅率が無限大である。したがって,無限大でない有限数が出力される時,入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
2.入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
3.出力インピーダンスがゼロである。
2.演算増幅器の電圧増幅率とゲインの関係
演算増幅器の電圧増幅率が\( \ \displaystyle \frac {V_{\mathrm {out}}}{V_{\mathrm {in}}} \ \)であるとき,ゲイン\( \ g \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| \frac {V_{\mathrm {out}}}{V_{\mathrm {in}}}\right| \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:カ
題意より解答候補は,(ワ)ともに\( \ +\infty \ \),(カ)差動電圧利得が\( \ +\infty \ \)であり,同相電圧利得が\( \ -\infty \ \),(ヨ)同相電圧利得が\( \ +\infty \ \)であり,差動電圧利得が\( \ -\infty \ \),になると思います。
理想演算増幅器において,入力端子間に電圧差がある差動利得は,
\[
\begin{eqnarray}
g&=&20\log _{10} \infty \\[ 5pt ]
&=&\infty \\[ 5pt ]
\end{eqnarray}
\]
となり,入力端子間に全く同じ電圧を入力する同相利得は,
\[
\begin{eqnarray}
g&=&20\log _{10} 0 \\[ 5pt ]
&=&-\infty \\[ 5pt ]
\end{eqnarray}
\]
となり,差動電圧利得が\( \ +\infty \ \)であり,同相電圧利得が\( \ -\infty \ \)となります。
(2)解答:ト
題意より解答候補は,(ト)負帰還,(チ)正帰還,(リ)無帰還,になると思います。
仮想短絡は,演算増幅器を用いた負帰還増幅回路において演算増幅器の「1.理想的な演算増幅器の特徴」を満たすものとなります。
(3)解答:ヲ
題意より解答候補は,(ヌ)電位が回路構成によらず常に零,(ル)電流が回路構成によらず常に零,(ヲ)電位がほぼ等電位,になると思います。
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り,仮想短絡(バーチャルショート)とは入力端子間の電位差がない,すなわち電位がほぼ等電位になることをいいます。
(4)解答:ハ
題意より解答候補は,(ロ)\( \ 1 \ \mathrm {kHz} \ \),(ハ)\( \ 1 \ \mathrm {MHz} \ \),(ヘ)\( \ 100 \ \mathrm {kHz} \ \),になると思います。
問題文の通り,「直流における差動電圧利得が\( \ 100 \ \mathrm {dB} \ \),遮断周波数が\( \ 10 \ \mathrm {Hz} \ \)」であり,「遮断周波数以上の周波数では周波数が\( \ 10 \ \)倍に増加すると,演算増幅器の電圧利得は\( \ 20 \ \mathrm {dB} \ \)低下」し,「電圧利得が\( \ 0 \ \mathrm {dB} \ \)となる周波数(ユニティゲイン周波数)は\( \ \mathrm {GB} \ \)積と等しい。」ので,
差動電圧利得が\( \ 100 \ \mathrm {dB} \ \)のとき,遮断周波数が\( \ 10 \ \mathrm {Hz} \ \)
差動電圧利得が\( \ 80 \ \mathrm {dB} \ \)のとき,遮断周波数が\( \ 10^{2} \ \mathrm {Hz} \ \)
差動電圧利得が\( \ 60 \ \mathrm {dB} \ \)のとき,遮断周波数が\( \ 10^{3} \ \mathrm {Hz} \ \)
差動電圧利得が\( \ 40 \ \mathrm {dB} \ \)のとき,遮断周波数が\( \ 10^{4} \ \mathrm {Hz} \ \)
差動電圧利得が\( \ 20 \ \mathrm {dB} \ \)のとき,遮断周波数が\( \ 10^{5} \ \mathrm {Hz} \ \)
差動電圧利得が\( \ 0 \ \mathrm {dB} \ \)のとき,遮断周波数が\( \ 10^{6} \ \mathrm {Hz} \ \)
すなわち利得帯域幅積(\( \ \mathrm {GB} \ \)積)は,\( \ 10^{6} \ \mathrm {[Hz]}=1 \ \mathrm {[MHz]} \ \)と求められます。
(5)解答:イ
演算増幅器の+側の入力端子は接地されているので,その電圧は\( \ V_{+}=0 \ \mathrm {[V]} \ \)であり,-側の入力端子の電圧\( \ V_{-} \ \mathrm {[V]} \ \)は理想演算増幅器においては仮想短絡(バーチャルショート)と考えられるので\( \ V_{-}=0 \ \mathrm {[V]} \ \)となる。
よって,\( \ R_{\mathrm {a}} \ \)を流れる電流\( \ I \ \mathrm {[A]} \ \)の大きさは,
\[
\begin{eqnarray}
I&=&\frac {v_{\mathrm {in}}-V_{-}}{R_{\mathrm {a}}} \\[ 5pt ]
&=&\frac {v_{\mathrm {in}}-0}{R_{\mathrm {a}}} \\[ 5pt ]
&=&\frac {v_{\mathrm {in}}}{R_{\mathrm {a}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,理想演算増幅器においては入力電流は零であるから,\( \ I \ \mathrm {[A]} \ \)はそのまま\( \ R_{\mathrm {b}} \ \)に流れる。したがって,\( \ v_{\mathrm {out}} \ \mathrm {[V]} \ \)を求める式より,
\[
\begin{eqnarray}
v_{\mathrm {out}}&=&V_{-}-R_{\mathrm {b}}I \\[ 5pt ]
&=&0-R_{\mathrm {b}}\cdot \frac {v_{\mathrm {in}}}{R_{\mathrm {a}}} \\[ 5pt ]
&=&-\frac {R_{\mathrm {b}}}{R_{\mathrm {a}}}v_{\mathrm {in}} \\[ 5pt ]
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&-\frac {R_{\mathrm {b}}}{R_{\mathrm {a}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは