《理論》〈電磁気〉[R06:問2]円柱導体内外の電磁界に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，円柱導体内外の電磁界に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

図のように，透磁率$ \ \mu \ $，導電率$ \ \sigma \ $の材料からなる半径$ \ a \ $の十分に長い円柱導体を考える。

大きさが$ \ I \ $の直流電流が，一様な密度で円柱導体に流れている場合，導体内で中心軸からの位置$ \ r\left( ≦a\right) \ $における磁界の強さは$ \ \fbox {　（１）　} \ $となる。$ \ r \ $における単位体積当たりの磁気エネルギーを$ \ w_{\mathrm {m}}\left( r\right) \ $とすると，微小幅$ \ \mathrm {d}r \ $，単位長さの円筒のもつエネルギーは$ \ w_{\mathrm {m}}\left( r\right) 2\pi r \mathrm {d}r \ $と表される。これを$ \ r=0～a \ $の範囲で積分することにより，円柱導体の内部に蓄えられる単位長さ当たりの磁気エネルギー$ \ W_{\mathrm {i}}= \ \fbox {　（２）　} \ $を求めることができる。

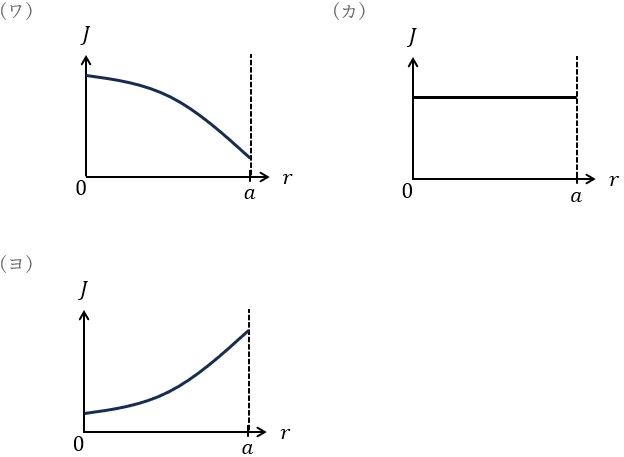
$ \ I \ $を流すために必要な電圧は，単位長さ当たり$ \ E_{\mathrm {DC}}= \ \fbox {　（３）　} \ $である。一方，実効値が$ \ I \ $と同じ大きさの交流電流を流すために必要な単位長さ当たりの交流電圧の実効値$ \ E_{\mathrm {AC}} \ $は，$ \ E_{\mathrm {DC}} \ $と$ \ \fbox {　（４）　} \ $の関係がある。周波数が高い場合，表皮効果により，導体断面における交流電流の電流密度$ \ J \ $は図$ \ \fbox {　（５）　} \ $のようになる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　E_{\mathrm {AC}}＜E_{\mathrm {DC}}　　　　&（ロ）&　E_{\mathrm {AC}}＞E_{\mathrm {DC}}　　　　&（ハ）&　E_{\mathrm {AC}}=E_{\mathrm {DC}} \\[ 5pt ] &（ニ）&　\frac {\mu I^{2}}{24\pi ^{2}a}　　　　&（ホ）&　\frac {I}{2\pi r}　　　　&（ヘ）&　\frac {\mu I}{8\pi } \\[ 5pt ] &（ト）&　\frac {\mu I^{2}}{32\pi ^{2}}　　　　&（チ）&　\frac {rI}{2\pi a^{2}}　　　　&（リ）&　\frac {\sigma I}{\pi a^{2}} \\[ 5pt ] &（ヌ）&　\frac {\mu I^{2}}{16\pi }　　　　&（ル）&　\frac {I}{\sigma \pi a^{2}}　　　　&（ヲ）&　\frac {rI}{\pi a^{2}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

導体に発生する磁界と表皮効果に関する問題です。
(1)と(2)の内容が$ \ 3 \ $種より高度な数学を要する問題です。$ \ 2 \ $種以上では定番の考え方となりますので，確実に理解しておくようにして下さい。

1.アンペア（アンペール）の周回積分の法則
空間上の磁界ベクトルを$ \ \boldsymbol H \ $，$ \ \mathrm {C} \ $を閉曲線，$ \ \mathrm {d}\boldsymbol l \ $を$ \ \mathrm {C} \ $上の微小区間ベクトル，$ \ I \ $を$ \ \mathrm {C} \ $と鎖交する電流の総量とすると，
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I　 \\[ 5pt ] \end{eqnarray}
\] の関係があり，これをアンペアの周回積分の法則といいます。
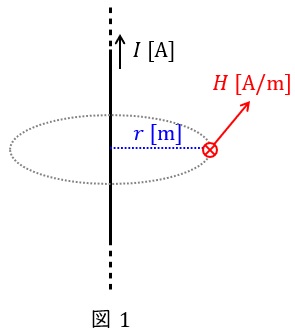
例えば，図1のように無限長直線電流$ \ I \ \mathrm {[A]} \ $が流れているとき，電線から距離$ \ r \ \mathrm {[m]} \ $の位置での磁界の強さ$ \ H \ \mathrm {[A / m]} \ $は，$ \ l=2\pi r \ $なので，
\[
\begin{eqnarray}
2\pi r H&=&I \\[ 5pt ] H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.導体の抵抗率及び導電率
導体の断面積$ \ 1 \ \mathrm {m^{2}} \ $，長さ$ \ 1 \ \mathrm {m} \ $あたりの抵抗値を抵抗率$ \ \rho \ \mathrm {[\Omega \cdot m ]} \ $といい，導体材料の電流の流れにくさを示す指標となります。また，抵抗率の逆数を導電率$ \ \sigma \ \mathrm {[S/m ]} \ $といい，導体材料の電流の流れやすさの指標となります。この導体における断面積$ \ S \ \mathrm {[m^{2}]} \ $，長さ$ \ l \ \mathrm {[m]} \ $の抵抗値$ \ R \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S}=\frac {l}{\sigma S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

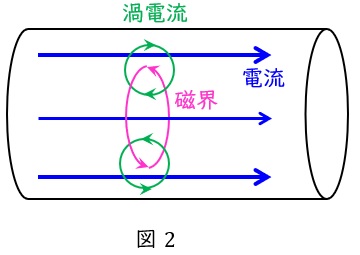
3.表皮効果
交流電流において，導体内を流れる電流によりアンペールの法則に沿った磁界が発生し，その発生した磁界の変化によりファラデーの電磁誘導の法則に沿った渦電流が発生することで，導体内の電流分布が外側に集中する現象です。
電線の断面積が大きい電線では無視できなくなり，角周波数と透磁率，導電率が大きくなるほど顕著となります。

4.エネルギー密度$ \ w \ $
一様電界中の電界の大きさが$ \ \boldsymbol E \ \mathrm {[V / m]} \ $，電束密度が$ \ \boldsymbol D \ \mathrm {[C / m^{2}]} \ $，誘電率が$ \ \varepsilon \ \mathrm {[F / m]} \ $であるとき，静電エネルギー密度$ \ w_{\mathrm {e}} \ \mathrm {[J / m^{3}]} \ $は，
\[
\begin{eqnarray}
w_{\mathrm {e}} &=&\frac {1}{2}\boldsymbol D\cdot \boldsymbol E \\[ 5pt ] &=&\frac {1}{2}\varepsilon \left| \boldsymbol E\right| ^{2} \\[ 5pt ] \end{eqnarray}
\] で求められます。また，一様磁界中の磁界の大きさ$ \ \boldsymbol H \ \mathrm {[A / m]} \ $，磁束密度が$ \ \boldsymbol B \ \mathrm {[T]} \ $，透磁率が$ \ \mu \ \mathrm {[H / m]} \ $であるとき，磁気エネルギー密度$ \ w_{\mathrm {h}} \ \mathrm {[J / m^{3}]} \ $は，
\[
\begin{eqnarray}
w_{\mathrm {h}} &=&\frac {1}{2}\boldsymbol H\cdot \boldsymbol B \\[ 5pt ] &=&\frac {1}{2}\mu \left| \boldsymbol H\right| ^{2} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)解答：チ
中心軸から$ \ r \ $の内側に流れる電流の大きさ$ \ I_{\mathrm {r}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {r}}&=&\frac {\pi r^{2}}{\pi a^{2}}I \\[ 5pt ] &=&\frac {r^{2}}{a^{2}}I \\[ 5pt ] \end{eqnarray}
\] であるので，磁界の強さ$ \ H_{\mathrm {r}} \ $は，ワンポイント解説「1.アンペア（アンペール）の周回積分の法則」の通り，
\[
\begin{eqnarray}
H_{\mathrm {r}}&=&\frac {I_{\mathrm {r}}}{2\pi r} \\[ 5pt ] &=&\frac {\displaystyle \frac {r^{2}}{a^{2}}I}{2\pi r} \\[ 5pt ] &=&\frac {rI}{2\pi a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヌ
$ \ r \ $における単位体積当たりの磁気エネルギー$ \ w_{\mathrm {m}}\left( r\right) \ $は，ワンポイント解説「6.エネルギー密度$ \ w \ $」の通り，
\[
\begin{eqnarray}
w_{\mathrm {m}}\left( r\right) &=&\frac {1}{2}\mu {H_{\mathrm {r}}}^{2} \\[ 5pt ] &=&\frac {1}{2}\mu \left( \frac {rI}{2\pi a^{2}}\right) ^{2} \\[ 5pt ] &=&\frac {\mu r^{2}I^{2}}{8\pi ^{2}a^{4}} \\[ 5pt ] \end{eqnarray}
\] となるので，題意より磁気エネルギー$ \ W_{\mathrm {i}} \ $は，
\[
\begin{eqnarray}
W_{\mathrm {i}} &=&\int ^{a}_{0} w_{\mathrm {m}}\left( r\right) 2\pi r \mathrm {d}r \\[ 5pt ] &=&\int ^{a}_{0} \frac {\mu r^{2}I^{2}}{8\pi ^{2}a^{4}} 2\pi r \mathrm {d}r \\[ 5pt ] &=&\frac {\mu I^{2}}{4\pi a^{4}}\int ^{a}_{0} r^{3} \mathrm {d}r \\[ 5pt ] &=&\frac {\mu I^{2}}{4\pi a^{4}}\left[ \frac {r^{4}}{4}\right] ^{a}_{0} \\[ 5pt ] &=&\frac {\mu I^{2}}{4\pi a^{4}}\cdot \frac {a^{4}}{4} \\[ 5pt ] &=&\frac {\mu I^{2}}{16\pi } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
円柱導体の単位長さあたりの抵抗$ \ R \ $は，ワンポイント解説「2.導体の抵抗率及び導電率」の通り，
\[
\begin{eqnarray}
R &=&\frac {l}{\sigma S} \\[ 5pt ] &=&\frac {1}{\sigma \pi a^{2}} \\[ 5pt ] \end{eqnarray}
\] となるので，求める電圧$ \ E_{\mathrm {DC}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {DC}} &=&RI \\[ 5pt ] &=&\frac {1}{\sigma \pi a^{2}}\cdot I \\[ 5pt ] &=&\frac {I}{\sigma \pi a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ロ
ワンポイント解説「3.表皮効果」の通り，交流では表皮効果により導体の中心部の電流が流れにくくなり，導体断面積が小さくなったと考えることができるため，導体の抵抗が大きくなります。したがって，$ \ E_{\mathrm {AC}}＞E_{\mathrm {DC}} \ $の関係があります。

(5)解答：ヨ
ワンポイント解説「3.表皮効果」の通り，電流密度分布として正しいのは導体の外側の電流密度が大きい（ヨ）となります。