Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,影像法を用いた静電容量の解析に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,空気の誘電率は\( \ \varepsilon _{0} \ \),大地は完全導体として計算せよ。
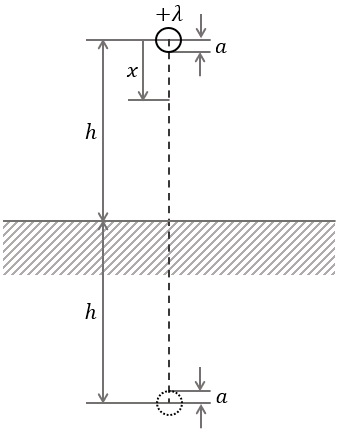
図に示すように,大地面から高さ\( \ h \ \)の位置に大地面と平行に張られた直線状の電線を考える。電線は無限長であり,半径\( \ a \ \)は\( \ h \ \)よりも十分小さい\( \ \left( a≪h \right) \ \)。影像法を用いる場合,大地面から深さ\( \ h \ \)の位置に半径\( \ a \ \)で無限長の影像電線を考え,電線に単位長さ当たり\( \ +\lambda \ \)の電荷を与えると,影像電線の単位長さ当たりの電荷は\( \ \fbox { (1) } \ \)となる。このとき,電線から大地に向かう垂線上で電線の中心軸から距離\( \ x\left( ≧a \right) \ \)の位置に電線の電荷\( \ +\lambda \ \)がつくる電界の強さは\( \ E_{1}\left( x\right)= \ \fbox { (2) } \ \),影像電線の電荷がつくる電界の強さは\( \ E_{2}\left( x\right) = \ \fbox { (3) } \ \)となり,電線の中心軸から距離\( \ x \ \)の位置の電界の強さは\( \ E\left( x\right) =E_{1}\left( x\right) +E_{2}\left( x\right) \ \)と求まる。
\( \ E\left( x\right) \ \)を\( \ a≦ x≦h \ \)の範囲で積分すると,電線と大地面との間の電位差\( \ V \ \)は\( \ \fbox { (4) } \ \)と求まる。これにより,電線と大地面との間の単位長さ当たりの静電容量は\( \ \fbox { (5) } \ \)と求まる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 0 &(ロ)& \frac {\lambda }{2\pi \varepsilon _{0}\left( x-h\right) } &(ハ)& \frac {\lambda }{2\pi \varepsilon _{0}x } \\[ 5pt ]
&(ニ)& \frac {\lambda }{2\pi \varepsilon _{0}\left( x-a \right) } &(ホ)& \frac {\lambda }{2\pi \varepsilon _{0}\left( h-x\right) } &(ヘ)& \frac {4\pi \varepsilon _{0}}{\displaystyle \ln \left( \frac {2h-a}{a}\right) } \\[ 5pt ]
&(ト)& \frac {\lambda }{\pi \varepsilon _{0} }\ln \left( \frac {2h-a}{a}\right) &(チ)& \frac {2\pi \varepsilon _{0}}{\displaystyle \ln \left( \frac {2h-a}{a}\right) } &(リ)& \frac {\lambda }{\pi \varepsilon _{0} }\ln \left( \frac {h-a}{a}\right) \\[ 5pt ]
&(ヌ)& \frac {\lambda }{2\pi \varepsilon _{0}\left( h+x\right) } &(ル)& \frac {\lambda }{2\pi \varepsilon _{0} }\ln \left( \frac {2h-a}{a}\right) &(ヲ)& -\lambda \\[ 5pt ]
&(ワ)& +\lambda &(カ)& \frac {\lambda }{2\pi \varepsilon _{0}\left( 2h-x\right) } &(ヨ)& \frac {\pi \varepsilon _{0}}{\displaystyle \ln \left( \frac {2h-a}{a}\right) } && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電気影像法を用い電線の静電容量の導出する問題です。
電気影像法の分野で出てくる典型的な問題で,電磁気学のテキストであれば演習問題としてほぼ同じ問題が掲載されているような内容です。
難易度が高い問題が出題されやすい\( \ 2 \ \)種の電磁気としては幾分取り組みやすい問題となりますので,ぜひ完答を目指せるようにして下さい。
1.ガウスの法則
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
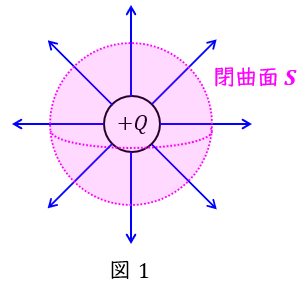
となり,これをガウスの法則といいます。例えば,図1に示すような,点電荷\( \ Q \ \mathrm {[C]} \ \)をおいた場合の距離\( \ r \ \mathrm {[m]} \ \)での電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
4\pi r^{2}E &=& \frac {Q}{\varepsilon } \\[ 5pt ]
E &=& \frac {Q}{4\pi \varepsilon r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 3 \ \)種で学習した公式と同じ公式が導出できます。
また,\( \ 2 \ \)種で出題されやすいのは電荷が蓄えられるのが同軸円筒導体のパターンで,単位長さ当たりに蓄えられている電荷が\( \ q \ \mathrm {[C]} \ \)である場合は,単位長さ当たりの電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
2\pi r \times 1 \cdot E &=& \frac {q}{\varepsilon } \\[ 5pt ]
E &=& \frac {q}{2\pi \varepsilon r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.空間上の電位\( \ V \ \)
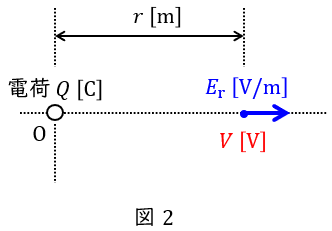
中心からの距離\( \ r \ \mathrm {[m]} \ \)に関する電界\( \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ \)が与えられている時,その場所の電位\( \ V \ \mathrm {[V]} \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
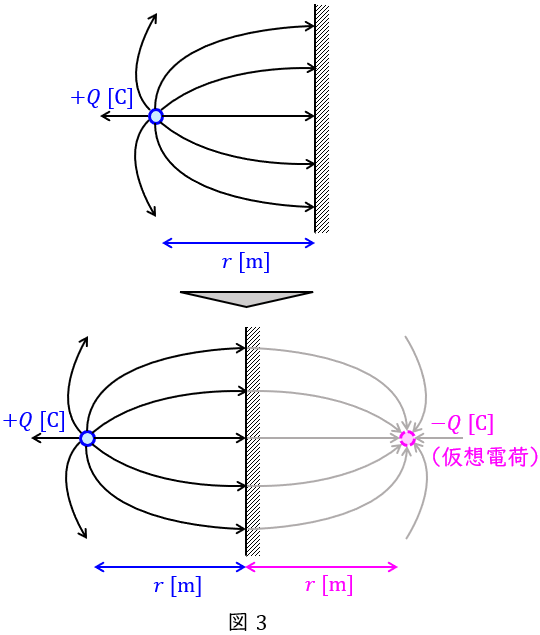
3.電気影像法
図3のような平面導体から距離\( \ r \ \mathrm {[m]} \ \)を隔てて電荷があるとき,電気力線は導体に垂直に入射するため,符号が逆の電荷(仮想電荷)を設定して電界を求めることができます。これを電気影像法といいます。
4.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となった場合,対数を外すと,
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ヲ
ワンポイント解説「3.電気影像法」の通り,電線に単位長さ当たり\( \ +\lambda \ \)の電荷を与えると,影像電線の単位長さ当たりの電荷は\( \ -\lambda \ \)と求められる。
(2)解答:ハ
電線の電荷\( \ +\lambda \ \)と電界の強さ\( \ E_{1}\left( x\right) \ \)の関係は,ワンポイント解説「1.ガウスの法則」の通り,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E_{1} \cdot \mathrm {d}\boldsymbol S &=& \frac {\lambda }{\varepsilon _{0} } \\[ 5pt ]
2\pi x \times 1 \cdot E_{1}\left( x\right) &=& \frac {\lambda }{\varepsilon _{0} } \\[ 5pt ]
E_{1}\left( x\right) &=& \frac {\lambda }{2\pi \varepsilon _{0}x } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:カ
影像電線の電荷\( \ -\lambda \ \)と電界の強さ\( \ E_{2}\left( x\right) \ \)の関係は,ワンポイント解説「1.ガウスの法則」の通り,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E_{2} \cdot \mathrm {d}\boldsymbol S &=& \frac {\lambda }{\varepsilon _{0} } \\[ 5pt ]
2\pi \left( 2h-x\right) \times 1 \cdot E_{2}\left( x\right) &=& \frac {\lambda }{\varepsilon _{0} } \\[ 5pt ]
E_{2}\left( x\right) &=& \frac {\lambda }{2\pi \varepsilon _{0}\left( 2h-x\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
(2)及び(3)解答式より,電線の中心軸から距離\( \ x \ \)の位置の電界の強さは\( \ E\left( x\right) \ \)は,どちらも電界の向きは同じであるから,
\[
\begin{eqnarray}
E\left( x\right) &=& E_{1}\left( x\right) +E_{2}\left( x\right) \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0}x } +\frac {\lambda }{2\pi \varepsilon _{0}\left( 2h-x\right) } \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0} }\left( \frac {1}{x}+\frac {1}{2h-x}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,電線と大地面との間の電位差\( \ V \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V&=&-\int _{h}^{a}E\left( x\right) \mathrm {d}x \\[ 5pt ]
&=&-\int _{h}^{a}\frac {\lambda }{2\pi \varepsilon _{0} }\left( \frac {1}{x}+\frac {1}{2h-x}\right) \mathrm {d}x \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0} }\int _{h}^{a}\left( \frac {1}{x}+\frac {1}{2h-x}\right) \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ 2h-x=t \ \)とすると,\( \ x \ \)の積分範囲が\( \ h \ \)から\( \ a \ \)までであるとき,\( \ t \ \)の積分範囲は\( \ 2h-h=h \ \)から\( \ 2h-a \ \)までとなり,\( \ \displaystyle \frac {\mathrm {d}t}{\mathrm {d}x}=-1 ⇔ \mathrm {d}x=-\mathrm {d}t \ \)であるから,
\[
\begin{eqnarray}
V&=&-\frac {\lambda }{2\pi \varepsilon _{0} }\left\{ \int _{h}^{a} \frac {1}{x}\mathrm {d}x+\int _{h}^{2h-a}\frac {1}{t} \left( -\mathrm {d}t\right) \right\} \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0} }\left( \int _{h}^{a} \frac {1}{x}\mathrm {d}x-\int _{h}^{2h-a}\frac {1}{t} \mathrm {d}t \right) \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0} }\left( \left[ \ln x \right] _{h}^{a}-\left[ \ln t \right] _{h}^{2h-a} \right) \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0} }\left\{ \ln a-\ln h -\ln \left( 2h-a \right) +\ln h \right\} \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0} }\left\{ \ln a -\ln \left( 2h-a \right) \right\} \\[ 5pt ]
&=&\frac {\lambda }{2\pi \varepsilon _{0} }\left\{ \ln \left( 2h-a \right) -\ln a \right\} \\[ 5pt ]
&=&\frac {\lambda }{2\pi \varepsilon _{0} }\ln \left( \frac {2h-a}{a}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:チ
(4)解答式を変形すると,電線と大地面との間の単位長さ当たりの静電容量\( \ C \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\lambda }{2\pi \varepsilon _{0} }\ln \left( \frac {2h-a}{a}\right) \\[ 5pt ]
\frac {\lambda }{V}&=&\frac {2\pi \varepsilon _{0}}{\displaystyle \ln \left( \frac {2h-a}{a}\right) } \\[ 5pt ]
C&=&\frac {2\pi \varepsilon _{0}}{\displaystyle \ln \left( \frac {2h-a}{a}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは