《理論》〈電気回路〉[R07:問3]素子を組み合わせた回路の電力が最大となる条件に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，交流電気回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

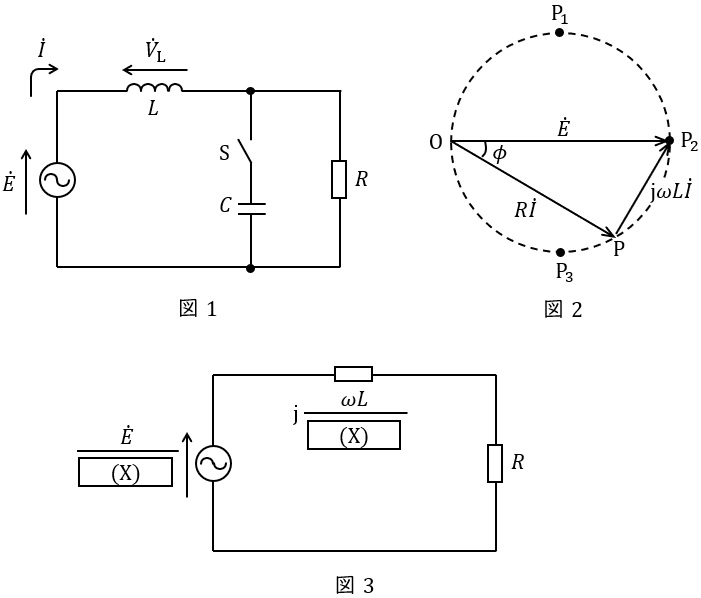
起電力$ \ \dot E=E\mathrm {e}^{\mathrm {j}0} \ $で角周波数$ \ \omega \ $の交流電圧源から，インダクタンス$ \ L \ $を持つ電線を介して抵抗$ \ R \ $の負荷に電力を送る図1の回路がある。$ \ R \ $を変化させるとき，電力が最大となる条件を求めたい。ただし，静電容量$ \ C \ $を持つコンデンサがあって，必要に応じて負荷に並列に接続できるものとし，$ \ \dot E \ $と，ここから流れ出る電流$ \ \dot I \ $の位相差を$ \ \phi \ $とする。また，$ \ \omega ^{2}LC ＜ 1 \ $が成立するものとする。

スイッチ$ \ \mathrm {S} \ $が開のときの回路の電圧ベクトル図を図2に示す。$ \ R \ $を変化させると電流の変化につれて三角形$ \ \mathrm {OP_{2}P} \ $も変化するが，$ \ R\dot I \ $と$ \ {\dot V}_{\mathrm {L}}=\mathrm {j}\omega L\dot I \ $は直交するので直角の頂点$ \ \mathrm {P} \ $は$ \ \dot E \ $を直径とする円周上を移動する。

$ \ {\dot V}_{\mathrm {L}} \ $は$ \ R \ $を変化させても常に電流に比例する長さを持ち$ \ V_{\mathrm {L}}=k I \ $と書ける（$ \ k= \omega L \ $は比例係数）が，一方，$ \ {\dot V}_{\mathrm {L}} \ $と$ \ \dot E \ $との位相差は$ \ \fbox {　（１）　} \ $であるから三角形$ \ \mathrm {OP_{2}P} \ $の面積は$ \ \displaystyle \frac {1}{2} EV_{\mathrm {L}} \ \fbox {　（２）　} \ =\frac {1}{2} EV_{\mathrm {L}} \cos \phi =\frac {1}{2} kEI \cos \phi \ $と書ける。この式の右辺は電力$ \ EI \cos \phi \ $に比例することから，電力の大きさは三角形$ \ \mathrm {OP_{2}P} \ $の面積に比例することが分かる。したがって，電力が最大となるのは，頂点$ \ \mathrm {P} \ $が点$ \ \fbox {　（３）　} \ $に一致したときであり，その条件は$ \ \fbox {　（４）　} \ $である。

一方，$ \ \mathrm {S} \ $を閉じてコンデンサを接続すると回路は図3の等価回路で表すことができ，図3の$ \ 2 \ $箇所の$ \ \fbox {　（X）　} \ $に入る数式は$ \ \fbox {　（５）　} \ $である。このときの電力を計算すると，$ \ \displaystyle \frac {RE^{2}}{R^{2}\left( 1-\omega ^{2}LC\right) ^{2}+\omega ^{2}L^{2}} \ $となり，コンデンサを入れることで電力は増加する。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\mathrm {P_{1}}　　　　&（ロ）&　\mathrm {P_{2}}　　　　　&（ハ）&　\mathrm {P_{3}} \\[ 5pt ] &（ニ）&　\phi　　　　　&（ホ）&　1-\omega CR　　　　&（ヘ）&　\omega LR=1 \\[ 5pt ] &（ト）&　\sin \left( \frac {\pi }{2}-\phi \right) 　　　　&（チ）&　\omega ^{2}LR=1　　　　　&（リ）&　1-\omega ^{2}LC \\[ 5pt ] &（ヌ）&　R=\omega L　　　　　&（ル）&　\tan \left( \frac {\pi }{2}-\phi \right) 　　　　&（ヲ）&　\pi -\phi \\[ 5pt ] &（ワ）&　\cos \left( \frac {\pi }{2}-\phi \right)　　　　&（カ）&　1+\frac {1}{\omega CR}　　　　　&（ヨ）&　\frac {\pi }{2}-\phi \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

抵抗，インダクタンス，コンデンサを組み合わせた回路の電力が最大となる条件や回路変形を考える問題です。
問題の誘導に従い解いていく必要がある$ \ 2 \ $種らしい問題ですが，計算量はそれほど多くないため，問題文の長さに惑わされずに落ち着いていけば高得点を狙うことができます。

1.抵抗，コイル，コンデンサの電圧$ \ V \ \mathrm {[V]} \ $と電流$ \ I \ \mathrm {[A]} \ $の関係
抵抗$ \ R \ \mathrm {[\Omega ]} \ $，コイル$ \ L \ \mathrm {[H]} \ $，コンデンサ$ \ C \ \mathrm {[F]} \ $があり，電源の角周波数$ \ \omega \ \mathrm {[rad / s]} \ $及び周波数$ \ f \ \mathrm {[Hz]} \ $が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
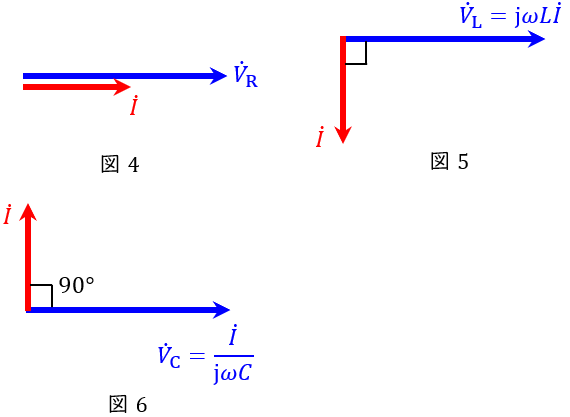
\] となります。この関係をベクトル図に表すと，図4～図6となります。

2.テブナンの定理
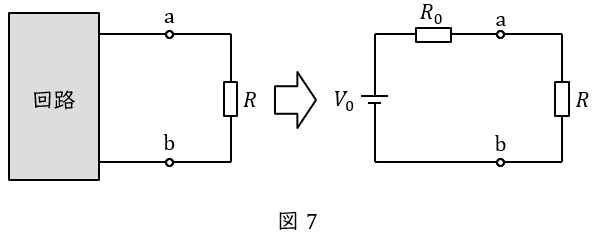
図7のように複雑な回路を電圧源$ \ V_{0} \ \mathrm {[V]} \ $と抵抗$ \ R_{0} \ \mathrm {[\Omega ]} \ $に置き換える方法です。
$ \ V_{0} \ \mathrm {[V]} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $の開放電圧，$ \ R_{0} \ \mathrm {[\Omega ]} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $から電源側回路を見た合成抵抗となります。
ただし，$ \ R_{0} \ \mathrm {[\Omega ]} \ $を求める際，電圧源は短絡，電流源は開放します。

※一般に直流回路で学習する項目ですが，本問のような交流回路においても適用可能です。

【解答】

(1)解答：ヨ
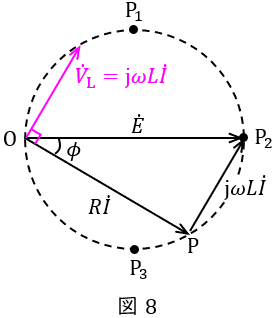
$ \ {\dot V}_{\mathrm {L}} \ $を点$ \ \mathrm {O} \ $からのベクトルに平行移動すると，図8に示すようになる。よって，$ \ {\dot V}_{\mathrm {L}} \ $と$ \ \dot E \ $との位相差は$ \ \displaystyle \frac {\pi }{2}-\phi \ $と求められる。

(2)解答：ト
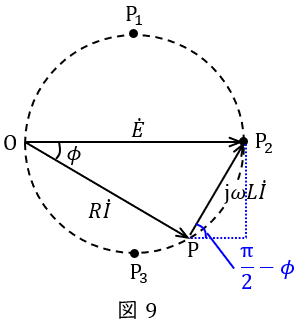
図9に示すように，$ \ \dot E \ $を底辺としたときの三角形$ \ \mathrm {OP_{2}P} \ $の高さは$ \ \displaystyle V_{\mathrm {L}}\sin \left( \frac {\pi }{2}-\phi \right) \ $となるので，三角形$ \ \mathrm {OP_{2}P} \ $の面積は，
\[
\begin{eqnarray}
&\frac {1}{2} EV_{\mathrm {L}} \sin \left( \frac {\pi }{2}-\phi \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
題意より，電力の大きさは三角形$ \ \mathrm {OP_{2}P} \ $の面積に比例するので，電力が最大となるのは$ \ \dot E \ $を底辺としたときの高さが最大となる頂点$ \ \mathrm {P_{3}} \ $と求められる。

(4)解答：ヌ
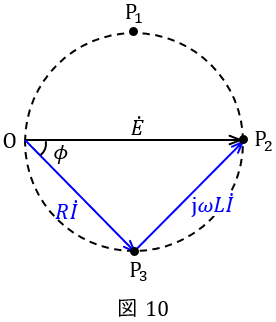
図10に示すように，頂点$ \ \mathrm {P} \ $が$ \ \mathrm {P_{3}} \ $のとき$ \ R\dot I \ $と$ \ \mathrm {j}\omega L\dot I \ $の大きさは等しいので，
\[
\begin{eqnarray}
RI&=&\omega L I \\[ 5pt ] R&=&\omega L \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：リ
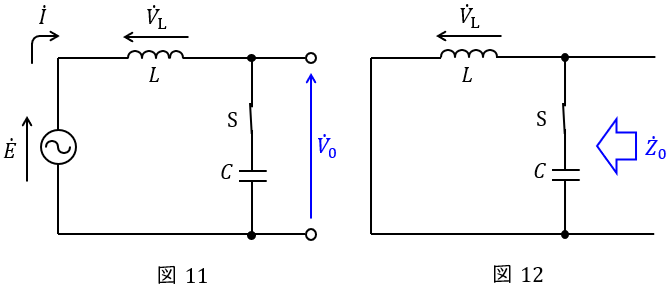
図1の回路にテブナンの定理を適用すると，開放電圧$ \ {\dot V}_{0} \ $は，図11より，
\[
\begin{eqnarray}
{\dot V}_{0}&=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{\mathrm {j}\omega L+\displaystyle \frac {1}{\mathrm {j}\omega C}}\dot E \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{\mathrm {j}\omega L+\displaystyle \frac {1}{\mathrm {j}\omega C}}\times \frac {\mathrm {j}\omega C}{\mathrm {j}\omega C}\dot E \\[ 5pt ] &=&\frac {1}{-\omega ^{2}LC+1}\dot E \\[ 5pt ] &=&\frac {\dot E}{1-\omega ^{2}LC} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ R \ $を切り離したときの電源側を見た合成インピーダンス$ \ {\dot Z}_{0} \ $は，図12より，
\[
\begin{eqnarray}
{\dot Z}_{0}&=&\frac {\displaystyle \mathrm {j}\omega L\cdot \frac {1}{\mathrm {j}\omega C}}{\mathrm {j}\omega L+\displaystyle \frac {1}{\mathrm {j}\omega C}} \\[ 5pt ] &=&\frac {\displaystyle \frac {\mathrm {j}\omega L}{\mathrm {j}\omega C}}{\mathrm {j}\omega L+\displaystyle \frac {1}{\mathrm {j}\omega C}}\times \frac {\mathrm {j}\omega C}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {\mathrm {j}\omega L}{-\omega ^{2}LC+1} \\[ 5pt ] &=&\mathrm {j}\frac {\omega L}{1-\omega ^{2}LC} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ \fbox {　（X）　} \ $に入る数式は$ \ 1-\omega ^{2}LC \ $と求められる。