Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,エミッタ接地増幅回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
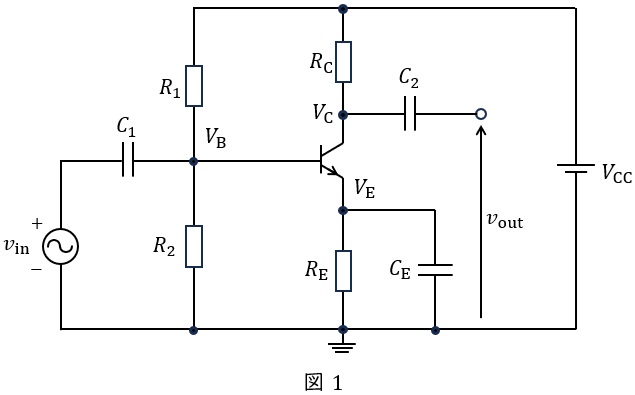
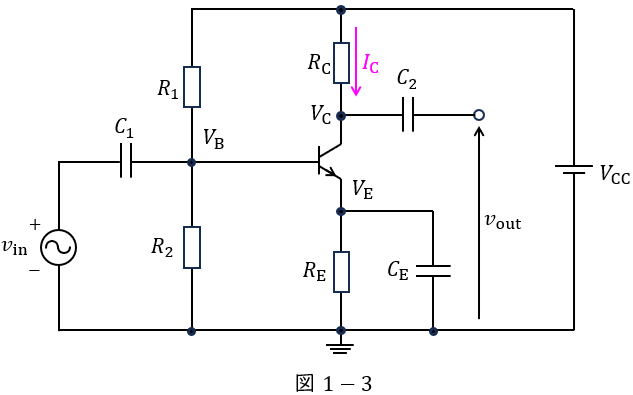
まず,入力電圧\( \ v_{\mathrm {in}}=0 \ \)とし,図1のエミッタ接地増幅回路の各部のバイアス電位及び電流を求める。ただし,回路の電源電圧は\( \ V_{\mathrm {CC}} \ \)とし,各抵抗器の抵抗値は\( \ R_{\mathrm {1}} \ \),\( \ R_{\mathrm {2}} \ \),\( \ R_{\mathrm {E}} \ \),\( \ R_{\mathrm {C}} \ \)とする。ベースを流れるバイアス電流\( \ I_{\mathrm {B}} \ \)が他の電流に比べ小さく無視できるとき,ベース電位\( \ V_{\mathrm {B}} \ \)は\( \ \fbox { (1) } \ \)となる。このとき,エミッタ電流\( \ I_{\mathrm {E}} \ \)は,\( \ V_{\mathrm {B}} \ \)とベースーエミッタ間電圧\( \ V_{\mathrm {BE}} \ \)を用いて\( \ \fbox { (2) } \ \)となる。一方,コレクタ電位\( \ V_{\mathrm {C}} \ \)は,コレクタ電流\( \ I_{\mathrm {C}} \ \)を用いて\( \ \fbox { (3) } \ \)となる。エミッタ電流とコレクタ電流が等しいとみなせるとき,\( \ \fbox { (2) } \ \)と\( \ \fbox { (3) } \ \)から\( \ V_{\mathrm {C}} \ \)が求まる。
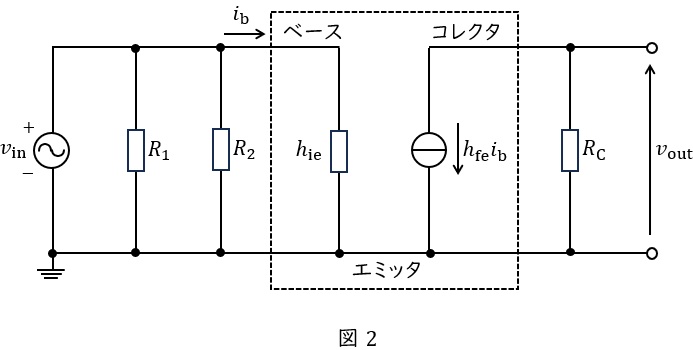
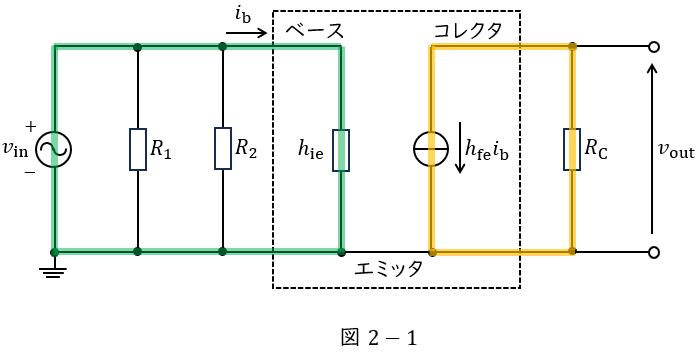
次に,図1のエミッタ接地増幅回路の電圧増幅度を求める。各コンデンサの静電容量は\( \ C_{\mathrm {1}} \ \),\( \ C_{\mathrm {2}} \ \),\( \ C_{\mathrm {E}} \ \)であり,信号の周波数において,全てのコンデンサのインピーダンスは小さく無視できるとする。このとき,図1の交流等価回路は図2となる。図2において破線で囲まれた部分はトランジスタの交流等価回路であり,\( \ h_{\mathrm {ie}} \ \)と\( \ h_{\mathrm {fe}} \ \)はそれぞれ用いたトランジスタの入力インピーダンスと電流増幅率である。入力電圧\( \ v_{\mathrm {in}} \ \)を加えた際の出力電圧は\( \ v_{\mathrm {out}} \ \)より,電圧増幅度\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は\( \ \fbox { (4) } \ \)となる。電圧増幅度の符号から,エミッタ接地増幅回路は\( \ \fbox { (5) } \ \)であることが分かる。
〔問8の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{2}}{R_{1}+R_{2}}V_{\mathrm {CC}} &(ロ)& 非反転増幅回路 &(ハ)& V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ]
&(ニ)& \frac {h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}} &(ホ)& \frac {V_{\mathrm {B}}-V_{\mathrm {BE}}}{R_{\mathrm {E}}+R_{\mathrm {C}}} &(ヘ)& \frac {R_{1}}{R_{1}+R_{2}}V_{\mathrm {CC}} \\[ 5pt ]
&(ト)& \frac {V_{\mathrm {B}}+V_{\mathrm {BE}}}{R_{\mathrm {E}}} &(チ)& エミッタフォロワ &(リ)& \frac {\left( 1+h_{\mathrm {fe}}\right) R_{\mathrm {C}}}{h_{\mathrm {ie}}+\left( 1+h_{\mathrm {fe}}\right) R_{\mathrm {C}}} \\[ 5pt ]
&(ヌ)& \frac {V_{\mathrm {CC}}}{2} &(ル)& R_{\mathrm {C}}I_{\mathrm {C}} &(ヲ)& V_{\mathrm {CC}}-R_{\mathrm {1}}I_{\mathrm {B}} \\[ 5pt ]
&(ワ)& \frac {V_{\mathrm {B}}-V_{\mathrm {BE}}}{R_{\mathrm {E}}} &(カ)& 反転増幅回路 &(ヨ)& -\frac {h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電流帰還バイアス回路を用いたエミッタ接地増幅回路の回路演算に関する問題です。
キルヒホッフの法則や分圧の法則等の基本公式以外の特別な公式は使用しない問題で,解法がポイントなります。ある程度パターン化されていますので,ぜひ得点源とできるようにしましょう。
【解答】
(1)解答:イ
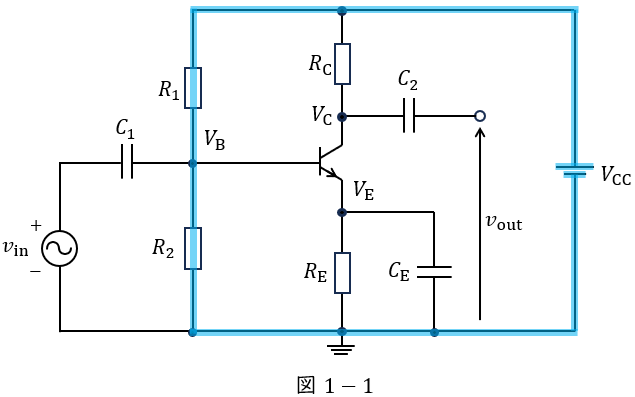
図1-1に示す閉回路に分圧の法則を適用すると,ベース電位\( \ V_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&\frac {R_{2}}{R_{1}+R_{2}}V_{\mathrm {CC}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
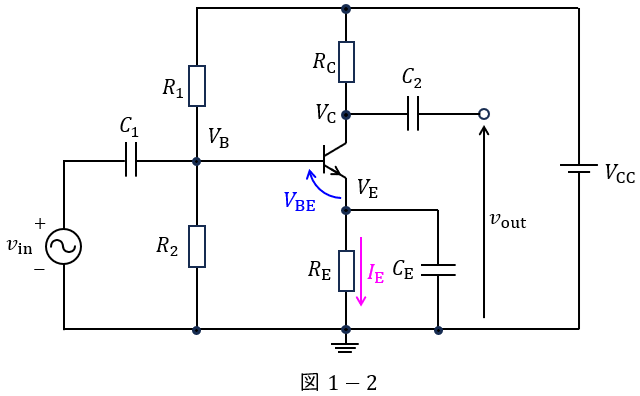
エミッタ電流\( \ I_{\mathrm {E}} \ \)及びベースーエミッタ間電圧\( \ V_{\mathrm {BE}} \ \)は図1-2に示す通りである。
エミッタ電位\( \ V_{\mathrm {E}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {E}}&=&V_{\mathrm {B}}-V_{\mathrm {BE}} \\[ 5pt ]
\end{eqnarray}
\]
であるため,エミッタ電流\( \ I_{\mathrm {E}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {E}}&=&\frac {V_{\mathrm {E}}}{R_{\mathrm {E}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {B}}-V_{\mathrm {BE}}}{R_{\mathrm {E}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ハ
コレクタ電流\( \ I_{\mathrm {C}} \ \)は図1-3に示す電流であるので,コレクタ電位\( \ V_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {C}}&=&V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
図2-1に示す左側の閉回路において,
\[
\begin{eqnarray}
i_{\mathrm {b}}&=&\frac {v_{\mathrm {in}}}{h_{\mathrm {ie}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,これと右側の閉回路より,
\[
\begin{eqnarray}
v_{\mathrm {out}}&=&-R_{\mathrm {C}}h_{\mathrm {fe}}i_{\mathrm {b}} \\[ 5pt ]
&=&-R_{\mathrm {C}}h_{\mathrm {fe}}\cdot \frac {v_{\mathrm {in}}}{h_{\mathrm {ie}}} \\[ 5pt ]
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&-\frac {h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
電圧増幅度の符号がマイナスなので,エミッタ接地増幅回路は反転増幅回路となります。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは