《理論》〈電子理論〉[R01:問8]演算増幅器を用いた回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，演算増幅器を用いた回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。ただし，演算増幅器は理想的であるとする。

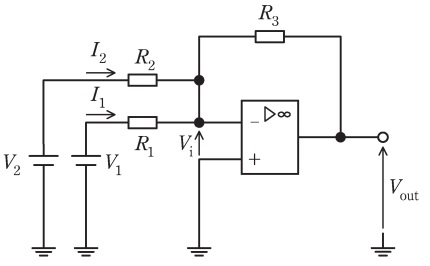
図の回路において演算増幅器の入力端子間の電圧を$ \ V_{\mathrm {i}} \ $とすると，演算増幅器の電圧増幅度が無限大であるとき$ \ V_{\mathrm {i}} \ $は$ \ \fbox {　（１）　} \ $となる。これより，抵抗$ \ R_{1} \ $を流れる電流$ \ I_{1} \ $は，$ \ I_{1}= \ \fbox {　（２）　} \ $と求められる。演算増幅器の入力端子には電流が流れないことから，抵抗$ \ R_{1} \ $を流れる電流$ \ I_{1} \ $と抵抗$ \ R_{2} \ $を流れる電流$ \ I_{2} \ $は抵抗$ \ R_{3} \ $を流れる。この結果，$ \ R_{3} \ $の両端には大きさが$ \ \fbox {　（３）　} \ $の電圧が現れる。$ \ R_{1}=R_{2}=R_{3}=R \ $とすると，出力電圧は$ \ V_{\mathrm {out}}= \ \fbox {　（４）　} \ $となる。この出力電圧より，この回路は$ \ \fbox {　（５）　} \ $と呼ばれる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {V_{1}}{R_{1}}　　　&（ロ）&　-\left( V_{1}+V_{2}\right)　　　&（ハ）&　1 \\[ 5pt ] &（ニ）&　R_{3}\left( I_{1}-I_{2}\right)　　　&（ホ）&　R_{3}I_{1}I_{2}　　　&（ヘ）&　\frac {R_{1}}{V_{1}} \\[ 5pt ] &（ト）&　R_{3}\left( I_{1}+I_{2}\right)　　　&（チ）&　積分回路　　　&（リ）&　-V_{1}V_{2} \\[ 5pt ] &（ヌ）&　乗算回路　　　&（ル）&　\frac {V_{1}}{R_{1}+R_{3}}　　　&（ヲ）&　加算回路 \\[ 5pt ] &（ワ）&　-\left( V_{1}-V_{2}\right)　　　&（カ）&　無限大　　　&（ヨ）&　0 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

演算増幅器を使用した電子回路に関する問題です。基本的な演算増幅器の特徴を理解していれば難なく解ける問題であると思います。

1.理想的な演算増幅器の特徴
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は$ \ 0 \ \mathrm {V} \ $(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

【解答】

(1)解答：ヨ
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，入力端子間の電圧差は$ \ 0 \ \mathrm {V} \ $であるので，$ \ V_{\mathrm {i}}=0 \ \mathrm {V} \ $である。

(2)解答：イ
演算増幅器のマイナスの入力が$ \ 0 \ \mathrm {V} \ $であるので，抵抗$ \ R_{1} \ $には電圧$ \ V_{1} \ $がかかる。したがって，
\[
\begin{eqnarray}
I_{1} &=&\frac {V_{1}}{R_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
抵抗$ \ R_{2} \ $に流れる電流も(2)と同様に求めると，演算増幅器のマイナスの入力が$ \ 0 \ \mathrm {V} \ $であるので，抵抗$ \ R_{2} \ $には電圧$ \ V_{2} \ $がかかる。したがって，
\[
\begin{eqnarray}
I_{2} &=&\frac {V_{2}}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，演算増幅器には電流が流れないので，$ \ R_{3} \ $には$ \ I_{1}+I_{2} \ $の電流が流れる。したがって，$ \ R_{3} \ $の両端には，$ \ R_{3}\left( I_{1}+I_{2}\right) \ $の電圧が現れる。

(4)解答：ロ
(3)より，出力電圧$ \ V_{\mathrm {out}} \ $は，電流の向きに注意すると，
\[
\begin{eqnarray}
V_{\mathrm {out}} &=&-R_{3}\left( I_{1}+I_{2}\right) \\[ 5pt ] &=&-R_{3}\left( I_{1}+I_{2}\right) \\[ 5pt ] &=&-R_{3}\left( \frac {V_{1}}{R_{1}}+\frac {V_{2}}{R_{2}}\right) \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$ \ R_{1}=R_{2}=R_{3}=R \ $を代入すると，
\[
\begin{eqnarray}
V_{\mathrm {out}} &=&-R\left( \frac {V_{1}}{R}+\frac {V_{2}}{R}\right) \\[ 5pt ] &=&-\left( V_{1}+V_{2}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
符号が逆になりますが，出力電圧が入力電圧の和になるので，この回路は加算回路と呼ばれます。