《電力》〈配電〉[R07上:問13]力率変化に伴う配電線の負荷電力の変化に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

三相\( \ 3 \ \)線式配電線により遅れ力率\( \ 70 \ \mathrm {％} \ \)，\( \ W_{1} \ \mathrm {[kW]} \ \)の負荷に電力を供給している。負荷が遅れ力率\( \ 91 \ \mathrm {％} \ \)，\( \ W_{2} \ \mathrm {[kW]} \ \)に変化したが線路損失は変わらなかった。\( \ W_{2} \ \)は\( \ W_{1} \ \)の何倍か。最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，負荷の端子電圧は変わらないものとする。

　(1)　\( \ 0.77 \ \)　　(2)　\( \ 1.3 \ \)　　(3)　\( \ 2.3 \ \)　　(4)　\( \ 1.1 \ \)　　(5)　\( \ 1.7 \ \)

【ワンポイント解説】

三相\( \ 3 \ \)線式配電線の力率変化による負荷電力の変化に関する問題です。
重要公式である電力の公式\( \ P =\sqrt {3}V_{\mathrm {r}}I\cos \theta \ \)と電力損失\( \ P_{\mathrm {L}} =3rI^{2} \ \)を組み合わせて導出します。
本問は平成8年問9からの再出題となります

1.送電線の送電電力と電力損失
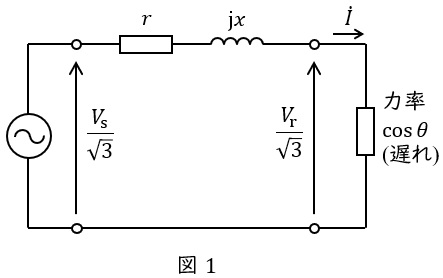
送電端の電圧が\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)，受電端の電圧が\( \ V_{\mathrm {r}} \ \mathrm {[V]} \ \)，送電線の\( \ 1 \ \)線あたりの抵抗が\( \ r \ \mathrm {[\Omega ]} \ \)，リアクタンスが\( \ x \ \mathrm {[\Omega ]} \ \)，送電線に流れる電流が\( \ I \ \mathrm {[A]} \ \)，負荷の力率が\( \ \cos \theta \ \)であるとすると，送電線の一相分等価回路は図1のように描くことができます。

このとき，負荷電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&\sqrt {3}V_{\mathrm {r}}I\cos \theta \\[ 5pt ] \end{eqnarray}
\] となり，上式より，
\[
\begin{eqnarray}
I &=&\frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta } \\[ 5pt ] \end{eqnarray}
\] であるため，送電線での電力損失\( \ P_{\mathrm {L}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {L}} &=&3rI^{2} \\[ 5pt ] &=&3r\left( \frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta }\right) ^{2} \\[ 5pt ] &=&\frac {P^{2}r}{V_{\mathrm {r}}^{2}\cos ^{2}\theta } \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
ワンポイント解説「1.送電線の送電電力と電力損失」の通り，電力損失\( \ P_{\mathrm {L}} \ \mathrm {[W]} \ \)が一定であるとき，
\[
\begin{eqnarray}
P_{\mathrm {L}} &=&\frac {P^{2}r}{V_{\mathrm {r}}^{2}\cos ^{2}\theta } \\[ 5pt ] P^{2}r&=&P_{\mathrm {L}}V_{\mathrm {r}}^{2}\cos ^{2}\theta \\[ 5pt ] P^{2}&=&\frac {P_{\mathrm {L}}V_{\mathrm {r}}^{2}}{r}\cos ^{2}\theta \\[ 5pt ] P&=&\sqrt {\frac {P_{\mathrm {L}}V_{\mathrm {r}}^{2}}{r}}\cos \theta \\[ 5pt ] \end{eqnarray}
\] となり，負荷電力\( \ P \ \mathrm {[W]} \ \)は力率\( \ \cos \theta \ \)に比例することがわかる。よって，力率\( \ \cos \theta _{1}= 0.7 \ \)，\( \ W_{1} \ \mathrm {[kW]} \ \)から力率\( \ \cos \theta _{2}= 0.91 \ \)，\( \ W_{2} \ \mathrm {[kW]} \ \)に変化した場合の関係は，
\[
\begin{eqnarray}
\frac {W_{2}}{W_{1}} &=&\frac {\cos \theta _{2}}{\cos \theta _{1}} \\[ 5pt ] &=&\frac {0.91}{0.7} \\[ 5pt ] &=&1.3 \\[ 5pt ] \end{eqnarray}
\] と求められる。