Contents
【問題】
【難易度】★★★☆☆(普通)
自家用水力発電所を有し,電力系統(電力会社)と常時系統連系(逆潮流ができるものとする。)している工場がある。この工場のある一日の負荷は,図のように変化した。
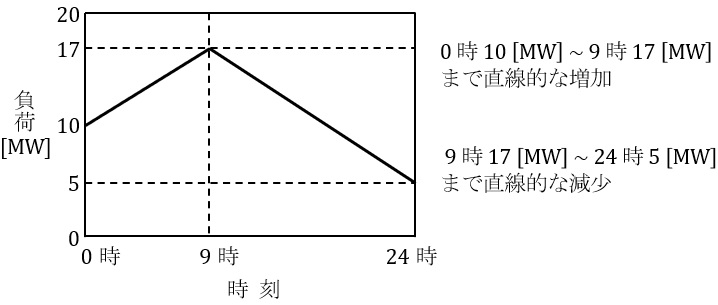
この日の水力発電所の出力は\( \ 10 \ \mathrm {[MW]} \ \)一定であった。次の(a)及び(b)に答えよ。
ただし,水力発電所の所内電力は無視できるものとする。
(a) この日の電力系統からの受電電力量\( \ \mathrm {[MW\cdot h]} \ \)の値として,最も近いのは次のうちどれか。
(1) \( \ 45.4 \ \) (2) \( \ 58.6 \ \) (3) \( \ 62.1 \ \) (4) \( \ 65.6 \ \) (5) \( \ 70.7 \ \)
(b) この日の受電電力量\( \ \mathrm {[MW\cdot h]} \ \left( \mathrm {A}\right) \ \)に対して送電電力量\( \ \mathrm {[MW\cdot h]} \ \left( \mathrm {B}\right) \ \)の比率\( \ \displaystyle \left( \frac {\mathrm {B}}{\mathrm {A}}\right) \ \)として,最も近いのは次のうちどれか。
(1) \( \ 0.20 \ \) (2) \( \ 0.22 \ \) (3) \( \ 0.23 \ \) (4) \( \ 0.25 \ \) (5) \( \ 0.28 \ \)
【ワンポイント解説】
系統に接続している水力発電所の運用に関する問題です。
特別な公式は必要なく,考え方が重要となる問題なので,この問題でテクニックを身につけるようにしましょう。
問題に与えられている図に内容を追記して求めていくのがコツかと思います。
【解答】
(a)解答:(3)
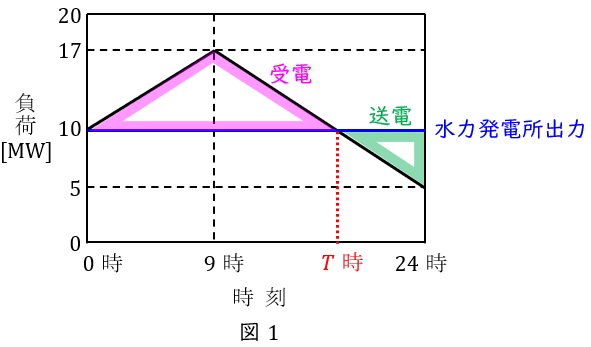
題意に沿って,水力発電所の出力\( \ 10 \ \mathrm {[MW]} \ \),受電している領域,送電している領域を示すと図1のようになる。
\( \ 9 \ \)時から\( \ 24 \ \)時までの負荷特性の直線を一次関数\( \ P=at+b \ \)とおくと,\( \ t=9 \ \mathrm {[時]} \ \)のとき\( \ P=17 \ \mathrm {[MW]} \ \),\( \ t=24 \ \mathrm {[時]} \ \)のとき\( \ P=5 \ \mathrm {[MW]} \ \)であるから,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
17 &=& 9a+b &・・・・・・・・ ①& \\
5 &=& 24a+b &・・・・・・・・ ②& \\
\end{array}
\right.
\end{eqnarray}
\]
の関係があることがわかる。\( \ ②-① \ \)より,
\[
\begin{eqnarray}
-12&=&15a \\[ 5pt ]
a&=&-0.8 \\[ 5pt ]
\end{eqnarray}
\]
となり,これを\( \ ① \ \)に代入すれば,
\[
\begin{eqnarray}
17 &=& 9\times \left( -0.8\right)+b \\[ 5pt ]
17 &=& -7.2+b \\[ 5pt ]
b &=& 24.2 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 9 \ \)時から\( \ 24 \ \)時までの負荷特性は\( \ P=-0.8t+24.2 \ \)と求められる。
これより送電と受電が切り替わる時刻\( \ T \ \)を求めると,
\[
\begin{eqnarray}
10 &=& -0.8T+24.2 \\[ 5pt ]
0.8T &=&14.2 \\[ 5pt ]
T &=& 17.75 \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,受電電力量\( \ W_{\mathrm {r}} \ \mathrm {[MW\cdot h]} \ \)は,図1の三角形の面積を求めれば良いので,
\[
\begin{eqnarray}
W_{\mathrm {r}} &=& \frac {\left( 17.75-0\right) \times \left( 17-10\right) }{2} \\[ 5pt ]
&=& 62.125 → 62.1 \ \mathrm {[MW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
(a)と同様に,送電電力量\( \ W_{\mathrm {s}} \ \mathrm {[MW\cdot h]} \ \)を求めると,
\[
\begin{eqnarray}
W_{\mathrm {s}} &=& \frac {\left( 24-17.75\right) \times \left( 10-5\right) }{2} \\[ 5pt ]
&=& 15.625 \ \mathrm {[MW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,受電電力量\( \ W_{\mathrm {r}} \ \mathrm {[MW\cdot h]} \ \)に対する送電電力量\( \ W_{\mathrm {s}} \ \mathrm {[MW\cdot h]} \ \)の比率は,
\[
\begin{eqnarray}
\frac {W_{\mathrm {s}}}{W_{\mathrm {r}}} &=& \frac {15.625}{62.125} \\[ 5pt ]
&≒& 0.25 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは