《機械》〈同期機〉[R06下:問15]三相同期発電機の同期インピーダンスと発電機出力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格電圧\( \ 6 \ 600 \ \mathrm {V} \ \)，定格出力\( \ 8 \ \mathrm {MV\cdot A} \ \)の三相同期発電機がある。この三相同期発電機において，界磁電流が\( \ 200 \ \mathrm {A} \ \)における無負荷端子電圧は\( \ 6 \ 600 \ \mathrm {V} \ \)であり，この界磁電流での三相短絡電流は\( \ 800 \ \mathrm {A} \ \)であった。この三相同期発電機について，次の(a)及び(b)の問に答えよ。なお，この三相同期発電機の突極性は無視し，電機子巻線抵抗及び鉄損と機械損は十分小さく，計算上は無視できるものとする。

(a)　この三相同期発電機における一相分の同期インピーダンス\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 2.75 \ \)　　(2)　\( \ 4.76 \ \)　　(3)　\( \ 8.25 \ \)　　(4)　\( \ 19.1 \ \)　　(5)　\( \ 33.0 \ \)

(b)　この三相同期発電機を端子電圧\( \ 6 \ 600 \ \mathrm {V} \ \)，力率\( \ 1.0 \ \)で運転したところ，負荷角は\( \ 30° \ \)であった。このときの発電機の出力\( \ \mathrm {[MW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.76 \ \)　　(2)　\( \ 3.05 \ \)　　(3)　\( \ 5.28 \ \)　　(4)　\( \ 6.08 \ \)　　(5)　\( \ 15.9 \ \)

【ワンポイント解説】

同期発電機の同期インピーダンスと発電機出力を求める問題です。
解法手順は短いですが，恐らく多くの受験生が(a)の導出で\( \ \sqrt {3} \ \)で割ることを忘れ，そのまま(b)も間違えてしまったことが予想されます。
同期発電機の等価回路は相電圧であることは必ず理解しておいて下さい。

1.同期発電機の等価回路
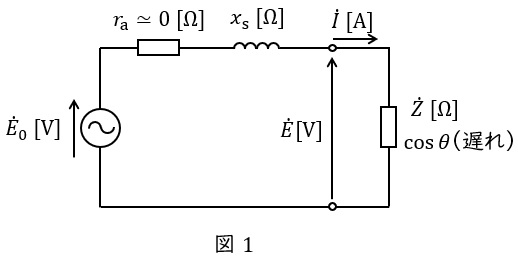
同期発電機の一相分等価回路は誘導起電力（相電圧）\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)，端子電圧（相電圧）\( \ \dot E \ \mathrm {[V]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。
通常，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は十分に小さいと考え，無視して考えることが一般的です。
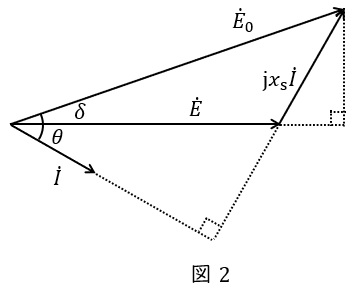
また，等価回路よりベクトル図は図2のようになります。ただし，\( \ \theta \ \)は力率角，\( \ \delta \ \)は負荷角です。

2.同期発電機の出力
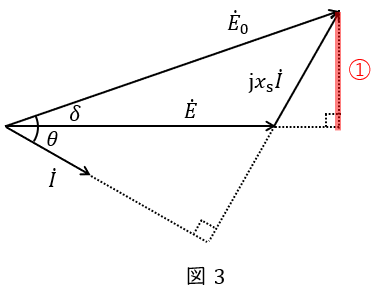
同期発電機のベクトル図は誘導起電力（相電圧）\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)，端子電圧（相電圧）\( \ \dot E \ \mathrm {[V]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)，力率角\( \ \theta \ \)，負荷角\( \ \delta \ \)とすると図3のようになり，このベクトル図において，①線を求める式より，
\[
\begin{eqnarray}
E_{0}\sin \delta &=&x_{\mathrm {s}}I \cos \theta \\[ 5pt ] I \cos \theta &=&\frac {E_{0}\sin \delta }{x_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] であり，三相同期発電機の出力は\( \ P=3EI\cos \theta \ \mathrm {[W]} \ \)で求められるので，これに上式を代入すると，
\[
\begin{eqnarray}
P &=&3EI\cos \theta \\[ 5pt ] &=&\frac {3E_{0}E\sin \delta }{x_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となります。この\( \ 2 \ \)式はどちらも公式として覚えておきましょう。

【解答】

(a)解答：(2)
無負荷端子電圧\( \ \displaystyle E_{0}=\frac {6 \ 600}{\sqrt {3}} \ \mathrm {[V]} \ \)のとき，三相短絡電流\( \ I_{\mathrm {s}}=800 \ \mathrm {[A]} \ \)であるから，一相分の同期インピーダンス（リアクタンス）\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
x_{\mathrm {s}} &=&\frac {E_{0}}{I_{\mathrm {s}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {6 \ 600}{\sqrt {3}}}{800} \\[ 5pt ] &≒&4.763　→　4.76 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
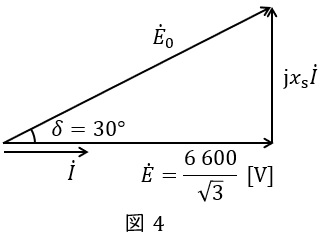
端子電圧\( \ \displaystyle E=\frac {6 \ 600}{\sqrt {3}} \ \mathrm {[V]} \ \)，力率\( \ \cos \theta =1.0 \ \)，負荷角\( \ \delta =30 \ \mathrm {[°]} \ \)であるから，ベクトル図を描くと図4のようになる。
図4より，無負荷誘導起電力の大きさ\( \ E_{0} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E_{0} &=&\frac {E}{\cos \delta } \\[ 5pt ] &=&\frac {\displaystyle \frac {6 \ 600}{\sqrt {3}}}{\cos 30°} \\[ 5pt ] &=&\frac {\displaystyle \frac {6 \ 600}{\sqrt {3}}}{\displaystyle \frac {\sqrt {3}}{2}} \\[ 5pt ] &=&4 \ 400 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，発電機の出力\( \ P \ \mathrm {[MW]} \ \)は，ワンポイント解説「2.同期発電機の出力」の通り，
\[
\begin{eqnarray}
P &=&\frac {3E_{0}E\sin \delta }{x_{\mathrm {s}}} \\[ 5pt ] &=&\frac {3\times 4 \ 400\times \displaystyle \frac {6 \ 600}{\sqrt {3}}\times \sin 30°}{4.763} \\[ 5pt ] &=&\frac {3\times 4 \ 400\times \displaystyle \frac {6 \ 600}{\sqrt {3}}\times \frac {1}{2}}{4.763} \\[ 5pt ] &≒&5 \ 280 \ 000 \ \mathrm {[W]}　→　5.28 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。