《機械》〈電気化学〉[H19:問13]電気めっき法により析出する亜鉛の量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

硫酸亜鉛\( \ \left( \mathrm {ZnSO_{4}}\right) \ \)／硫酸系の電解液の中で陽極に亜鉛を，陰極に鋼帯の原板を用いた電気めっき法はトタンの製造法として広く知られている。今，両電極間に\( \ 2 \ \mathrm {[A]} \ \)の電流を\( \ 5 \ \mathrm {[h]} \ \)通じたとき，原板に析出する亜鉛の量\( \ \mathrm {[g]} \ \)の値として，最も近いのは次のうちどれか。

ただし，亜鉛の原子価（反応電子数）は\( \ 2 \ \)，原子量は\( \ 65.4 \ \)，電流効率は\( \ 65 \ \mathrm {[％]} \ \)，ファラデ一定数\( \ F= 9.65\times 10^{4} \ \mathrm {[C/mol]} \ \)とする。

　(1)　\( \ 0.0022 \ \)　　(2)　\( \ 0.13 \ \)　　(3)　\( \ 0.31 \ \)　　(4)　\( \ 7.9 \ \)　　(5)　\( \ 16 \ \)

【ワンポイント解説】

電気めっき法により陰極に析出する亜鉛の量を計算する問題です。
電気めっきや電解精錬等様々な問題が出題されますが，ほとんどの金属の価数は\( \ 2 \ \)なので計算方法も似ています。
ファラデーの法則に関しては丸暗記して数値を代入することで解くことも可能ですが，できるだけ丸暗記に頼らず，解答のように理解して解く方法をお勧めします。

1.電気めっきの原理
電気めっき法は錆びやすい鉄の表面に異なる金属の薄膜を形成する方法で，鉄よりもイオン化傾向が大きい亜鉛をめっきしたものをトタン，イオン化傾向が小さいスズをめっきしたものをブリキといいます。
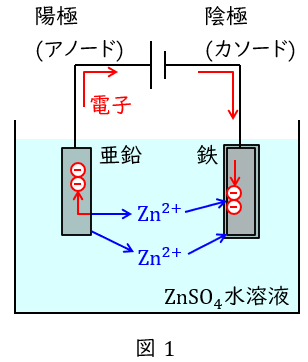
図1に示すように硫酸亜鉛水溶液中において陽極に亜鉛，陰極にめっきしたい金属（鉄等）を入れ通電すると，陽極と陰極では以下の反応が起こり，陰極に亜鉛が析出します。これにより薄膜が形成されます。

　陽極：\(\mathrm {Zn}　→　{\mathrm {Zn}}^{2+}　+　2\mathrm {e}^{-}\)
　陰極：\({\mathrm {Zn}}^{2+}　+　2\mathrm {e}^{-}　→　\mathrm {Zn}\)

2.電気分解におけるファラデーの法則
電極に析出する物質の質量\( \ W \ \mathrm {[g]} \ \)は溶液を通過する電気量\( \ Q \ \mathrm {[C]} \ \)に比例する（第\( \ 1 \ \)法則）もしくは物質の化学当量（＝原子量\( \ m \ \)／原子価\( \ n \ \)）に比例する（第\( \ 2 \ \)法則）という法則で，ファラデー定数を\( \ F≒96 \ 500 \ \mathrm {[C / mol]} \ \)とすると，
\[
\begin{eqnarray}
W&=&\frac {1}{F}\cdot \frac {m}{n} Q \\[ 5pt ] \end{eqnarray}
\] となります。また，電流\( \ I \ \mathrm {[A]} \ \)を時間\( \ t \ \mathrm {[s]} \ \)通電していたとすると，\( \ Q=It \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{F}\cdot \frac {m}{n} It \\[ 5pt ] \end{eqnarray}
\] となります。

※ファラデーの法則を覚えても良いですが，できるだけ単位や化学式を用いた解法をマスターするようにしましょう。

【解答】

解答：(4)
両電極間に\( \ I=2 \ \mathrm {[A]} \ \)を\( \ t=5 \ \mathrm {[h]} \ \)通電したときの電気量\( \ Q \ \mathrm {[C]} \ \)は，電流効率\( \ \eta =0.65 \ \)より，
\[
\begin{eqnarray}
Q&=&It\eta \\[ 5pt ] &=&2\times 5\times 3 \ 600 \times 0.65 \\[ 5pt ] &=&23 \ 400 \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] であり，電子のモル数\( \ N_{e} \ \mathrm {[mol]} \ \)は，ファラデー定数が\( \ F= 9.65\times 10^{4} \ \mathrm {[C/mol]} \ \)であることから，
\[
\begin{eqnarray}
N_{e}&=&\frac {Q}{F} \\[ 5pt ] &=&\frac {23 \ 400}{9.65\times 10^{4}} \\[ 5pt ] &≒&0.242 \ 5 \ \mathrm {[mol]} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，ワンポイント解説「1.電気めっきの原理」の通り，亜鉛の価数は\( \ 2 \ \)であるから，亜鉛のモル数\( \ N_{z} \ \mathrm {[mol]} \ \)は，
\[
\begin{eqnarray}
N_{z}&=&\frac {N_{e}}{2} \\[ 5pt ] &=&\frac {0.242 \ 5}{2} \\[ 5pt ] &≒&0.121 \ 3 \ \mathrm {[mol]} \\[ 5pt ] \end{eqnarray}
\] となるので，析出する亜鉛の量\( \ W \ \mathrm {[g]} \ \)は亜鉛の原子量\( \ M=65.4 \ \)より，
\[
\begin{eqnarray}
W&=&MN_{z} \\[ 5pt ] &=&65.4\times 0.121 \ 3 \\[ 5pt ] &≒&7.9 \ \mathrm {[g]} \\[ 5pt ] \end{eqnarray}
\] と求められる。