《機械》〈回転機〉[H24:問2]直流他励電動機の特性に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

直流他励電動機の電機子回路に直列抵抗\( \ 0.8 \ \mathrm {[\Omega ]} \ \)を接続して電圧\( \ 120 \ \mathrm {[V]} \ \)の直流電源で始動したところ，始動直後の電機子電流は\( \ 120 \ \mathrm {[A]} \ \)であった。電機子電流が\( \ 40 \ \mathrm {[A]} \ \)になったところで直列抵抗を\( \ 0.3 \ \mathrm {[\Omega ]} \ \)に切り換えた。インダクタンスが無視でき，電流が瞬時に変化するものとして，切換え直後の電機子電流\( \ \mathrm {[A]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，切換え時に電動機の回転速度は変化しないものとする。また，ブラシによる電圧降下及び電機子反作用はないものとし，電源電圧及び界磁電流は一定とする。

　(1)　\(60\)　　(2)　\(80\)　　(3)　\(107\)　　(4)　\(133\)　　(5)　\(240\)　

【ワンポイント解説】

解法を理解していれば難なく解ける問題ですが，初見の受験生だと少し手こずる問題かもしれません。まずは等価回路が描けることが大前提となりますので，確実に理解しておくようにしましょう。

1.他励直流電動機の等価回路
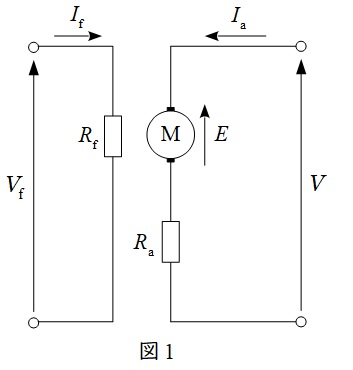
図1に他励直流電動機の等価回路を示します。図1において，\( \ V \ \)は端子電圧，\( \ E \ \)は逆起電力，\( \ V_{\mathrm {f}} \ \)は界磁電圧，\( \ I_{\mathrm {a}} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \)は界磁抵抗となります。
他励式の特徴としては，界磁回路が独立しているので，界磁磁束を独立して制御できるという特徴があります。

【解答】

解答：(2)
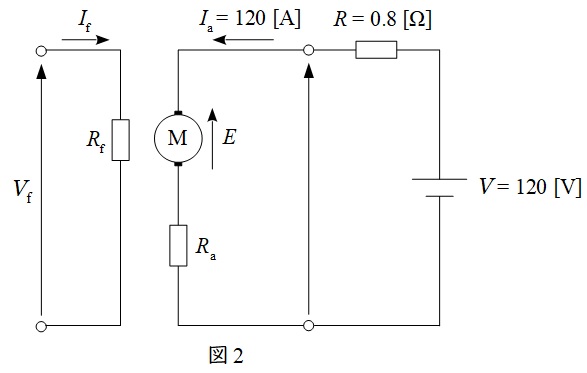
始動直後の等価回路を図2に示す。図2において，\( \ E=k\phi N \ \)の関係があるので，始動直後は\( \ N=0 \ \)であるから，\( \ E=0 \ \mathrm {[V]} \ \)となるので，電機子回路の回路方程式より，
\[
\begin{eqnarray}
V &=& RI_{\mathrm {a}}+E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] 120 &=& 0.8\times 120-0+R_{\mathrm {a}}\times 120 \\[ 5pt ] 120R_{\mathrm {a}} &=& 120-96 \\[ 5pt ] R_{\mathrm {a}} &=& 0.2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。　

次に，電動機の回転数が上がり，電機子電流が\( \ 40 \ \mathrm {[A]} \ \)になったときの等価回路を図3に示す。図3において，回路方程式より，
\[
\begin{eqnarray}
V &=& RI_{\mathrm {a}}+E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] 120 &=& 0.8\times 40+E+0.2\times 40 \\[ 5pt ] E &=& 120-32-8 \\[ 5pt ] &=& 80 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。

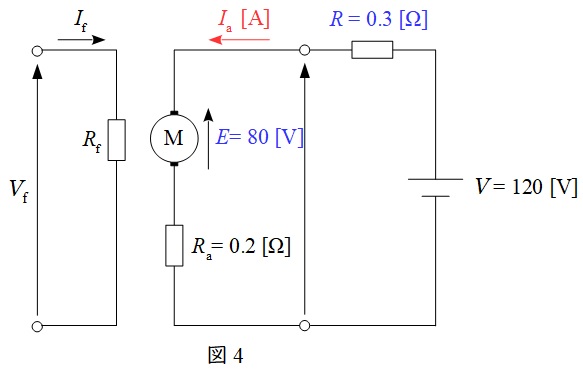
最後に，直列抵抗を\( \ 0.3 \ \mathrm {[\Omega ]} \ \)に切り換えたときの等価回路を図4に示す。図4において，回路方程式より，
\[
\begin{eqnarray}
V &=& RI_{\mathrm {a}}+E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] 120 &=& 0.3I_{\mathrm {a}}+80+0.2I_{\mathrm {a}} \\[ 5pt ] 0.5I_{\mathrm {a}} &=& 120-80 \\[ 5pt ] I_{\mathrm {a}} &=& 80 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。