《電力》〈配電〉[R07上:問17]負荷を追加した変圧器の過負荷運転防止に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格容量\( \ 750 \ \mathrm {kV\cdot A} \ \)の三相変圧器に遅れ力率\( \ 0.9 \ \)の三相負荷\( \ 500 \ \mathrm {kW} \ \)が接続されている。

この三相変圧器に新たに遅れ力率\( \ 0.8 \ \)の三相負荷\( \ 200 \ \mathrm {kW} \ \)を接続する場合，次の(a)及び(b)の問に答えよ。

(a)　負荷を追加した後の無効電力の値\( \ \mathrm {[kvar]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 472 \ \)　　(2)　\( \ 525 \ \)　　(3)　\( \ 339 \ \)　　(4)　\( \ 392 \ \)　　(5)　\( \ 610 \ \)

(b)　この変圧器の過負荷運転を回避するために，変圧器の二次側に必要な最小の電力用コンデンサ容量の値\( \ \mathrm {[kvar]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 70 \ \)　　(2)　\( \ 256 \ \)　　(3)　\( \ 203 \ \)　　(4)　\( \ 123 \ \)　　(5)　\( \ 50 \ \)

【ワンポイント解説】

変圧器に接続した負荷の無効電力と必要なコンデンサ容量を求める問題です。
用いられる公式はさほど難しいものではありませんが，少し計算量が多くなる問題と言えます。変圧器の定格容量は皮相電力，負荷の容量は有効電力であることに注意しましょう。
本問は平成24年問17からの再出題となります。

1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
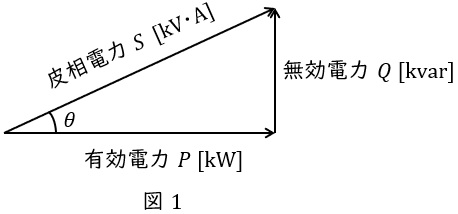
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(4)
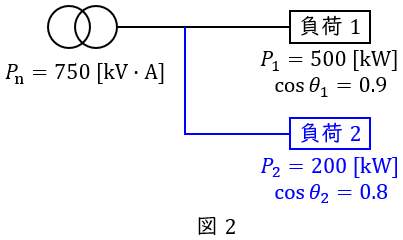
元々接続されていた力率\( \ 0.9 \ \)の負荷を負荷\( \ 1 \ \)，新たに接続した力率\( \ 0.8 \ \)の負荷を負荷\( \ 2 \ \)とし，それぞれの電力及び力率を図2の通りとする。
図2よりそれぞれの負荷の\( \ \sin \theta _{1} \ \)，\( \ \sin \theta _{2} \ \)は，\( \ \sin ^{2}\theta +\cos ^{2}\theta =1 \ \)であるから，
\[
\begin{eqnarray}
\sin \theta _{1} &=&\sqrt {1-\cos ^{2}\theta _{1} } \\[ 5pt ] &=&\sqrt {1-0.9 ^{2} } \\[ 5pt ] &≒&0.435 \ 9 \\[ 5pt ] \sin \theta _{2} &=&\sqrt {1-\cos ^{2}\theta _{2} } \\[ 5pt ] &=&\sqrt {1-0.8 ^{2} } \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] となり，それぞれの無効電力の大きさ\( \ Q _{1} \ \mathrm {[kvar]} \ \)，\( \ Q _{2} \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q _{1}&=&\frac {P_{1}}{\cos \theta _{1}}\cdot \sin \theta _{1} \\[ 5pt ] &=&\frac {500}{0.9}\times 0.435 \ 9 \\[ 5pt ] &≒&242.2 \ \mathrm {[kvar]} \\[ 5pt ] Q _{2}&=&\frac {P_{2}}{\cos \theta _{2}}\cdot \sin \theta _{2} \\[ 5pt ] &=&\frac {200}{0.8}\times 0.6 \\[ 5pt ] &=&150 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
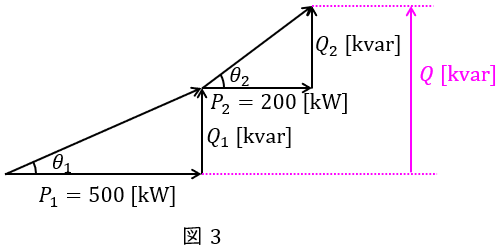
\] となる。したがって，負荷\( \ 1 \ \)と負荷\( \ 2 \ \)を合成したベクトル図は図3のようになるので，全体の無効電力\( \ Q \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q&=&Q _{1}+Q _{2} \\[ 5pt ] &=&242.2+150 \\[ 5pt ] &=&392.2　→　392 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
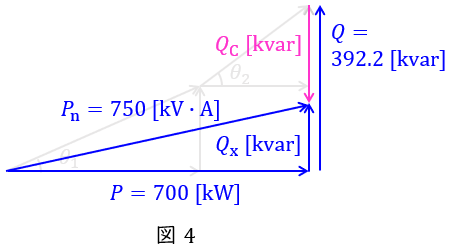
負荷\( \ 2 \ \)を接続し，さらにコンデンサ接続した後の全体のベクトル図は図4のようになる。
図4より，変圧器が過負荷とならない最大無効電力\( \ Q_{\mathrm {x}} \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {x}}&=&\sqrt {S^{2}-P^{2}} \\[ 5pt ] &=&\sqrt {750^{2}-700^{2}} \\[ 5pt ] &≒&269.3 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] であるから，過負荷とならないための最小の電力用コンデンサ容量\( \ Q_{\mathrm {C}} \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&Q-Q_{\mathrm {x}} \\[ 5pt ] &=&392.2-269.3 \\[ 5pt ] &=&122.9　→　123 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。