Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,直流電動機に関する記述である。
直流分巻電動機は界磁回路と電機子回路とが並列に接続されており,端子電圧及び界磁抵抗を一定にすれば,界磁磁束は一定である。このとき,機械的な負荷が\(\fbox { (ア) }\)すると,電機子電流が\(\fbox { (イ) }\)し回転速度はわずかに\(\fbox { (ウ) }\)するが,ほぼ一定である。このように負荷の変化に関係なく,回転速度がほぼ一定な電動機は定速度電動機と呼ばれる。
上記のように直流分巻電動機の界磁磁束を一定にして運転した場合,電機子反作用等を無視すると,トルクは電機子電流にほぼ\(\fbox { (エ) }\)する。
一方,直流直巻電動機は界磁回路と電機子回路とが直列に接続されており,界磁磁束は負荷電流によって作られる。界磁磁束が磁気飽和しない領域では,界磁磁束は負荷電流にほぼ\(\fbox { (エ) }\)し,トルクは負荷電流の\(\fbox { (オ) }\)にほぼ比例する。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\
\hline
(1) & 減 少 & 減 少 & 増 加 & 反比例 & \displaystyle \frac {1}{2}乗 \\
\hline
(2) & 増 加 & 増 加 & 増 加 & 比 例 & 2乗 \\
\hline
(3) & 減 少 & 増 加 & 減 少 & 反比例 & \displaystyle \frac {1}{2}乗 \\
\hline
(4) & 増 加 & 増 加 & 減 少 & 比 例 & 2乗 \\
\hline
(5) & 減 少 & 減 少 & 減 少 & 比 例 & \displaystyle \frac {1}{2}乗 \\
\hline
\end{array}
\]
【ワンポイント解説】
回転機の問題は等価回路を描いて,等価回路から考えて答えを導き出すことが肝要となります。等価回路は確実に描けるようにしておきましょう。
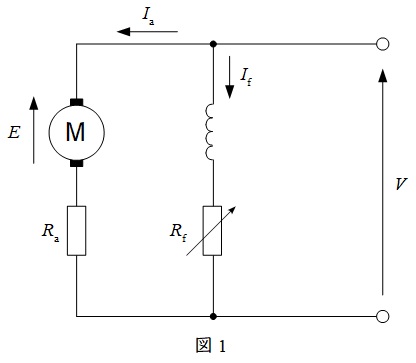
1.分巻電動機の等価回路
分巻電動機の等価回路を図1に示します。ここで\(V\)は端子電圧,\(E\)は逆起電力,\(I_{\mathrm {f}}\)は界磁電流,\(I_{\mathrm {a}}\)は電機子電流,\(R_{\mathrm {f}}\)は界磁抵抗,\(R_{\mathrm {a}}\)は電機子抵抗となります。
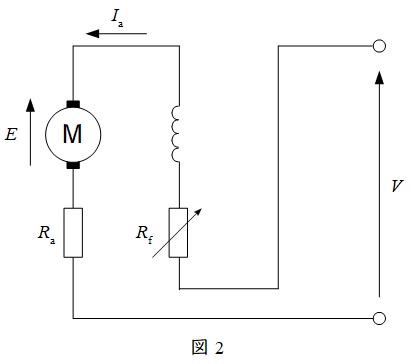
2.直巻電動機の等価回路
直巻電動機の等価回路を図2に示します。ここで\(V\)は端子電圧,\(E\)は逆起電力,\(I_{\mathrm {a}}\)は電機子電流,\(R_{\mathrm {f}}\)は界磁抵抗,\(R_{\mathrm {a}}\)は電機子抵抗となります。電機子回路と界磁回路が直列なので,電機子電流と界磁電流が等しくなります。
【解答】
解答:(4)
(ア)
(イ)
(ウ)
図1において,電動機の出力\(P\)は\(P=EI_{\mathrm {a}}\)で与えられ,負荷が増加すると,電機子電流が増加し,負荷が減少すると,電機子電流が減少する。また,逆起電力\(E\)は
\[
E=V-R_{\mathrm {a}}I_{\mathrm {a}}
\]
となり,わずかではあるが,負荷が増加すると逆起電力は減少する。逆起電力と回転速度は比例の関係であるので,負荷が増加すると回転速度はわずかに減少する。
よって,正しい組合せは(ア)増加,(イ)増加,(ウ)減少もしくは(ア)減少,(イ)減少,(ウ)増加のどちらかとなる。
(エ)
直流分巻電動機においてトルクは出力に比例し,出力は電機子電流に比例するため,比例となる。
直流直巻電動機において,界磁電流と電機子電流は等しいので,界磁磁束と電機子電流は比例する。
(オ)
直流直巻電動機においては,逆起電力が界磁磁束に比例し,界磁磁束が電機子電流に比例する。またトルクは出力に比例し, \(P=EI_{\mathrm {a}}\)となるので,トルクは電機子電流の2乗に比例する。





















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは