《機械》〈回転機〉[H24:問4]三相誘導電動機の効率に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

三相誘導電動機があり，一次巻線抵抗が\( \ 15 \ \mathrm {[\Omega ]} \ \)，一次側に換算した二次巻線抵抗が\( \ 9 \ \mathrm {[\Omega ]} \ \)，滑りが\( \ 0.1 \ \)のとき，効率\( \ \mathrm {[％]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，励磁電流は無視できるものとし，損失は，一次巻線による銅損と二次巻線による銅損しか存在しないものとする。

(1)　\(75\)　　(2)　\(77\)　　(3)　\(79\)　　(4)　\(82\)　　(5)　\(85\)

【ワンポイント解説】

等価回路をきちんと描くことができれば，問題なく解ける問題となります。効率の考え方は変圧器等にも応用できる内容です。確実に理解しておいて下さい。

1.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
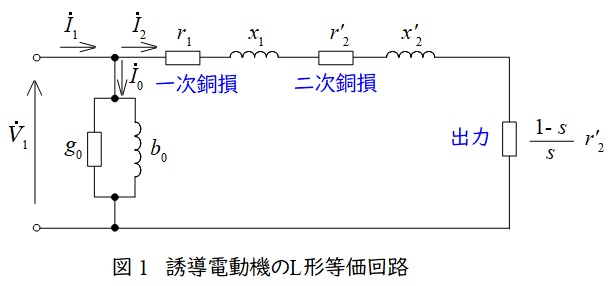
誘導電動機のL形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
図1より，出力\( \ P_{\mathrm {o}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& 3r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力\( \ P_{2} \ \)，出力\( \ P_{\mathrm {o}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

2.三相誘導電動機の効率\( \ \eta \ \)
三相誘導電動機の一次入力が\( \ P_{\mathrm {1}} \ \)，二次入力が\( \ P_{\mathrm {2}} \ \)，出力が\( \ P_{\mathrm {o}} \ \)，鉄損が\( \ P_{\mathrm {i}} \ \)，一次銅損が\( \ P_{\mathrm {c1}} \ \)，二次銅損が\( \ P_{\mathrm {c2}} \ \)であった時，各入力，出力の関係は，
\[
\begin{eqnarray}
P_{\mathrm {2}} &=&P_{\mathrm {1}}-P_{\mathrm {i}}-P_{\mathrm {c1}} \\[ 5pt ] P_{\mathrm {o}} &=&P_{\mathrm {2}}-P_{\mathrm {c2}} \\[ 5pt ] &=&P_{\mathrm {1}}-P_{\mathrm {i}}-P_{\mathrm {c1}}-P_{\mathrm {c2}} \\[ 5pt ] \end{eqnarray}
\] となるので，誘導電動機の効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {1}}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {o}}+P_{\mathrm {i}}+P_{\mathrm {c1}}+P_{\mathrm {c2}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
図1の\( \ \mathrm {L} \ \)形等価回路において，励磁回路には電流が流れないので，\( \ I_{0} =0 \ \)，\( \ I_{1}=I_{2}=I \ \)とすると，出力\( \ P_{\mathrm {o}} \ \)，一次銅損\( \ P_{\mathrm {c1}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)の大きさは，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=&3\frac {1-s}{s}{r_{2}}^{\prime }I^{2} \\[ 5pt ] &=&3\times \frac {1-0.1}{0.1}\times 9I^{2} \\[ 5pt ] &=&243I^{2} \\[ 5pt ] P_{\mathrm {c1}} &=&3r_{1}I^{2} \\[ 5pt ] &=&45I^{2} \\[ 5pt ] P_{\mathrm {c2}} &=&3{r_{2}}^{\prime }I^{2} \\[ 5pt ] &=&27I^{2} \\[ 5pt ] \end{eqnarray}
\] となるので，三相誘導電動機の効率\( \ \eta \ \mathrm {[％]} \ \)は，ワンポイント解説「2.三相誘導電動機の効率\( \ \eta \ \)」より，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {o}}+P_{\mathrm {c1}}+P_{\mathrm {c2}}}\times 100 \\[ 5pt ] &=&\frac {243I^{2}}{243I^{2}+45I^{2}+27I^{2}}\times 100 \\[ 5pt ] &=&\frac {243}{243+45+27}\times 100 \\[ 5pt ] &≒&77 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。