Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
ある事業所内における\( \ \mathrm {A} \ \)工場及び\( \ \mathrm {B} \ \)工場の,それぞれのある日の負荷曲線は図のようであった。それぞれの工場の設備容量が,\( \ \mathrm {A} \ \)工場では\( \ 400 \ \mathrm {kW} \ \),\( \ \mathrm {B} \ \)工場では\( \ 700 \ \mathrm {kW} \ \)であるとき,次の(a)及び(b)の問に答えよ。
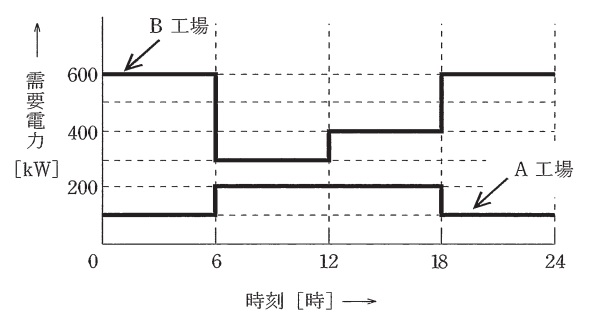
(a) \( \ \mathrm {A} \ \)工場及び\( \ \mathrm {B} \ \)工場を合わせた需要率の値\( \ [%] \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 54.5 \ \) (2) \( \ 56.8 \ \) (3) \( \ 63.6 \ \) (4) \( \ 89.3 \ \) (5) \( \ 90.4 \ \)
(b) \( \ \mathrm {A} \ \)工場及び\( \ \mathrm {B} \ \)工場を合わせた総合負荷率の値\( \ [%] \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 56.8 \ \) (2) \( \ 63.6 \ \) (3) \( \ 78.1 \ \) (4) \( \ 89.3 \ \) (5) \( \ 91.6 \ \)
【ワンポイント解説】
需要率,負荷率に関する問題で,法規では非常に頻出となる問題で,本問が解けるかどうかが合否に大きく影響すると言っても過言ではないと思います。需要率,不等率,負荷率の定義は試験本番までに確実に暗記しておくようにしておきましょう。
1.需要率,不等率,負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100 [%] \\[ 5pt ]
\end{eqnarray}
\]
②不等率(常に\( \ 1 \ \)以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ]
\end{eqnarray}
\]
③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100 [%] \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(a)解答:(3)
\( \ \mathrm {A} \ \)工場及び\( \ \mathrm {B} \ \)工場を合成した需要電力は,
\[
\begin{eqnarray}
0 \ 時 \ &~& \ 6 \ 時&:&700 \ \mathrm {kW} \\[ 5pt ]
6 \ 時 \ &~& \ 12 \ 時&:&500 \ \mathrm {kW} \\[ 5pt ]
12 \ 時 \ &~& \ 18 \ 時&:&600 \ \mathrm {kW} \\[ 5pt ]
18 \ 時 \ &~& \ 24 \ 時&:&700 \ \mathrm {kW} \\[ 5pt ]
\end{eqnarray}
\]
であるから,その最大需要電力は,\( \ 700 \ \mathrm {kW} \ \)となる。
よって需要率は,ワンポイント解説「1.需要率,不等率,負荷率の定義」の通り,
\[
\begin{eqnarray}
需要率 &=&\frac {最大需要電力}{設備容量}\times 100 \\[ 5pt ]
&=&\frac {700}{400+700}\times 100 \\[ 5pt ]
&≒&63.6 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
\( \ \mathrm {A} \ \)工場及び\( \ \mathrm {B} \ \)工場を合成した平均電力は,
\[
\begin{eqnarray}
平均電力 &=&\frac {700+500+600+700}{4} \\[ 5pt ]
&=&625 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,負荷率は,ワンポイント解説「1.需要率,不等率,負荷率の定義」より,
\[
\begin{eqnarray}
負荷率 &=&\frac {平均需要電力}{最大需要電力}\times 100 \\[ 5pt ]
&=&\frac {625}{700}\times 100 \\[ 5pt ]
&≒&89.3 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは