Contents
【問題】
【難易度】★★★★☆(やや難しい)
三相3線式,受電電圧\( \ 6.6 \ \mathrm {kV} \ \),周波数\( \ 50 \ \mathrm {Hz} \ \)の自家用電気設備を有する需要家が,直列リアクトルと進相コンデンサからなる定格設備容量\( \ 100 \ \mathrm {kvar} \ \)の進相設備を施設することを計画した。この計画におけるリアクトルには,当該需要家の遊休中の進相設備から直列リアクトルのみを流用することとした。施設する進相設備の進相コンデンサのインピーダンスを基準として,これを\( \ \mathrm {-j100} \ % \ \)と考えて,次の(a)及び(b)の問に答えよ。
なお,関係する機器の仕様は,次のとおりである。
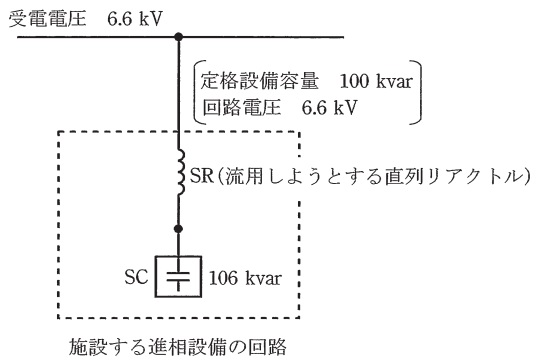
・施設する進相コンデンサ:回路電圧\( \ 6.6 \ \mathrm {kV} \ \),周波数\( \ 50 \ \mathrm {Hz} \ \),
定格容量三相\( \ 106 \ \mathrm {kvar} \ \)
・遊休中の進相設備:回路電圧\( \ 6.6 \ \mathrm {kV} \ \),周波数\( \ 50 \ \mathrm {Hz} \ \),
進相コンデンサ 定格容量三相\( \ 160 \ \mathrm {kvar} \ \)
直列リアクトル 進相コンデンサのインピーダンスの\( \ 6 \ % \ \)
(a) 回路電圧\( \ 6.6 \ \mathrm {kV} \ \)のとき,施設する進相設備のコンデンサの端子電圧の値\([V]\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 6600 \ \) (2) \( \ 6875 \ \) (3) \( \ 7020 \ \) (4) \( \ 7170 \ \) (5) \( \ 7590 \ \)
(b) この計画における進相設備の,第5調波の影響に関する対応について,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) インピーダンスが\( \ 0 \ % \ \)の共振状態に近くなり,過電流により流用しようとするリアクトルとコンデンサは共に焼損のおそれがあるため,本計画の機器流用は危険であり,流用してはならない。
(2) インピーダンスが約\( \ \mathrm {-j10} \ % \ \)となり進み電流が多く流れ,流用しようとするリアクトルの高調波耐量が保証されている確認をしたうえで流用する必要がある。
(3) インピーダンスが約\( \ \mathrm {+j10} \ % \ \)となり遅れ電流が多く流れ,流用しようとするリアクトルの高調波耐量が保証されている確認をしたうえで流用する必要がある。
(4) インピーダンスが約\( \ \mathrm {-j25} \ % \ \)となり進み電流が流れ,流用しようとするリアクトルの高調波耐量を確認したうえで流用する必要がある。
(5) インピーダンスが約\( \ \mathrm {+j25} \ % \ \)となり遅れ電流が流れ,流用しようとするリアクトルの高調波耐量を確認したうえで流用する必要がある。
【ワンポイント解説】
問題文を確実に理解する能力と百分率インピーダンスの計算を確実に行えるスキルが求められる問題で,三種としてはかなり難しい問題と言えます。(a),(b)共にかなり正答率は低いと思われますが,この問題は配点も高いので,よく理解しておくようにして下さい。
1.百分率インピーダンスの容量変換
基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ基準容量を変化する場合のパーセントインピーダンスは,
\[
%Z_{\mathrm {B}}=\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}\times %Z_{\mathrm {A}}
\]
となります。
2.高調波におけるリアクトルとコンデンサのリアクタンス計算方法
リアクトルのリアクタンス\( \ X_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {L}} &=&\omega L \\[ 5pt ]
&=&2\pi f L \\[ 5pt ]
\end{eqnarray}
\]
となり,周波数\( \ f \ \)に比例するので,第\( \ n \ \)次高調波でのリアクタンスは\( \ n \ \)倍となります。
一方,コンデンサのリアクタンス\( \ X_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {C}} &=&\frac {1}{\omega C} \\[ 5pt ]
&=&\frac {1}{2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
となり,周波数\( \ f \ \)に反比例するので,第\( \ n \ \)次高調波でのリアクタンスは\( \ \displaystyle \frac {1}{n} \ \)倍となります。
【解答】
(a)解答:(2)
ワンポイント解説「1.百分率インピーダンスの容量変換」より,\( \ 106 \ \mathrm {kvar} \ \)ベースの直列リアクトルの百分率インピーダンスの大きさ\( \ %X_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
%X_{\mathrm {L}} &=& \frac {106}{160}\times 6 \\[ 5pt ]
&=&3.975 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,コンデンサの端子電圧の値\( \ V_{\mathrm {C}} \ \)は分圧の法則より,
\[
\begin{eqnarray}
\frac {V_{\mathrm {C}}}{\sqrt {3}} &=&\frac {-100}{-100+3.975}\times \frac {6600}{\sqrt {3}} \\[ 5pt ]
V_{\mathrm {C}} &=& \sqrt {3} \left( \frac {-100}{-100+3.975}\times \frac {6600}{\sqrt {3}}\right) \\[ 5pt ]
&≒&6873 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,最も近い値は\( \ 6875 \ \mathrm {V} \ \)となる。
※ 本問は\( \ 3.975 \ \)を\( \ 4.00 \ \)と概算すれば\( \ 6875 \ \mathrm {V} \ \)と求められます。
(b)解答:(1)
ワンポイント解説「1.2.高調波におけるリアクトルとコンデンサのリアクタンス計算方法」より,第5調波におけるリアクトルとコンデンサの百分率リアクタンスは,
\[
\begin{eqnarray}
%X_{\mathrm {L5}} &=&3.975\times 5\\[ 5pt ]
&=&19.875 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
%X_{\mathrm {C5}} &=&\frac {100}{5} \\[ 5pt ]
&=&20 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その合成インピーダンスはほぼ零となる。したがって,共振状態に近くなり,リアクトルとコンデンサは共に焼損するおそれがある。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは