Contents
【問題】
【難易度】★★★★☆(やや難しい)
伝熱に関する次の(a)及び(b)の問に答えよ。
(a) 直径\( \ 1 \ \mathrm {[m]} \ \),高さ\( \ 0.5 \ \mathrm {[m]} \ \)の円柱がある。円柱の下面温度が\( \ 600 \ \mathrm {[K]} \ \),上面温度が\( \ 330 \ \mathrm {[K]} \ \)に保たれているとき,伝導によって円柱の高さ方向に流れる熱流\( \ \mathrm {[W]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,円柱の熱伝導率は\( \ 0.26 \ \mathrm {[W / \left( m\cdot K\right) ]} \ \)とする。また,円柱側面からの放射及び対流による熱損失はないものとする。
(1) \(45\) (2) \(110\) (3) \(441\) (4) \(661\) (5) \(1630\)
(b) 次の文章は,放射伝熱に関する記述である。
すべての物体はその物体の温度に応じた強さのエネルギーを\( \ \fbox { (ア) } \ \)として放出している。その量は物体表面の温度と放射率とから求めることができる。
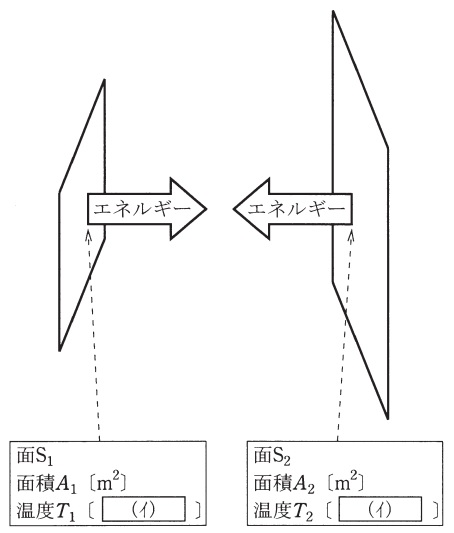
いま,図に示すように,面積\( \ A_{1} \ \mathrm {[m^{2}]} \ \),温度\( \ T_{1} \ \mathrm {[ \ \fbox { (イ) } \ ]} \ \)の面\( \ \mathrm {S}_{1} \ \)と,面積\( \ A_{2} \ \mathrm {[m^{2}]} \ \),温度\( \ T_{2} \ \mathrm {[ \ \fbox { (イ) } \ ]} \ \)の面\( \ \mathrm {S}_{2} \ \)とが向き合っている。両面の温度に\( \ T_{1} \ > \ T_{2} \ \)の関係があるとき,エネルギーは面\( \ \mathrm {S}_{1} \ \)から面\( \ \mathrm {S}_{2} \ \)に放射によって伝わる。このエネルギー流量(\( \ 1 \ \)秒当たりに面\( \ \mathrm {S}_{1} \ \)から面\( \ \mathrm {S}_{2} \ \)に伝わるエネルギー)\( \ \mathit {\Phi } \ \mathrm {[W]} \ \)は\( \ \mathit {\Phi }=\varepsilon \sigma A_{1}F_{12}\times \fbox { (ウ) } \ \)で与えられる。
ここで,\( \ \varepsilon \ \)は放射率,\( \ \sigma \ \)は\( \ \fbox { (エ) } \ \),及び\( \ F_{12} \ \)は形態係数である。ただし,\( \ \varepsilon \ \)に波長依存性はなく,両面において等しいとする。また,\( \ F_{12} \ \)は面\( \ \mathrm {S}_{1} \ \),面\( \ \mathrm {S}_{2} \ \)の大きさ,形状,相対位置などの幾何学的な関係で決まる値である。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 電磁波 & \mathrm {K} & \left( T_{1}-T_{2}\right) & プランク定数 \\
\hline
(2) & 熱 & \mathrm {K} & \left( {T_{1}}^{4}-{T_{2}}^{4}\right) & ステファン・ボルツマン定数 \\
\hline
(3) & 電磁波 & \mathrm {K} & \left( {T_{1}}^{4}-{T_{2}}^{4}\right) & ステファン・ボルツマン定数 \\
\hline
(4) & 熱 & \mathrm {℃} & \left( T_{1}-T_{2}\right) & ステファン・ボルツマン定数 \\
\hline
(5) & 電磁波 & \mathrm {℃} & \left( {T_{1}}^{4}-{T_{2}}^{4}\right) & プランク定数 \\
\hline
\end{array}
\]
【ワンポイント解説】
熱伝導がなぜ電験?という質問をたまに受けますが,本問のような熱伝導の内容は電気回路のオームの法則と似ているため出題されると考えられます。電気回路のように複雑な問題は出題されないので,本問が解けるようになっていれば,対策としては十分と言えると思います。
1.熱力学におけるオームの法則
物体の温度差を\( \ \theta \ \mathrm {[K]} \ \),熱抵抗を\( \ R \ \mathrm {[K / W]} \ \)とすると,物体の熱流\( \ I \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
I &=& \frac {\theta }{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)
物体の熱伝導率が\( \ \lambda \ \mathrm {[W / (m\cdot K )]} \ \),断面積が\( \ S \ \mathrm {[m^{2}]} \ \),長さが\( \ l \ \mathrm {[m]} \ \)であるとき,物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)は,
\[
\begin{eqnarray}
R &=& \frac {l}{\lambda S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(2)
題意より,円柱物体の断面積\( \ S \ \mathrm {[m^{2}]} \ \)は,
\[
\begin{eqnarray}
S &=& \pi \times \left( \frac {1}{2} \right) ^{2} \\[ 5pt ]
&≒& 0.7854 \ \mathrm {[m^{2}]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)は,ワンポイント解説「2.物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)」より,
\[
\begin{eqnarray}
R &=& \frac {l}{\lambda S} \\[ 5pt ]
&=& \frac {0.5}{0.26 \times 0.7854} \\[ 5pt ]
&≒& 2.449 \ \mathrm {[K / W]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ワンポイント解説「1.熱力学におけるオームの法則」より,伝導によって円柱の高さ方向に流れる熱流\( \ I \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
I &=& \frac {600-330}{2.449} \\[ 5pt ]
&≒& 110 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
(ア)
放射伝熱の場合は,物体の温度に応じた強さの電磁波を放出していると考えます。したがって,熱だと伝わらない空間中に何もない状態(真空)でもエネルギーを放出します。
(イ)
熱力学においては,基本的に絶対零度を基準とした単位である\( \ \mathrm {[K]} \ \)を用います。
(ウ)
放射のエネルギーは絶対温度の4乗に比例します。
(エ)
放射伝熱の式に係る\( \ \sigma \ \)はステファン・ボルツマン定数と言います。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは