【問題】
【難易度】★★★☆☆(普通)
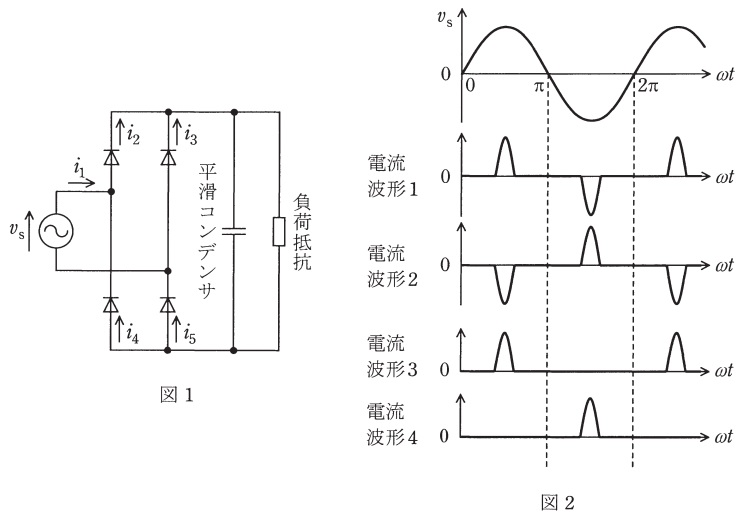
図1は,平滑コンデンサをもつ単相ダイオードブリッジ整流器の基本回路である。なお,この回路のままでは電流波形に高調波が多く含まれるので,実用化に当たっては注意が必要である。
図1の基本回路において,一定の角周波数\( \ \omega \ \)の交流電源電圧を\( \ v_{\mathrm {s}} \ \),電源電流を\( \ i_{1} \ \),図中のダイオードの電流を\( \ i_{2} \ \),\( \ i_{3} \ \),\( \ i_{4} \ \),\( \ i_{5} \ \)とする。平滑コンデンサの静電容量は,負荷抵抗の値とで決まる時定数が電源の\( \ 1 \ \)周期に対して十分に大きくなるように選ばれている。図2は交流電源電圧\( \ v_{\mathrm {s}} \ \)に対する各部の電流波形の候補を示している。図1の電流\( \ i_{1} \ \),\( \ i_{2} \ \),\( \ i_{3} \ \),\( \ i_{4} \ \),\( \ i_{5} \ \)の波形として正しい組合せを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& i_{1} & i_{2} & i_{3} & i_{4} & i_{5} \\
\hline
(1) & 電流波形1 & 電流波形4 & 電流波形3 & 電流波形3 & 電流波形4 \\
\hline
(2) & 電流波形2 & 電流波形3 & 電流波形4 & 電流波形4 & 電流波形3 \\
\hline
(3) & 電流波形1 & 電流波形4 & 電流波形3 & 電流波形4 & 電流波形3 \\
\hline
(4) & 電流波形2 & 電流波形4 & 電流波形3 & 電流波形3 & 電流波形4 \\
\hline
(5) & 電流波形1 & 電流波形3 & 電流波形4 & 電流波形4 & 電流波形3 \\
\hline
\end{array}
\]
【ワンポイント解説】
本問のようなブリッジ回路は毎年のように出題され,一種や二種試験でも出題される機械科目の中でも最重要項目です。過去問を何度も繰り返し,整流回路のメカニズムを理解するようにしましょう。
1.単相ダイオードブリッジ整流回路の動作
図3,図4に示す単相ダイオードブリッジ整流回路は以下のように動作します。
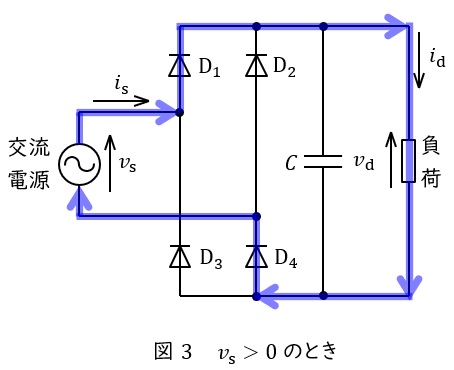
①\( \ v_{\mathrm {s}}>0 \ \)のとき
図3のように,電流は交流電源→\( \ \mathrm {D}_{1} \ \)→負荷→\( \ \mathrm {D}_{4} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると,入力電圧\( \ v_{\mathrm {s}} \ \)と等しくなります。
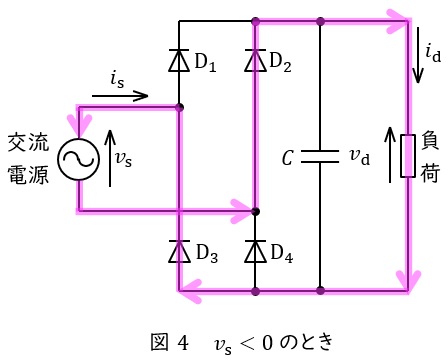
②\( \ v_{\mathrm {s}}<0 \ \)のとき
図4のように,電流は交流電源→\( \ \mathrm {D}_{2} \ \)→負荷→\( \ \mathrm {D}_{3} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {d}} \ \)は素子の電圧降下が無視できるとすると,\( \ -v_{\mathrm {s}} \ \)となります。
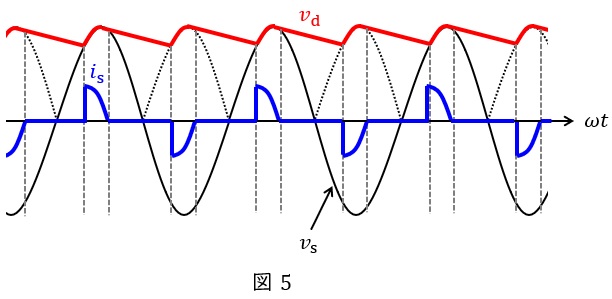
全体の波形は図5のようになり,平滑コンデンサ\( \ C \ \)により,出力電圧\( \ v_{\mathrm {d}} \ \)がほぼ一定になるように維持されます。
その間は,コンデンサから出力側に電荷が供給されることになることになるので,各ダイオードには電流は流れず,グラフに示すように入力電流\( \ i_{\mathrm {s}} \ \)も流れないことになります。
【関連する「電気の神髄」記事】
【解答】
解答:(5)
ワンポイント解説「1.単相ダイオードブリッジ整流回路の動作」の通り,\( \ v_{\mathrm {s}} \ \)が正の時は\( \ \mathrm {D}_{2} \ \),\( \ \mathrm {D}_{5} \ \)が導通して負荷抵抗に電流が流れ,\( \ i_{1} \ \)が正,\( \ i_{2} \ \)が正,\( \ i_{5} \ \)が正,の電流が流れます。\( \ i_{3} \ \),\( \ i_{4} \ \)は\( \ 0 \ \)のままとなります。
一方,\( \ v_{\mathrm {s}} \ \)が負の時は\( \ \mathrm {D}_{3} \ \),\( \ \mathrm {D}_{4} \ \)が導通して負荷抵抗に電流の流れ,\( \ i_{1} \ \)が負,\( \ i_{3} \ \)が正,\( \ i_{4} \ \)が正,の電流が流れます。\( \ i_{2} \ \),\( \ i_{5} \ \)は\( \ 0 \ \)のままとなります。
以上から,正しい組み合わせは(5)となります。




















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは