Contents
【問題】
【難易度】★★★★☆(やや難しい)
公称電圧\( \ 6600 \ \mathrm {[V]} \ \),周波数\( \ 50 \ \mathrm {[Hz]} \ \)の三相\( \ 3 \ \)線式配電線路から受電する需要家の竣工時における自主検査で,高圧引込ケーブルの交流絶縁耐力試験を「電気設備技術基準の解釈」に基づき実施する場合,次の(a)及び(b)の問に答えよ。
ただし,試験回路は図のとおりとし,この試験は\( \ 3 \ \)線一括で実施し,高圧引込ケーブル以外の電気工作物は接続されないものとし,各試験器の損失は無視する。
また,試験対象物である高圧引込ケーブル及び交流絶縁耐力試験に使用する試験器等の仕様は,次のとおりである。
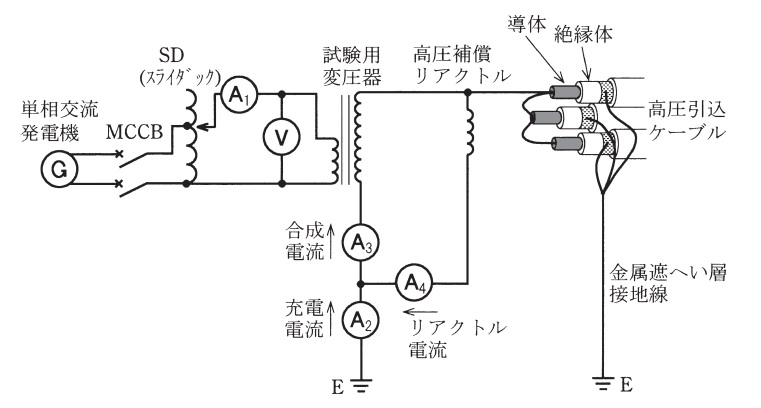
〇高圧引込ケーブルの仕様
\[
\begin{array}{|c|c|c|c|}
\hline
ケーブルの種類 & 公称断面積 & ケーブルのこう長 & 1 \ 線の対地静電容量 \\
\hline
6600 \ \mathrm {V} \ \mathrm {CVT} & 38 \ \mathrm {[{mm}^{2}]} & 150 \ \mathrm {[m]} & 0.22 \ \mathrm {[\mu F /km]} \\
\hline
\end{array}
\]
〇試験で使用する機器の仕様
\[
\begin{array}{|c|c|c|c|}
\hline
\displaystyle {試験機器}\atop \displaystyle {の名称} & 定 格 & \displaystyle {台数}\atop \displaystyle {[台]} & 備 考 \\
\hline
\displaystyle {試 験 用}\atop \displaystyle {変 圧 器} & \begin{matrix}
入力電圧 : 0-130 \ \mathrm {[V]} \\
出力電圧 : 0-13 \ \mathrm {[kV]} \\
巻数比 : 1/100 \\
30 \ 分連続許容出力電流 : 400 \ \mathrm {[mA]},50 \ \mathrm {[Hz]} \\
\end{matrix} & 1 & 電流計付 \\
\hline
\displaystyle {高圧補償}\atop \displaystyle {リアクトル} & \begin{matrix}
許容印加電圧 : 13 \ \mathrm {[kV]} \\
印加電圧 : 13 \ \mathrm {[kV]},50 \ \mathrm {[Hz]}使用時での電流 \ 300 \ \mathrm {[mA]} \\
\end{matrix} & 1 & 電流計付 \\
\hline
\displaystyle {単相交流}\atop \displaystyle {発電機} & 携帯用交流発電機 \ 出力電圧 \ 100 \ \mathrm {[V]},50 \ \mathrm {[Hz]} & 1 & インバータ方式 \\
\hline
\end{array}
\]
(a) 交流絶縁耐力試験における試験電圧印加時,高圧引込ケーブルの\( \ 3 \ \)線一括の充電電流(電流計\( \ \mathrm {A_{2}} \ \)の読み)に最も近い電流値\( \ \mathrm {[mA]} \ \)を次の(1)~(5)のうちから一つ選べ。
(1) \( \ 80 \ \) (2) \( \ 110 \ \) (3) \( \ 250 \ \) (4) \( \ 330 \ \) (5) \( \ 410 \ \)
(b) この絶縁耐力試験で必要な電源容量として,単相交流発電機に求められる最小の容量\( \ \mathrm {[kV\cdot A]} \ \)に最も近い数値を次の(1)~(5)のうちから一つ選べ。
(1) \( \ 1.0 \ \) (2) \( \ 1.5 \ \) (3) \( \ 2.0 \ \) (4) \( \ 2.5 \ \) (5) \( \ 3.0 \ \)
【ワンポイント解説】
試験電圧の知識,表の読み取り,充電電流の計算と知識と計算能力が求められる総合的な問題で,レベルとしてはかなり高い難問と言えると思います。こういう問題は類題が出題されやすい傾向にあります。よく理解しておくようにしましょう。
1.最大使用電圧
最大使用電圧は下表のとおりとなりますが,電験で出題されるのは係数\(\displaystyle \frac {1.15}{1.1}\)のみです。
<電気設備の技術基準の解釈第1条(抜粋)>
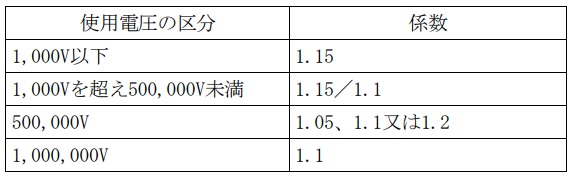
2.試験電圧
試験電圧は下表の通り細かく分かれています。最初に覚えておくべき内容は交流の試験電圧で,
\( \ 1.5 \ \times \ \)最大使用電圧 (最大使用電圧が\( \ 7 \ 000 \ \mathrm {V} \ \)以下の時)
\( \ 1.25 \ \times \ \)最大使用電圧 (最大使用電圧が\( \ 7 \ 000 \ \mathrm {V} \ \)を超え\( \ 60 \ 000 \ \mathrm {V} \ \)以下の時)
となります。
<電気設備の技術基準の解釈第15条(抜粋)>
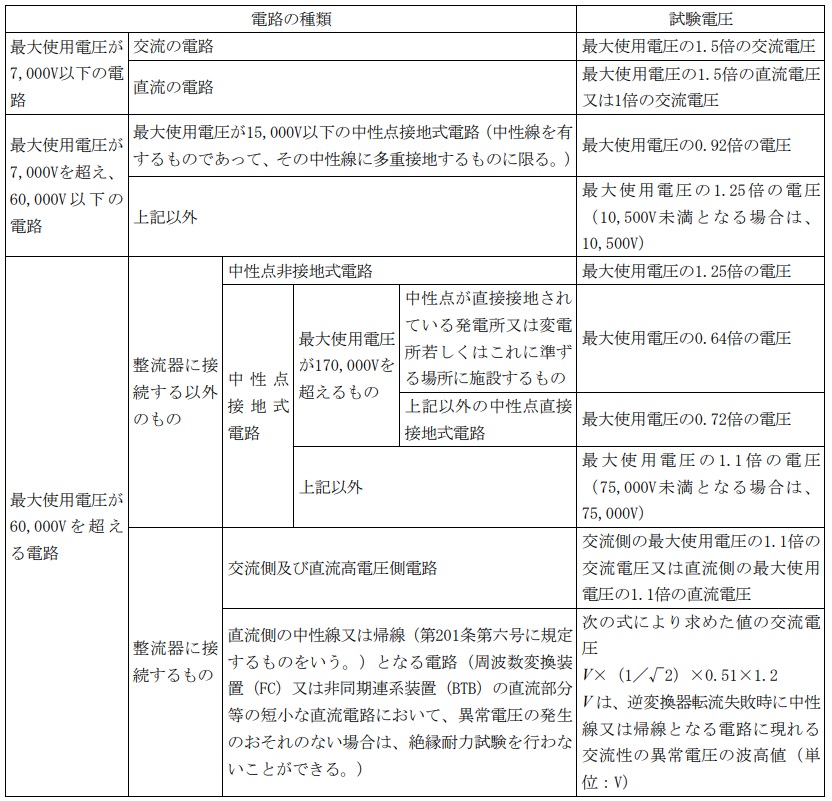
3.ケーブルの試験等価回路
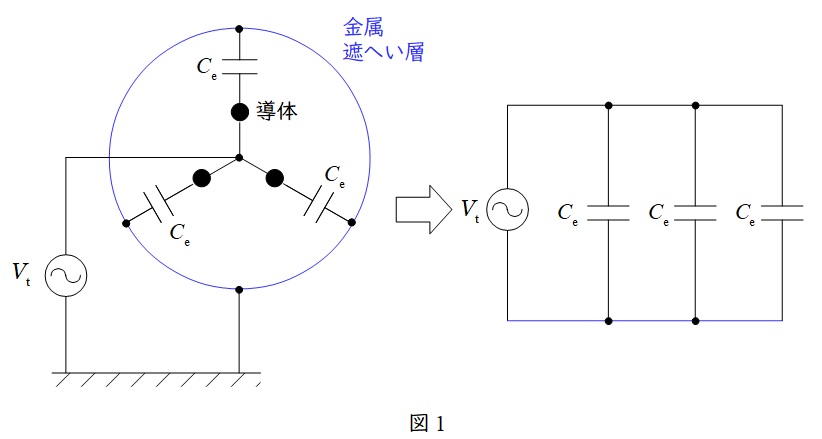
\( \ \mathrm {CVT} \ \)ケーブルの断面図は下図のようになり,各相間および各相と大地との間に静電容量を持ちます。\( \ 3 \ \)線一括の交流絶縁耐力試験では,各相間の静電容量は短絡されるので,静電容量は各相と金属遮へい層の間のみを考慮すればよく,金属遮へい層は接地されているので,等価回路は右図のようになります。
【解答】
(a)解答:(4)
ケーブルの最大使用電圧\( \ E_{\mathrm {m}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {m}}&=&\frac {1.15}{1.1}\times 6600 \\[ 5pt ]
&=&6900 \ \mathrm {[ V ] } \\[ 5pt ]
\end{eqnarray}
\]
となるので,試験電圧\( \ V_{\mathrm {t}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {t}}&=&1.5\times E_{\mathrm {m}} \\[ 5pt ]
&=&1.5\times 6900 \\[ 5pt ]
&=&10350 \ \mathrm {[ V ] } \\[ 5pt ]
\end{eqnarray}
\]
となる。ケーブルの静電容量\( \ C \ \)は,
\[
\begin{eqnarray}
C&=&0.22\times 150\times 10^{-3} \\[ 5pt ]
&=&0.033 \ \mathrm {[ \mu F ] }
\end{eqnarray}
\]
となるので,試験電圧をかけた時に電流計を流れる電流\( \ I \ \)は,三相の並列回路となるから,
\[
\begin{eqnarray}
I&=&\omega \cdot 3C V_{\mathrm {t}} \\[ 5pt ]
&=&2\pi f \cdot 3C V_{\mathrm {t}} \\[ 5pt ]
&=&2\pi \times 50 \times 3 \times 0.033 \times 10^{-6}\times 10350 \\[ 5pt ]
&≒&0.3219 \ \mathrm {[ A ] } → 321.9 \ \mathrm {[ mA ] } \\[ 5pt ]
\end{eqnarray}
\]
となるので,最も近いのは(4)となる。
(b)解答:(1)
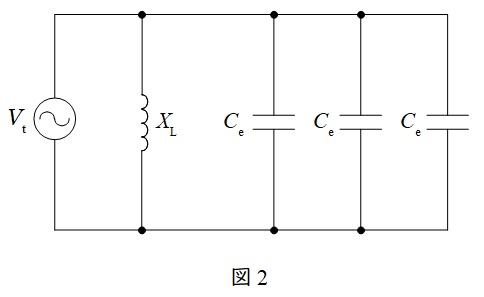
高圧補償リアクトルを含めた試験回路を回路図に描くと図2のようになる。
高圧補償リアクトルの仕様より,高圧補償リアクトルのリアクタンス\( \ X_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {L}}&=&\frac {13\times 10^{3}}{300\times 10^{-3}} \\[ 5pt ]
&≒&43333 \ \mathrm {[\Omega] } \\[ 5pt ]
\end{eqnarray}
\]
となる。高圧補償リアクトルを流れる電流\( \ I_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {L}}&=&\frac {V_{\mathrm {t}}}{X_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {10350}{43333} \\[ 5pt ]
&≒&0.2388 \ \mathrm {[A] } → 238.8 \ \mathrm {[ mA ] } \\[ 5pt ]
\end{eqnarray}
\]
となる。(a)で求めたケーブルを流れる電流\( \ I \ \)は進み無効電流,高圧補償リアクトルを流れる電流\( \ I_{\mathrm {L}} \ \)は遅れ無効電流であるから,変圧器を流れる電流\( \ I_{\mathrm {t}} \ \)は
\[
\begin{eqnarray}
I_{\mathrm {t}}&=&I-I_{\mathrm {L}} \\[ 5pt ]
&=&321.9-238.8 \\[ 5pt ]
&=&83.1 \ \mathrm {[ mA ] } \\[ 5pt ]
\end{eqnarray}
\]
となるので,試験用変圧器の容量\( \ P_{\mathrm {t}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {t}}&=&V_{\mathrm {t}}I_{\mathrm {t}} \\[ 5pt ]
&=&10350\times 83.1\times 10^{-3} \\[ 5pt ]
&≒&860 \ \mathrm {[ V\cdot A ] } → 0.860 \ \mathrm {[ kV\cdot A ] } \\[ 5pt ]
\end{eqnarray}
\]
となり,単相交流発電機に求められる最小の容量は\( \ 1.0 \ \mathrm {[ kV\cdot A ] } \ \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは