Contents
【問題】
【難易度】★★★★☆(やや難しい)
電気事業者から供給を受ける,ある需要家の自家用変電所を送電端とし,高圧三相\( \ 3 \ \)線式\( \ 1 \ \)回線の専用配電線路で受電している第\( \ 2 \ \)工場がある。第\( \ 2 \ \)工場の負荷は\( \ 2000 \ \mathrm {[kW]} \ \),受電電圧は\( \ 6000 \ \mathrm {[V]} \ \)であるとき,第\( \ 2 \ \)工場の力率改善及び受電端電圧の調整を図るため,第\( \ 2 \ \)工場に電力用コンデンサを設置する場合,次の(a)及び(b)の問に答えよ。
ただし,第\( \ 2 \ \)工場の負荷の消費電力及び負荷力率(遅れ)は,受電端電圧によらないものとする。
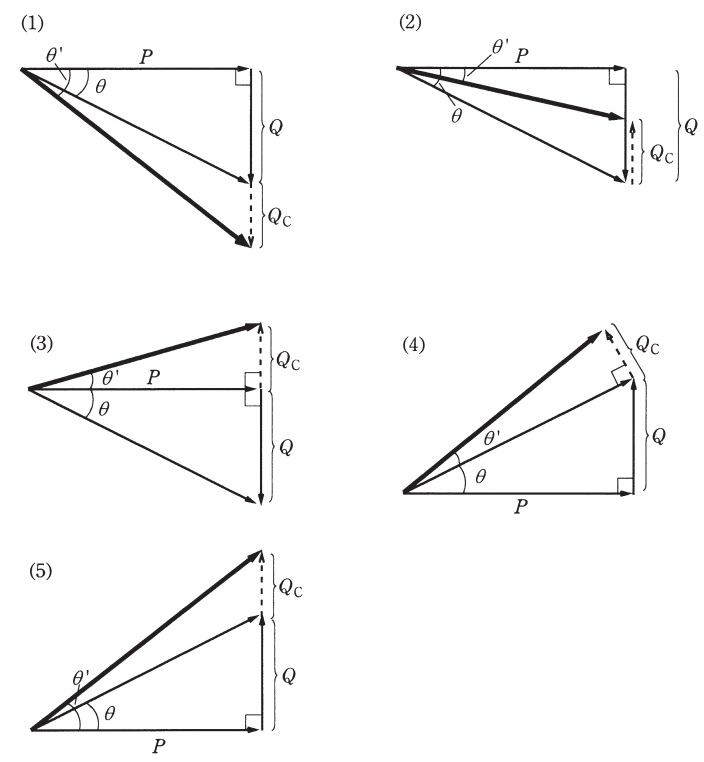
(a) 第\( \ 2 \ \)工場の力率改善のために電力用コンデンサを設置したときの受電端のベクトル図として,正しいものを次の(1)~(5)のうちから一つ選べ。ただし,ベクトル図の文字記号と用語との関係は次のとおりである。
\( \ P \ \) :有効電力\( \ \mathrm {[kW]} \ \)
\( \ Q \ \) :電力用コンデンサ設置前の無効電力\( \ \mathrm {[kvar]} \ \)
\( \ Q_{\mathrm {C}} \ \ \):電力用コンデンサの容量\( \ \mathrm {[kvar]} \ \)
\( \ \theta \ \ \) :電力用コンデンサ設置前の力率角\( \ \mathrm {[°]} \ \)
\( \ \theta ^{\prime }\ \) :電力用コンデンサ設置後の力率角\( \ \mathrm {[°]} \ \)
(b) 第\( \ 2 \ \)工場の受電端電圧を\( \ 6300 \ \mathrm {[V]} \ \)にするために設置する電力用コンデンサ容量は\( \ \mathrm {[kvar]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,自家用変電所の送電端電圧は\( \ 6600 \ \mathrm {[V]} \ \),専用配電線路の電線\( \ 1 \ \)線当たりの抵抗は\( \ 0.5 \ \mathrm {[\Omega ]} \ \)及びリアクタンスは\( \ 1 \ \mathrm {[\Omega ]} \ \)とする。
また,電力用コンデンサ設置前の負荷力率は\( \ 0.6 \ \)(遅れ)とする。
なお,配電線の電圧降下式は,簡略式を用いて計算するものとする。
(1) \( \ 700 \ \) (2) \( \ 900 \ \) (3) \( \ 1500 \ \) (4) \( \ 1800 \ \) (5) \( \ 2000 \ \)
【ワンポイント解説】
力率改善の問題は非常によく出題される内容の一つです。(b)は若干難易度が高い問題ですが,近年難化傾向が強い法規としては,比較的過去問の類題として出題されやすい内容です。電力科目とも重複する内容となりますので,確実に理解しておくようにしましょう。
1.有効電力\( \ P \ \)と無効電力\( \ Q \ \)
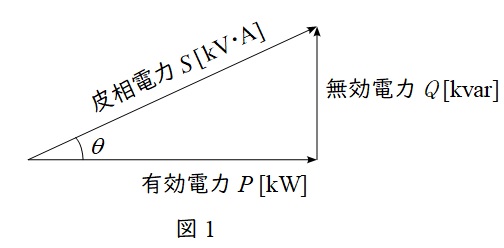
抵抗で消費される電力を有効電力\( \ P \ \)とリアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \)と呼び,図1のようにベクトル図を描きます。さらに,有効電力\( \ P \ \)と無効電力\( \ Q \ \)のベクトル和は皮相電力\( \ S \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図1において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.配電線の電圧降下の近似式
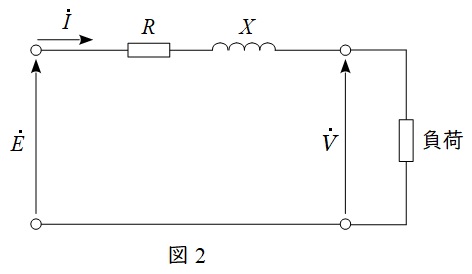
①単相回路の電圧降下
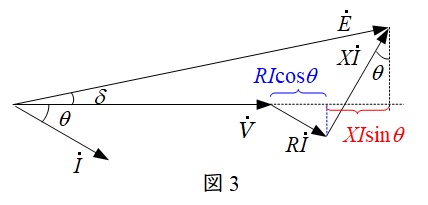
図2のような回路において,ベクトル図を描くと図3のようになります。
図3のベクトル図において,\(\dot E \)と\(\dot V\)の位相差が十分に小さいと仮定すると,線路の電圧降下\( \ \varepsilon =E-V \ \)は,
\[
\begin{eqnarray}
E&≃&V+RI\cos \theta +XI\sin \theta \\[ 5pt ]
E-V&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
\varepsilon &=&I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
②三相\( \ 3 \ \)線式送電線の電圧降下
三相回路においても,一相分の等価回路及びベクトル図は図2及び図3のように描くことができ,三相分の電圧降下\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
※従って本問においては\( \ \sqrt {3} \ \)の計算忘れに注意が必要です。
【解答】
(a)解答:(2)
一般に遅れ力率を正としてベクトル図を描く場合が多いが,本問においてはその指定がない。
第\( \ 2 \ \)工場においては,元々遅れ力率の負荷になっているのを電力用コンデンサにて改善したとなっているので,電力用コンデンサ設置前よりも電力用コンデンサ設置後の方が無効電力が減少していなければならない。
また,電力用コンデンサを設置することによる有効電力は変化がないので,有効電力成分は変化がないことが条件となる。
(1)においては,電力用コンデンサを設置することで,無効電力が増加しているため,誤り。
(2)においては,電力用コンデンサを設置することで,無効電力が減少し,有効電力は変化がないので,正しい。
(3)においては,電力用コンデンサを設置することで,無効電力が減少していることは正しいが,力率改善後の無効電力は\( \ Q-Q_{\mathrm {C}} \ \)とならなければならないので,誤り。
(4)においては,電力用コンデンサを設置することで,無効電力が増加し,有効電力が減少しているため,誤り。
(5)においては,電力用コンデンサを設置することで,無効電力が増加しているため,誤り。
(b)解答:(4)
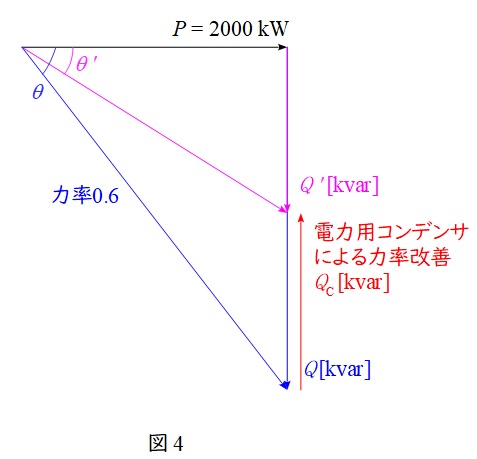
本問の第\( \ 2 \ \)工場における力率改善前後のベクトル図を描くと図4のようになる。
\( \ \cos \theta =0.6 \ \)より,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.6 ^{2}} \\[ 5pt ]
&=&0.8 \\[ 5pt ]
\end{eqnarray}
\]
であるから,力率改善前の無効電力の大きさ\( \ Q \ \)は,
\[
\begin{eqnarray}
Q &=&\frac {P}{\cos \theta }\sin \theta \\[ 5pt ]
&=&\frac {2000}{0.6}\times 0.8 \\[ 5pt ]
&≒&2667 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
ワンポイント解説「2.配電線の電圧降下の近似式」より,電力用コンデンサ接続後の電圧降下\( \ \varepsilon ^{\prime } \ \)は,
\[
\begin{eqnarray}
\varepsilon ^{\prime }&=&\sqrt {3}I^{\prime }\left( R\cos \theta ^{\prime }+X\sin \theta ^{\prime }\right) \\[ 5pt ]
&=&\sqrt {3}RI^{\prime }\cos \theta ^{\prime }+\sqrt {3}XI^{\prime }\sin \theta ^{\prime } ・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
であり,受電端電圧\( \ V_{\mathrm {r}}^{\prime }=6300 \ \mathrm {[V]} \ \),電力用コンデンサ接続後の無効電力の大きさ\( \ Q^{\prime } \ \)とすると,
\[
\begin{eqnarray}
P &=&\sqrt {3}V_{\mathrm {r}}^{\prime }I^{\prime }\cos \theta ^{\prime } \\[ 5pt ]
∴\frac {P}{V_{\mathrm {r}}^{\prime }}&=&\sqrt {3}I^{\prime }\cos \theta ^{\prime } \\[ 5pt ]
Q^{\prime } &=&\sqrt {3}V_{\mathrm {r}}^{\prime }I^{\prime }\sin \theta ^{\prime } \\[ 5pt ]
∴\frac {Q^{\prime }}{V_{\mathrm {r}}^{\prime }}&=&\sqrt {3}I^{\prime }\sin \theta ^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
となり,これを①に代入すると,
\[
\begin{eqnarray}
\varepsilon ^{\prime }&=&R\cdot \frac {P}{V_{\mathrm {r}}^{\prime }}+X\cdot \frac {Q^{\prime }}{V_{\mathrm {r}}^{\prime }} \\[ 5pt ]
V_{\mathrm {r}}^{\prime }\varepsilon ^{\prime }&=&RP+XQ^{\prime } \\[ 5pt ]
XQ^{\prime }&=&V_{\mathrm {r}}^{\prime }\varepsilon ^{\prime }-RP \\[ 5pt ]
Q^{\prime }&=&\frac {V_{\mathrm {r}}^{\prime }\varepsilon ^{\prime }-RP}{X} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入すると,
\[
\begin{eqnarray}
Q^{\prime }&=&\frac {6300\times 300-0.5\times 2000\times 10^{3}}{1} \\[ 5pt ]
&=&890000 \ \mathrm {[var]} → 890 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,電力用コンデンサの容量\( \ Q_{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
Q-Q^{\prime }&=&2667-890 \\[ 5pt ]
&=&1777 → 1800 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは