《電力》〈変電〉[R2:問8]百分率インピーダンスを用いた三相短絡電流の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格容量\( \ 20 \ \mathrm {MV\cdot A} \ \)，一次側定格電圧\( \ 77 \ \mathrm {kV} \ \)，二次側定格電圧\( \ 6.6 \ \mathrm {kV} \ \)，百分率インピーダンス\( \ 10.6 \ \mathrm {％} \ \)（基準容量\( \ 20 \ \mathrm {MV\cdot A} \ \)）の三相変圧器がある。三相変圧器の一次側は\( \ 77 \ \mathrm {kV} \ \)の電源に接続され，二次側は負荷のみが接続されている。三相変圧器の一次側から見た電源の百分率インピーダンスは，\( \ 1.1 \ \mathrm {％} \ \)（基準容量\( \ 20 \ \mathrm {MV\cdot A} \ \)）である。抵抗分及びその他の定数は無視する。三相変圧器の二次側に設置する遮断器の定格遮断電流の値\( \ \mathrm {[kA]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.5 \ \)　　(2)　\( \ 2.6 \ \)　　(3)　\( \ 6.0 \ \)　　(4)　\( \ 20.0 \ \)　　(5)　\( \ 260.0 \ \)

【ワンポイント解説】

三相短絡電流から遮断器の定格遮断電流を求める典型的な百分率インピーダンスを使用する問題ですが，本問は図が与えられていないので，自分で図を描いて計算する能力が求められます。
百分率インピーダンスを苦手にしている受験生も多いですが，定義なので慣れてしまうと弧度法（\( \ \mathrm {rad} \ \)）と同様に使いこなせるようになります。問題演習を繰り返すようにして下さい。

1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \)とすると，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンス容量換算
「1.オーム法からパーセントインピーダンス法への変換」の通り，百分率インピーダンスは基準容量に比例します。したがって，基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の百分率インピーダンスは，
\[
\begin{eqnarray}
％Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}％Z_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.百分率インピーダンスの短絡電流計算
百分率インピーダンスを\( \ ％Z \ \)とすると，三相短絡電流\( \ I_{\mathrm {s}} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{％Z／100} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{Z_{\mathrm {s}}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。

【解答】

解答：(4)
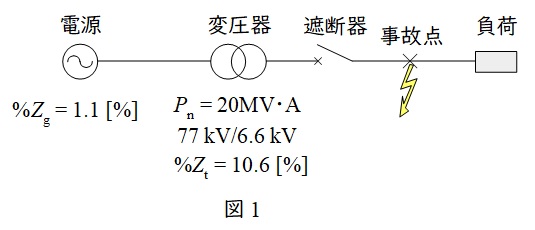
題意に沿って単線結線図を描くと図1のようになる。
図1より，事故点から電源側を見た合成百分率インピーダンス\( \ ％Z \ \)は，電源及び変圧器ともに基準容量が\( \ 20 \ \mathrm {MV\cdot A} \ \)であるから，
\[
\begin{eqnarray}
％Z&=&％Z_{\mathrm {g}}+％Z_{\mathrm {t}} \\[ 5pt ] &=&1.1+10.6 \\[ 5pt ] &=&11.7 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となる。また，二次側の定格電流\( \ I_{\mathrm {n}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {20\times 10^{6}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ] &≒&1749.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「3.百分率インピーダンスの短絡電流計算」より二次側で事故が発生したときの三相短絡電流\( \ I_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] &=&\frac {100\times 1749.5}{11.7} \\[ 5pt ] &≒&14953 \ \mathrm {[A]}　→　15.0 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められ，二次側に設置する遮断器の定格遮断電流として最も適切なのは(4)となる。