【問題】
【難易度】★★★☆☆(普通)
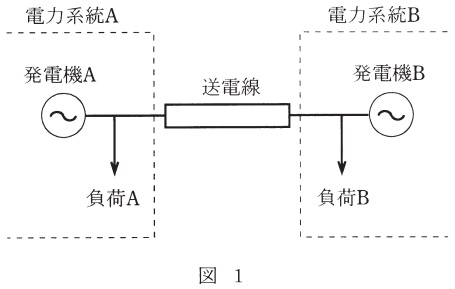
二つの電力系統\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)がある。それぞれの電力系統は図1に示すように,\( \ 1 \ \)発電機,\( \ 1 \ \)負荷で表され,一つの送電線で連系されているものとする。発電機\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)の容量はそれぞれ\( \ 80 \ \mathrm {[MW]} \ \)とし,それぞれの負荷の負荷確率分布は図2に示す折れ線\( \ F\left( L \right) \ \)(負荷電力が\( \ L \ \)を超える確率)であるとする。このとき,電力系統\( \ \mathrm {A} \ \)の電力不足確率(\( \ \mathrm {LOLP} \ \))を,次の場合につき小数第\( \ 3 \ \)位まで求めよ。
(1) 送電線が使用されていない場合。ただし,発電機\( \ \mathrm {A} \ \)の事故停止確率は\( \ \mathrm {0} \ \)とする。
(2) 送電線が使用されていない場合。ただし,発電機\( \ \mathrm {A} \ \)の事故停止確率は\( \ \mathrm {0.02} \ \)とする。
(3) 送電線が使用されている場合。ただし,発電機\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)の事故停止確率はともに\( \ \mathrm {0} \ \)とし,負荷\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)の負荷変動は互いに独立しており,送電線の損失は無視するものとする。
また,電力系統\( \ \mathrm {B} \ \)から電力系統\( \ \mathrm {A} \ \)への電力融通は,次の条件とする。
① 電力系統\( \ \mathrm {A} \ \)の発電電力が電力系統\( \ \mathrm {A} \ \)の負荷電力を下回るとき
② 融通電力は電力系統\( \ \mathrm {B} \ \)の発電電力の余力分まで
③ 送電線の送電容量は\( \ 10 \ \mathrm {[MW]} \ \)
なお,\( \ f\left( L \right) =\displaystyle -\frac {\mathrm {d}F}{\mathrm {d}L} \ \)は確率密度関数と呼ばれ,\( \ f\left( L \right) \mathrm {d}L \ \)は負荷電力が\( \ L~L+\mathrm {d}L \ \)である確率を表し,\( \ F\left( L \right) =1-\int _{0}^{L}f\left( L \right) \mathrm {d}L \ \)の関係がある。

【ワンポイント解説】
電力の系統運用に関する問題です。
\( \ 1 \ \)種に出題される受験生にその場で考えさせる問題の一つと考えて良いです。(1)と(2)が比較的易しい問題なので,時間がないときの部分点狙いとしては良い問題かと思います。
【解答】
(1)送電線が使用されていない場合で発電機\( \ \mathrm {A} \ \)の事故停止確率が\( \ \mathrm {0} \ \)の時の電力不足確率(\( \ \mathrm {LOLP} \ \))
題意より,発電機\( \ \mathrm {A} \ \)が供給可能な電力は\( \ 80 \ \mathrm {[MW]} \ \)なので,負荷需要が\( \ 80 \ \mathrm {[MW]} \ \)を超える場合に電力不足となる。したがって,そのときの電力不足確率\( \ \mathrm {LOLP}_{1} \ \)は,図1より
\[
\begin{eqnarray}
\mathrm {LOLP}_{1}&=&0.250 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)送電線が使用されていない場合で発電機\( \ \mathrm {A} \ \)の事故停止確率が\( \ \mathrm {0.02} \ \)の時の電力不足確率(\( \ \mathrm {LOLP} \ \))
本条件において電力不足が発生するのは,発電機\( \ \mathrm {A} \ \)が通常運転したときの負荷需要が\( \ 80 \ \mathrm {[MW]} \ \)を超えた場合と,発電機\( \ \mathrm {A} \ \)が事故停止したときである。
各確率は,
発電機通常運転確率:\( \ 1-0.02=0.98 \ \)
発電機事故停止確率:\( \ 0.02 \ \)
負荷需要が\( \ 80 \ \mathrm {[MW]} \ \)超確率:\( \ 0.250 \ \)
となるので,電力不足確率\( \ \mathrm {LOLP}_{2} \ \)は,
\[
\begin{eqnarray}
\mathrm {LOLP}_{2}&=&0.98\times 0.250+0.02 \\[ 5pt ]
&=&0.265 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)送電線が使用されている場合の電力不足確率(\( \ \mathrm {LOLP} \ \))
事故停止確率が\( \ \mathrm {0} \ \)であり,送電線の送電容量は\( \ 10 \ \mathrm {[MW]} \ \)であるから,負荷\( \ \mathrm {A} \ \)の需要\( \ L_{\mathrm {A}} \ \)の変化に関してまとめると以下の通りとなる。
\[
\begin{array}{|c|c|c|c|}
\hline
L_{\mathrm {A}} \ \mathrm {[MW]} & 状態 & 発生確率 & 電力不足確率 \\
\hline
0~80 & 供給可能 & 0.75 & 0 \\
80~90 & 系統 \ \mathrm {B} \ による & 0.125 & 詳細計算 \\
90~100 & 電力不足 & 0.125 & 0.125\times 1=0.125 \\
\hline
\end{array}
\]
上表の\( \ 80 ~ 90 \ \mathrm {[MW]} \ \)の間に関して,負荷\( \ \mathrm {B} \ \)の需要\( \ L_{\mathrm {B}} \ \)に対し電力不足となる条件は,
\[
\begin{eqnarray}
80-L_{\mathrm {B}}& < &L_{\mathrm {A}}-80 \\[ 5pt ]
L_{\mathrm {B}}& > &160-L_{\mathrm {A}} ( 80≦L_{\mathrm {A}}≦90 ) \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,上式における電力不足となる\( \ L_{\mathrm {B}} \ \)の条件は,\( \ L_{\mathrm {B}} > 70 \ \)となる。\( \ 80≦L_{\mathrm {A}}≦90 \ \)及び\( \ 70 < L_{\mathrm {B}}≦100 \ \)の時の確率密度関数\( \ f\left( L \right) \ \)は,図2の傾きであるから,
\[
\begin{eqnarray}
f\left( L \right) &=&-\frac {0.00-1.00}{100-20} \\[ 5pt ]
&=&\frac {1}{80} \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より\( \ F\left( L \right) \ \)は,
\[
\begin{eqnarray}
F\left( L \right) &=& 1.00-\int _{20}^{L}f\left( L \right) \mathrm {d}L \\[ 5pt ]
&=& 1.00-\int _{20}^{L}\frac {1}{80} \mathrm {d}L \\[ 5pt ]
&=&1-\left[ \frac {L}{80}\right] _{20}^{L} \\[ 5pt ]
&=&1-\frac {L}{80}+\frac {20}{80} \\[ 5pt ]
&=&\frac {100-L}{80} \\[ 5pt ]
\end{eqnarray}
\]
である。微小区間\( \ L_{\mathrm {B}}~L_{\mathrm {B}}+\mathrm {d}L_{\mathrm {B}} \left( 80≦L_{\mathrm {A}}≦90,70 < L_{\mathrm {B}}≦100 \right) \ \)で電力不足が発生する確率は,
\[
\begin{eqnarray}
f\left( L_{\mathrm {B}} \right) F\left( L_{\mathrm {B}}\right) &=&f\left( L_{\mathrm {B}} \right) F\left( 160-L_{\mathrm {A}} \right) \\[ 5pt ]
&=& \frac {1}{80}\times \frac {100-\left( 160-L_{\mathrm {A}} \right) }{80} \\[ 5pt ]
&=& \frac {L_{\mathrm {A}}-60 }{6400} \\[ 5pt ]
\end{eqnarray}
\]
となるので両辺積分すると,
\[
\begin{eqnarray}
\int _{80}^{90} f\left( L_{\mathrm {B}} \right) F\left( 160-L_{\mathrm {A}} \right) \mathrm {d}L_{\mathrm {A}} &=&\int _{80}^{90} \frac {L_{\mathrm {A}}-60 }{6400} \mathrm {d}L_{\mathrm {A}} \\[ 5pt ]
&=&\frac {1}{6400}\int _{80}^{90} \left( L_{\mathrm {A}}-60 \right) \mathrm {d}L_{\mathrm {A}} \\[ 5pt ]
&=&\frac {1}{6400}\left[ \frac {L_{\mathrm {A}}^{2}}{2}-60L_{\mathrm {A}}\right] _{80}^{90} \\[ 5pt ]
&=&\frac {1}{6400}\left( \frac {8100}{2}-5400-\frac {6400}{2}+4800\right) \\[ 5pt ]
&≒&0.039063 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。以上から,送電線が使用されている場合の電力不足確率\( \ \mathrm {LOLP}_{3} \ \)は,
\[
\begin{eqnarray}
\mathrm {LOLP}_{3} &=&0+0.039063+0.125 \\[ 5pt ]
&≒&0.164 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん